AP Precalculus -2.2 Linear and Exponential Change- Study Notes - Effective Fall 2023
AP Precalculus -2.2 Linear and Exponential Change- Study Notes – Effective Fall 2023
AP Precalculus -2.2 Linear and Exponential Change- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Construct functions of the real numbers that are comparable to arithmetic and geometric sequences
Describe similarities and differences between linear and exponential functions.
Key Concepts:
Connection Between Linear Functions and Arithmetic Sequences
Point–Slope Form and Its Connection to Arithmetic Sequences
Connection Between Exponential Functions and Geometric Sequences
Point-Based Form of Exponential Functions and Its Connection to Geometric Sequences
Domains of Sequences and Their Corresponding Functions
Identifying Linear vs Exponential Change Over Equal Intervals
Comparing Linear and Exponential Functions
Determining Sequences and Functions from Two Values
Connection Between Linear Functions and Arithmetic Sequences
Linear functions and arithmetic sequences are closely related because both are built from an initial value plus repeated addition of a constant rate of change.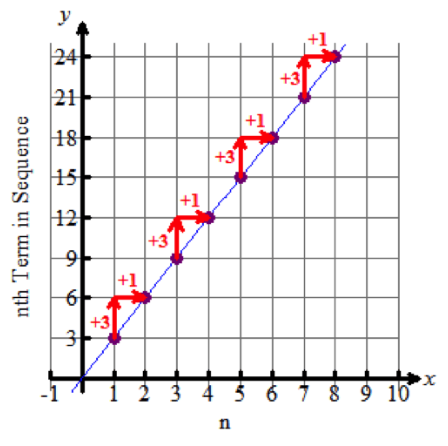
A linear function can be written as
\( \mathrm{ \displaystyle f(x) = b + mx } \)
where \( \mathrm{b} \) is the initial value and \( \mathrm{m} \) is the constant rate of change (slope).
An arithmetic sequence can be written as
\( \mathrm{ \displaystyle a_n = a_0 + dn } \)
where \( \mathrm{a_0} \) is the initial value and \( \mathrm{d} \) is the common difference.
In both forms:
• The output starts from an initial value
• Each step adds the same constant amount
The key difference is that a linear function is defined for all real input values, while an arithmetic sequence is defined only for whole-number inputs.
Example
Consider the linear function
\( \mathrm{ \displaystyle f(x) = 5 + 3x } \)
Write the corresponding arithmetic sequence.
▶️ Answer/Explanation
The initial value is \( \mathrm{5} \), and the constant rate of change is \( \mathrm{3} \).
The arithmetic sequence is
\( \mathrm{ \displaystyle a_n = 5 + 3n } \)
The terms are \( \mathrm{5, 8, 11, 14, \dots} \).
Conclusion
The arithmetic sequence mirrors the linear function at whole-number input values.
Example
An arithmetic sequence is defined by
\( \mathrm{ \displaystyle a_n = 10 + 4n } \)
Write the equivalent linear function.
▶️ Answer/Explanation
The initial value is \( \mathrm{10} \), and the common difference is \( \mathrm{4} \).
The corresponding linear function is
\( \mathrm{ \displaystyle f(x) = 10 + 4x } \)
Conclusion
The arithmetic sequence is the discrete version of the linear function.
Point–Slope Form and Its Connection to Arithmetic Sequences
Arithmetic sequences and linear functions can both be written using a known rate of change and a known value.
An arithmetic sequence based on a known term \( \mathrm{a_k} \) and common difference \( \mathrm{d} \) can be written as
\( \mathrm{ \displaystyle a_n = a_k + d(n – k) } \)
This formula starts at the known term and adds the common difference repeatedly to reach other terms.
In a similar way, a linear function can be written using a known point and a known slope.
If a linear function has slope \( \mathrm{m} \) and passes through the point \( \mathrm{(x_i, y_i)} \), it can be written in point–slope form as
\( \mathrm{ \displaystyle f(x) = y_i + m(x – x_i) } \)
This form emphasizes how output values change starting from a known point and increasing or decreasing at a constant rate.
Just as arithmetic sequences extend values step by step, point–slope form extends a linear relationship across all real input values.
Example
An arithmetic sequence has a common difference of \( \mathrm{d = 5} \) and the 4th term is \( \mathrm{a_4 = 12} \).
Write a formula for \( \mathrm{a_n} \).
▶️ Answer/Explanation
Use the known-term form:
\( \mathrm{ \displaystyle a_n = a_4 + 5(n – 4) } \)
Substitute the value of \( \mathrm{a_4} \):
\( \mathrm{ \displaystyle a_n = 12 + 5(n – 4) } \)
Conclusion
The sequence is built from the 4th term by adding the common difference.
Example
A linear function has slope \( \mathrm{m = 3} \) and passes through the point \( \mathrm{(2, 7)} \).
Write the equation of the line using point–slope form.
▶️ Answer/Explanation
Use the point–slope formula:
\( \mathrm{ \displaystyle f(x) = 7 + 3(x – 2) } \)
This equation starts at the known point and increases at a constant rate of 3.
Conclusion
Point–slope form plays the same role for linear functions that the known-term formula plays for arithmetic sequences.
Connection Between Exponential Functions and Geometric Sequences
Exponential functions and geometric sequences are closely related because both are built from an initial value multiplied repeatedly by a constant proportion.
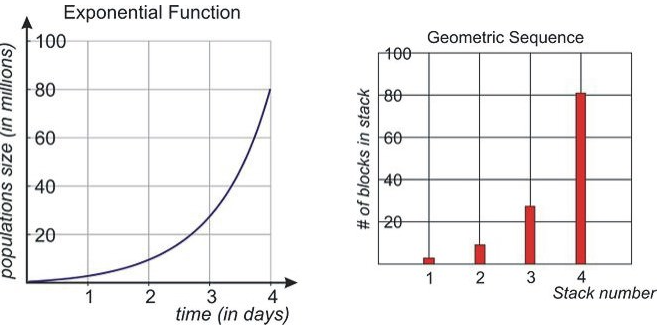
An exponential function can be written as
\( \mathrm{ \displaystyle f(x) = a b^x } \)
where \( \mathrm{a} \) is the initial value and \( \mathrm{b} \) is the constant growth or decay factor.
A geometric sequence can be written as
\( \mathrm{ \displaystyle g_n = g_0 r^n } \)
where \( \mathrm{g_0} \) is the initial value and \( \mathrm{r} \) is the common ratio.
In both cases:
• The process starts with an initial value
• Each step multiplies by the same constant factor
The key difference is that exponential functions are defined for all real input values, while geometric sequences are defined only for whole-number inputs.
Thus, a geometric sequence can be viewed as the discrete version of an exponential function.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = 3 \cdot 2^x } \)
Write the corresponding geometric sequence.
▶️ Answer/Explanation
The initial value is \( \mathrm{3} \), and the constant factor is \( \mathrm{2} \).
The corresponding geometric sequence is
\( \mathrm{ \displaystyle g_n = 3 \cdot 2^n } \)
The terms are \( \mathrm{3, 6, 12, 24, \dots} \).
Conclusion
The geometric sequence matches the exponential function at whole-number inputs.
Example
A geometric sequence is defined by
\( \mathrm{ \displaystyle g_n = 5(0.8)^n } \)
Write the corresponding exponential function.
▶️ Answer/Explanation
The initial value is \( \mathrm{5} \), and the common ratio is \( \mathrm{0.8} \).
The corresponding exponential function is
\( \mathrm{ \displaystyle f(x) = 5(0.8)^x } \)
Conclusion
The exponential function is the continuous version of the geometric sequence.
Point-Based Form of Exponential Functions and Its Connection to Geometric Sequences
Geometric sequences and exponential functions can both be written using a known ratio and a known value.
A geometric sequence based on a known term \( \mathrm{g_k} \) and common ratio \( \mathrm{r} \) can be written as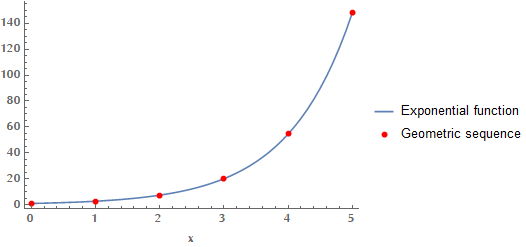
\( \mathrm{ \displaystyle g_n = g_k r^{(n-k)} } \)
This formula starts at the known term and repeatedly multiplies by the constant ratio to generate other terms.
In a similar way, an exponential function can be written using a known point and a known ratio.
If an exponential function has constant ratio \( \mathrm{r} \) and passes through the point \( \mathrm{(x_i, y_i)} \), it can be written as
\( \mathrm{ \displaystyle f(x) = y_i r^{(x – x_i)} } \)
This form emphasizes how the output values change multiplicatively starting from a known point.
Just as the known-term form extends a geometric sequence step by step, this point-based form extends an exponential relationship across all real input values.
Example
A geometric sequence has common ratio \( \mathrm{r = 2} \) and the 3rd term is \( \mathrm{g_3 = 10} \).
Write a formula for \( \mathrm{g_n} \).
▶️ Answer/Explanation
Use the known-term form:
\( \mathrm{ \displaystyle g_n = g_3 \cdot 2^{(n-3)} } \)
Substitute \( \mathrm{g_3 = 10} \):
\( \mathrm{ \displaystyle g_n = 10 \cdot 2^{(n-3)} } \)
Conclusion
The sequence is generated by multiplying by 2 as the index increases.
Example
An exponential function has constant ratio \( \mathrm{r = 2} \) and passes through the point \( \mathrm{(3, 10)} \).
Write the equation of the function.
▶️ Answer/Explanation
Use the point-based exponential form:
\( \mathrm{ \displaystyle f(x) = 10 \cdot 2^{(x – 3)} } \)
This formula starts at the known point and multiplies by 2 for each increase of 1 in \( \mathrm{x} \).
Conclusion
The point-based form of an exponential function plays the same role as the known-term form of a geometric sequence.
Domains of Sequences and Their Corresponding Functions
Although sequences and their corresponding functions may share the same formula, they often have different domains.
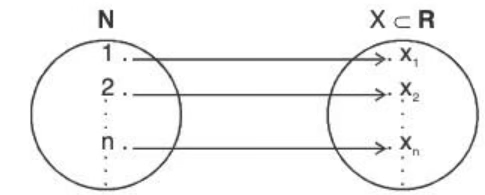
A sequence is defined only for whole-number inputs, usually \( \mathrm{n = 0, 1, 2, 3, \dots} \).
A corresponding function is typically defined for all real input values in an interval.
As a result, a sequence produces a discrete set of points, while the corresponding function produces a continuous graph.
Even when the same expression is used, the interpretation depends on whether the input variable represents an index or a real-valued quantity.
Summary
• Sequences: domain is whole numbers
• Functions: domain is real numbers
Example
Consider the geometric sequence defined by
\( \mathrm{ \displaystyle g_n = 2^n } \)
Describe its domain and compare it to the corresponding exponential function.
▶️ Answer/Explanation
Sequence domain
The sequence is defined only for \( \mathrm{n = 0, 1, 2, 3, \dots} \).
Corresponding function
The corresponding function is
\( \mathrm{ \displaystyle f(x) = 2^x } \)
This function is defined for all real values of \( \mathrm{x} \).
Conclusion
The sequence consists of discrete points, while the function forms a continuous curve.
Example
An arithmetic sequence is defined by
\( \mathrm{ \displaystyle a_n = 4n + 1 } \)
Compare it with the corresponding linear function.
▶️ Answer/Explanation
The sequence is defined only for whole-number values of \( \mathrm{n} \).
The corresponding linear function is
\( \mathrm{ \displaystyle f(x) = 4x + 1 } \)
This function is defined for all real values of \( \mathrm{x} \).
Conclusion
Even though the formulas match, the domains are different.
Identifying Linear vs Exponential Change Over Equal Intervals
The behavior of a function over equal-length input-value intervals can be used to determine whether the function is linear or exponential.
If the output values change by a constant amount over equal input intervals, the function is linear.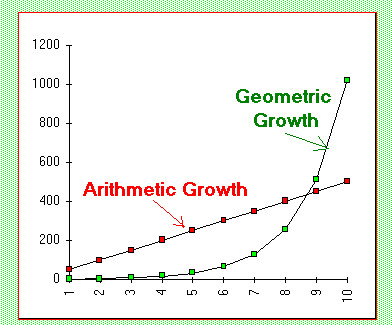
Mathematically, this means
\( \mathrm{ \displaystyle f(x+h) – f(x) = \text{constant} } \)
In contrast, if the output values change by a constant ratio over equal input intervals, the function is exponential.
Mathematically, this means
\( \mathrm{ \displaystyle \dfrac{f(x+h)}{f(x)} = \text{constant} } \)
Thus, linear functions model constant additive change, while exponential functions model constant proportional change.
Key Comparison
• Linear: equal differences → straight-line behavior
• Exponential: equal ratios → curved growth or decay
Example
A function has the following output values:
\( \mathrm{ f(1)=4,\; f(2)=7,\; f(3)=10,\; f(4)=13 } \)
Determine whether the function is linear or exponential.
▶️ Answer/Explanation
Compute successive differences:
\( \mathrm{ 7-4=3 } \)
\( \mathrm{ 10-7=3 } \)
\( \mathrm{ 13-10=3 } \)
The output changes by a constant amount.
Conclusion
The function is linear.
Example
A function has the following output values:
\( \mathrm{ f(1)=5,\; f(2)=10,\; f(3)=20,\; f(4)=40 } \)
Determine whether the function is linear or exponential.
▶️ Answer/Explanation
Compute successive ratios:
\( \mathrm{ 10\div5=2 } \)
\( \mathrm{ 20\div10=2 } \)
\( \mathrm{ 40\div20=2 } \)
The output values change proportionally.
Conclusion
The function is exponential.
Comparing Linear and Exponential Functions
Both linear and exponential functions can be expressed analytically using an initial value and a constant that describes how change occurs.
A linear function can be written as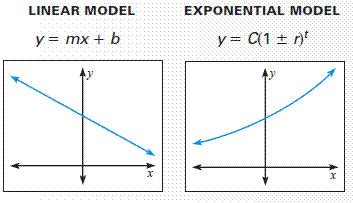
\( \mathrm{ \displaystyle f(x) = mx + b } \)
where \( \mathrm{b} \) is the initial value and \( \mathrm{m} \) is the constant rate of change.
An exponential function can be written as
\( \mathrm{ \displaystyle f(x) = ab^x } \)
where \( \mathrm{a} \) is the initial value and \( \mathrm{b} \) is the constant growth or decay factor.
Although both forms involve an initial value and a constant associated with change, the type of change is different.
Key Difference
• Linear functions are based on addition of a constant amount
• Exponential functions are based on multiplication by a constant factor
This fundamental difference explains why linear graphs are straight lines, while exponential graphs are curved.
Example
A function increases by 5 units each time the input increases by 1.
Identify the type of function.
▶️ Answer/Explanation
The output increases by the same amount each time.
This indicates additive change.
Conclusion
The function is linear.
Example
A function doubles each time the input increases by 1.
Identify the type of function.
▶️ Answer/Explanation
The output is multiplied by 2 for each increase of 1 in the input.
This indicates multiplicative change.
Conclusion
The function is exponential.
Determining Sequences and Functions from Two Values
Arithmetic sequences, linear functions, geometric sequences, and exponential functions share an important property.
Each of these can be uniquely determined using two distinct values, provided the values correspond to different inputs.
This is because each structure depends on a constant type of change:
• Arithmetic sequences and linear functions depend on a constant difference
• Geometric sequences and exponential functions depend on a constant ratio
Knowing two distinct values allows the constant difference or ratio to be calculated, which completely determines the sequence or function.
This is why:
• Two points determine a line
• Two terms determine an arithmetic or geometric sequence
Example
An arithmetic sequence has terms \( \mathrm{a_2 = 7} \) and \( \mathrm{a_5 = 19} \).
Determine the sequence.
▶️ Answer/Explanation
Compute the common difference:
\( \mathrm{ \displaystyle d = \dfrac{19 – 7}{5 – 2} = 4 } \)
Use the known-term formula:
\( \mathrm{ \displaystyle a_n = 7 + 4(n – 2) } \)
Conclusion
Two terms are sufficient to determine the entire arithmetic sequence.
Example
An exponential function passes through the points \( \mathrm{(1, 6)} \) and \( \mathrm{(4, 48)} \).
Determine the function.
▶️ Answer/Explanation
Assume the form
\( \mathrm{ \displaystyle f(x) = ab^x } \)
Use the two points to find the ratio:
\( \mathrm{ \displaystyle \dfrac{48}{6} = b^{4-1} = b^3 } \)
So \( \mathrm{b = 2} \).
Substitute to find \( \mathrm{a} \):
\( \mathrm{ \displaystyle 6 = a \cdot 2^1 } \Rightarrow a = 3 \)
Conclusion
Two distinct points are enough to determine an exponential function.
