AP Precalculus -2.3 Exponential Functions- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -2.3 Exponential Functions- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -2.3 Exponential Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The value $ 2 \cdot 2 \cdot 2 \cdot 2 \cdot 4.7 $ is the output value of an exponential function of the form $ f(x) = a \cdot b^x $, where $ a $ and $ b $ are constants. Which of the following describes the function and input value that corresponds to this output value?

(A) The exponential function has an initial value of 1 and a base of $ 2 \cdot 4.7 $, and the input value is 5.
(B) The exponential function has an initial value of 2 and a base of 2, and the input value is 4.7.
(C) The exponential function has an initial value of 4.7 and a base of 2, and the input value is 4.7.
(D) The exponential function has an initial value of 4.7 and a base of 2, and the input value is 5.

▶️ Answer/Explanation

Detailed solution

Given output value:
$
2 \cdot 2 \cdot 2 \cdot 2 \cdot 4.7
$

Step 1: Rewrite in exponential form
$
2 \cdot 2 \cdot 2 \cdot 2 \cdot 4.7 = 4.7 \cdot 2^4
$

Step 2: Compare with the exponential form
$
f(x) = a \cdot b^x
$

Comparing,
$
a = 4.7,\quad b = 2,\quad x = 4
$

Step 3: Match with the given options

The exponential function has initial value $4.7$ and base $2$.

$
\boxed{\text{Correct answer: (D)}}
$

Question

The function $ f $ is given by $ f(x) = 5 \cdot (0.7)^x $. Which of the following describes $ f $?

(A) The function $ f $ models exponential decay and $ \lim_{x \to \infty} f(x) = 0 $.
(B) The function $ f $ models exponential decay and $ \lim_{x \to -\infty} f(x) = \infty $.
(C) The function $ f $ models exponential growth and $ \lim_{x \to -\infty} f(x) = 0 $.
(D) The function $ f $ models exponential growth and $ \lim_{x \to \infty} f(x) = \infty $.

▶️ Answer/Explanation

Detailed solution

Base $ b = 0.7 $, which is between 0 and 1 ⇒ exponential decay.
As $ x \to \infty $, $ (0.7)^x \to 0 $ ⇒ $ f(x) \to 0 $.
As $ x \to -\infty $, $ (0.7)^x \to \infty $ ⇒ $ f(x) \to \infty $.
Option (A) matches decay and limit 0 at $ +\infty $.
✅ Answer: (A)

Question

The exponential function $ f $ is defined by $ f(x) = ab^x $, where $ a $ and $ b $ are positive constants. The table gives values of $ f(x) $ at selected values of $ x $. Which of the following statements is true?

\[ \begin{array}{c|ccccc} x & 0 & 1 & 2 & 3 & 4 \\ \hline f(x) & \frac{3}{4} & \frac{3}{2} & 3 & 6 & 12 \\ \end{array} \]
(A) $ f $ demonstrates exponential decay because $ a > 0 $ and $ 0 0 $ and $ b > 1 $.
(C) $ f $ demonstrates exponential growth because $ a > 0 $ and $ 0 0 $ and $ b > 1 $.

▶️ Answer/Explanation

Detailed solution

From the table: $ f(0) = a = \frac{3}{4} > 0 $.
$ f(1) = ab = \frac{3}{2} $ ⇒ $ b = \frac{3/2}{3/4} = 2 $.
Since $ b = 2 > 1 $, $ f $ shows exponential growth.
✅ Answer: (D)

Question

The table gives values of the function $ f $ for selected values of $ x $. Which of the following expressions could define $ f(x) $?

\[ \begin{array}{c|cccc} x & 0 & 2 & 4 & 6 \\ \hline f(x) & 3 & 48 & 768 & 12{,}288 \\ \end{array} \]
(A) $ 2 + 4^x $
(B) $ 3 \cdot 4^x $
(C) $ 3 \cdot 16^x $
(D) $ 4 \cdot 3^x $

▶️ Answer/Explanation

Detailed solution

Check $ x=0 $: $ f(0) = 3 $, so $ a = 3 $ if $ f(x) = a \cdot b^x $.
Now check ratios: $ \frac{f(2)}{f(0)} = \frac{48}{3} = 16 $ ⇒ $ b^2 = 16 $ ⇒ $ b = 4 $ or $ -4 $ (positive base) ⇒ $ b=4 $.
Verify: $ 3 \cdot 4^2 = 3 \cdot 16 = 48 $ ✔
$ 3 \cdot 4^4 = 3 \cdot 256 = 768 $ ✔
$ 3 \cdot 4^6 = 3 \cdot 4096 = 12{,}288 $ ✔
Thus $ f(x) = 3 \cdot 4^x $.
✅ Answer: (B)

Question

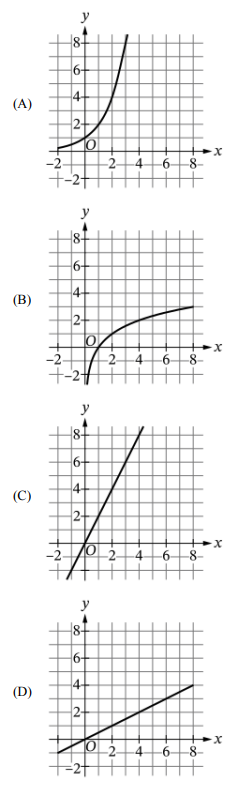
The function $ g $ has the property that for each time the input values double, the output values increase by 1. Which of the following could be the graph of $ y = g(x) $ in the $ xy $-plane?

▶️ Answer/Explanation

Detailed solution

The property “when input doubles, output increases by 1” is characteristic of a logarithmic function with base 2: $ g(x) = \log_2 x $.
This function satisfies $ g(2x) = g(x) + 1 $.
Graphically, it is increasing, passes through (1,0), (2,1), (4,2), etc., with a vertical asymptote at $ x=0 $.
✅ Answer: (B)

Question

An exponential function $ G $ has a known common ratio of $\frac{1}{2}$ and includes the input-output pair $(1,4)$. Which of the following could define $ G(x) $?

(A) $ 4 + \frac{1}{2}(x – 1) $
(B) $ \frac{1}{2} \cdot 4^x $
(C) $ 4 \cdot \left( \frac{1}{2} \right)^x $
(D) $ 4 \cdot \left( \frac{1}{2} \right)^{(x-1)} $

▶️ Answer/Explanation

Detailed solution

Common ratio $ \frac{1}{2} $ means each term is multiplied by $ \frac{1}{2} $. Given $ G(1) = 4 $, we can write the exponential function in the form $ G(x) = a \cdot \left(\frac{1}{2}\right)^{x-k} $ where $ k $ is a shift.
Test (D): $ G(x) = 4 \cdot \left(\frac{1}{2}\right)^{(x-1)} $. Check $ x = 1 $: $ G(1) = 4 \cdot \left(\frac{1}{2}\right)^{0} = 4 $ ✅.
Check ratio: $ G(x+1) / G(x) = \frac{4 \cdot (1/2)^{x}}{4 \cdot (1/2)^{x-1}} = \frac{1}{2} $ ✅.
✅ Answer: (D)

Question

Consider the functions $g$ and $h$ given by $g(x)=4^{x}$ and $h(x)=16^{x+2}$. In the $xy$-plane, what is the $x$-coordinate of the point of intersection of the graphs of $g$ and $h$?

(A) $-4$
(B) $-2$
(C) $0$
(D) $2$

▶️ Answer/Explanation

Detailed solution

1. Set the functions equal:
To find the intersection, equate $g(x)$ and $h(x)$:
$4^{x} = 16^{x+2}$

2. Express with a common base:
Since $16 = 4^2$, substitute this into the equation:
$4^{x} = (4^2)^{x+2}$

3. Solve for $x$:
$4^{x} = 4^{2(x+2)}$
$x = 2x + 4$
$-x = 4 \implies x = -4$

✅ Answer: (A)

Question

Which of the following statements is true about the exponential function $h$ given by $h(x)=-3\cdot4^{x}$?

(A) $h$ is always increasing, and the graph of $h$ is always concave up.
(B) $h$ is always increasing, and the graph of $h$ is always concave down.
(C) $h$ is always decreasing, and the graph of $h$ is always concave up.
(D) $h$ is always decreasing, and the graph of $h$ is always concave down.

▶️ Answer/Explanation

Detailed solution

1. Analyze the parent function $4^x$:
$4^x$ is increasing and concave up (growth).

2. Analyze the transformation:
Multiplication by $-3$ reflects the graph over the $x$-axis.

3. Determine new behavior:
Reflection changes “increasing” to “decreasing” and “concave up” to “concave down”.

✅ Answer: (D)

Question

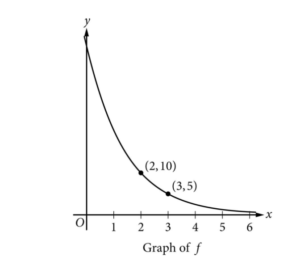
The figure shows the graph of an exponential decay function $f$. The coordinates of two of the points are labeled as $(2, 10)$ and $(3, 5)$. If $y=f(x)$, what is the $y$-coordinate of the point on the graph where $x=0$?

(A) $40$
(B) $30$
(C) $20$
(D) $15$

▶️ Answer/Explanation

Detailed solution

1. Determine Decay Factor:
Moving from $x=2$ to $x=3$, $y$ changes from $10$ to $5$.
Ratio = $5/10 = 1/2$.

2. Work Backward to $x=0$:
At $x=1$: $y = 10 \div (1/2) = 20$.
At $x=0$: $y = 20 \div (1/2) = 40$.

✅ Answer: (A)

Question

The exponential function $f$ is defined by $f(x) = ab^x$, where $a$ and $b$ are positive constants. The table gives values of $f(x)$ at selected values of $x$. Which of the following statements is true?

(A) $f$ demonstrates exponential decay because $a > 0$ and $0 0$ and $b > 1$.
(C) $f$ demonstrates exponential growth because $a > 0$ and $0 0$ and $b > 1$.

▶️ Answer/Explanation

Detailed solution

From the table:
\[ f(0) = ab^0 = a = \frac{3}{4} \]
\[ f(1) = ab^1 = \frac{3}{4} b = \frac{3}{2} \quad\Rightarrow\quad b = 2 \]
Check further: $ f(2) = \frac{3}{4} \cdot 2^2 = 3 $, $ f(3) = \frac{3}{4} \cdot 2^3 = 6 $, $ f(4) = \frac{3}{4} \cdot 2^4 = 12 $, consistent.
So $ a = \frac{3}{4} > 0 $, $ b = 2 > 1 $.
Since $ b > 1 $, the function shows exponential growth.
✅ Answer: (D)

Question

Above is the graph of $f(x)$, an exponential function. Which one of the following best represents the graph of $f(x)$?

a. $y = -2 \cdot 2^{x+2} – 1$

b. $y = -2 \cdot 2^{x+1} + 1$

c. $y = -2 \cdot 2^{x-1} + 1$

d. $y = -2 \cdot 2^{x-2} + 1$

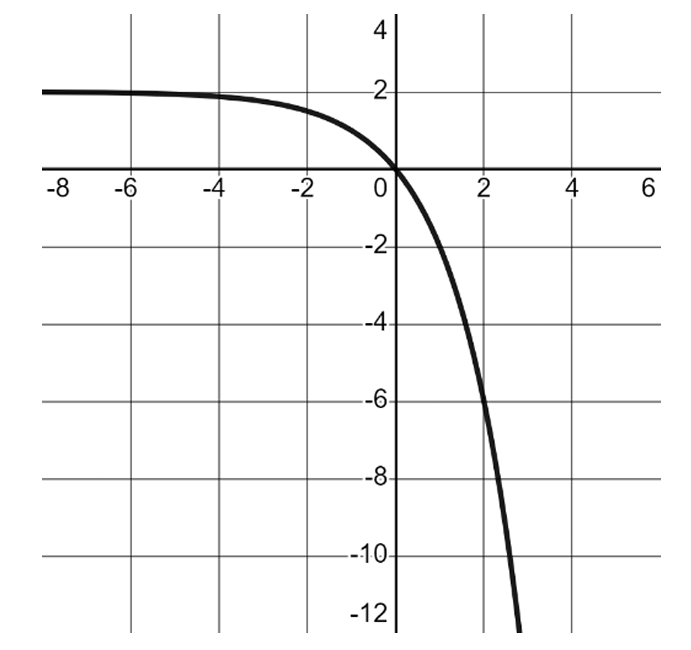
▶️ Answer/Explanation

Detailed solution

The graph shows a horizontal asymptote at $y = 2$, which does not match any given option exactly.
However, testing the $y$-intercept $(0, 0)$ is the most efficient way to identify the intended equation.
For option (b): $y = -2 \cdot 2^{0+1} + 1 = -2 \cdot 2 + 1 = -3$ (Incorrect).
For option (c): $y = -2 \cdot 2^{0-1} + 1 = -2 \cdot 2^{-1} + 1 = -2 \cdot \frac{1}{2} + 1 = 0$ (Correct).
The point $(0, 0)$ lies exactly on the graph, confirming the function’s behavior.
Option (c) also correctly shows a downward-opening exponential curve consistent with the visual trend.
Therefore, the best representation of the graph is option c.

Question

The function $f$ is given by $f(x)=4\left(\frac{2}{3}\right)^x$. Which of the following describes the end behavior of $f$?

(A) $\lim_{x\to-\infty} f(x) = -\infty \text{ and } \lim_{x\to\infty} f(x) = \infty$

(B) $\lim_{x\to-\infty} f(x) = \infty \text{ and } \lim_{x\to\infty} f(x) = -\infty$

(D) $\lim_{x\to-\infty} f(x) = \infty \text{ and } \lim_{x\to\infty} f(x) = 0$

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

The function is given by $f(x) = 4(\frac{2}{3})^x$, which is in the form $a \cdot b^x$.
Here, the base is $b = \frac{2}{3}$. Since $0 < b < 1$, $f(x)$ is an exponential decay function.
As $x \to \infty$, the term $(\frac{2}{3})^x$ approaches $0$, so $\lim_{x\to\infty} f(x) = 0$.
As $x \to -\infty$, the term $(\frac{2}{3})^x$ grows without bound (approaches $\infty$), so $\lim_{x\to-\infty} f(x) = \infty$.
Therefore, the end behavior is described by $\lim_{x\to-\infty} f(x) = \infty$ and $\lim_{x\to\infty} f(x) = 0$.

Question

The function $ g $ is given by $ g(x) = 2(3)^x $. Which of the following describes the end behavior of $ g $?

(A) $ \lim_{x\to-\infty} g(x)=0 $ and $ \lim_{x\to\infty} g(x)=-\infty $

(B) $ \lim_{x\to-\infty} g(x)=-\infty $ and $ \lim_{x\to\infty} g(x)=0 $

(D) $ \lim_{x\to-\infty} g(x)=\infty $ and $ \lim_{x\to\infty} g(x)=0 $

▶️ Answer/Explanation

Detailed solution

The given function is $ g(x) = 2(3)^x $, which is an exponential function of the form $ y = ab^x $.
Here, the base is $ b = 3 $. Since $ b > 1 $, the function represents exponential growth.
As $ x \to \infty $ (as x gets larger), the value of $ 3^x $ increases without bound, so $ \lim_{x\to\infty} g(x)=\infty $.
As $ x \to -\infty $ (as x gets smaller), the value of $ 3^x $ approaches 0, so $ \lim_{x\to-\infty} g(x)=0 $.
Therefore, the end behavior is defined by a limit of 0 on the left and $ \infty $ on the right.
Correct Answer: (C)

Question

The function $ h $ is given by $ h(x) = \frac{2}{5}(4)^x $. Which of the following describes the end behavior of $ h $?

(A) $ \lim_{x\to-\infty} h(x) = 0 $ and $ \lim_{x\to\infty} h(x) = -\infty $

(B) $ \lim_{x\to-\infty} h(x) = -\infty $ and $ \lim_{x\to\infty} h(x) = 0 $

(D) $ \lim_{x\to-\infty} h(x) = \infty $ and $ \lim_{x\to\infty} h(x) = 0 $

▶️ Answer/Explanation

Detailed solution

The function is defined as $ h(x) = \frac{2}{5}(4)^x $.
Identify the base of the exponent: here, $ b = 4 $.
Since the base $ b > 1 $, the function represents exponential growth.
Consider the limit as $ x \to \infty $: As $ x $ gets larger, $ 4^x $ increases without bound, so $ \lim_{x\to\infty} h(x) = \infty $.
Consider the limit as $ x \to -\infty $: As $ x $ becomes a large negative number, $ 4^x $ approaches $ 0 $, so $ \lim_{x\to-\infty} h(x) = 0 $.
Therefore, the end behavior corresponds to Option (C).

Question

The function $ k $ is given by $ k(x) = -3(5)^x $. Which of the following describes the end behavior of $ k $?

(A) $ \lim_{x\to-\infty} k(x) = 0 $ and $ \lim_{x\to\infty} k(x) = -\infty $

(B) $ \lim_{x\to-\infty} k(x) = -\infty $ and $ \lim_{x\to\infty} k(x) = 0 $

(D) $ \lim_{x\to-\infty} k(x) = \infty $ and $ \lim_{x\to\infty} k(x) = 0 $

▶️ Answer/Explanation

Detailed solution

The correct option is (A).

Given the exponential function $ k(x) = -3(5)^x $, where $ a = -3 $ and $ b = 5 $.
Since the base $ b > 1 $, the term $ 5^x $ approaches $ \infty $ as $ x \to \infty $.
Multiplying by the negative coefficient $ a = -3 $, the limit becomes $ -\infty $. So, $ \lim_{x\to\infty} k(x) = -\infty $.
As $ x \to -\infty $, the term $ 5^x $ approaches $ 0 $ (since $ 5^{- \text{large}} = \frac{1}{5^{\text{large}}} $).
Therefore, $ -3 \cdot 0 = 0 $. So, $ \lim_{x\to-\infty} k(x) = 0 $.
This confirms that since $ b > 1 $ and $ a < 0 $, $ k(x) $ is an exponential growth function reflected over the $ x $-axis.

Question

The function $ j $ is given by $ j(x) = -5\left(\frac{1}{3}\right)^x $. Which of the following describes the end behavior of $ j $?

(A) $ \lim_{x\to-\infty} j(x) = 0 $ and $ \lim_{x\to\infty} j(x) = -\infty $

(B) $ \lim_{x\to-\infty} j(x) = -\infty $ and $ \lim_{x\to\infty} j(x) = 0 $

(D) $ \lim_{x\to-\infty} j(x) = \infty $ and $ \lim_{x\to\infty} j(x) = 0 $

▶️ Answer/Explanation

Detailed solution

The function is given by $ j(x) = a(b)^x $ with $ a = -5 $ and $ b = \frac{1}{3} $.
First, analyze the limit as $ x \to \infty $. Since the base $ 0 < \frac{1}{3} < 1 $, the term $ \left(\frac{1}{3}\right)^x $ approaches $ 0 $.
Multiplying by the coefficient $ -5 $, we get $ -5(0) = 0 $. Therefore, $ \lim_{x \to \infty} j(x) = 0 $.
Next, analyze the limit as $ x \to -\infty $. As $ x $ becomes a large negative number, $ \left(\frac{1}{3}\right)^x $ grows towards positive infinity (similar to $ 3^{|x|} $).
Multiplying this large positive value by the negative coefficient $ a = -5 $ results in a value approaching negative infinity.
Thus, $ \lim_{x \to -\infty} j(x) = -\infty $.
Geometrically, since $ 0 < b < 1 $ and $ a < 0 $, $ j(x) $ is an exponential decay function reflected over the $ x $-axis.
Comparing these findings with the given options, the correct description corresponds to option (B).

Question

The function $ f $ is given by $ f(x) = -\frac{1}{4}(3)^x $. Which of the following describes the end behavior of $ f $?

(A) $ \lim_{x\to-\infty} f(x) = 0 $ and $ \lim_{x\to\infty} f(x) = -\infty $

(B) $ \lim_{x\to-\infty} f(x) = -\infty $ and $ \lim_{x\to\infty} f(x) = 0 $

(D) $ \lim_{x\to-\infty} f(x) = \infty $ and $ \lim_{x\to\infty} f(x) = 0 $

▶️ Answer/Explanation

Detailed solution

The correct option is (A).

1. Identify the function parameters: base $ b = 3 $ and coefficient $ a = -\frac{1}{4} $.
2. Analyze the limit as $ x \to -\infty $: Since the base $ 3 > 1 $, the term $ 3^x $ approaches $ 0 $.
3. Therefore, $ \lim_{x \to -\infty} \left[ -\frac{1}{4}(3)^x \right] = -\frac{1}{4}(0) = 0 $.
4. Analyze the limit as $ x \to \infty $: The term $ 3^x $ grows towards $ \infty $ (exponential growth).
5. Multiplying by the negative coefficient $ a = -\frac{1}{4} $ drives the value towards negative infinity.
6. Therefore, $ \lim_{x \to \infty} \left[ -\frac{1}{4}(3)^x \right] = -\infty $.
7. Since $ b > 1 $ and $ a < 0 $, $ f(x) $ represents an exponential growth function reflected over the $ x $-axis.

Question

The function $ g $ is given by $ g(x)=-2\left(\frac{4}{3}\right)^x $. Which of the following describes the end behavior of $ g $?

(A) $ \lim_{x\to-\infty} g(x)=0 $ and $ \lim_{x\to\infty} g(x)=-\infty $

(B) $ \lim_{x\to-\infty} g(x)=-\infty $ and $ \lim_{x\to\infty} g(x)=0 $

(D) $ \lim_{x\to-\infty} g(x)=\infty $ and $ \lim_{x\to\infty} g(x)=0 $

▶️ Answer/Explanation

Detailed solution

The correct option is (A).

The function is in the form $ g(x) = a(b)^x $, with $ a = -2 $ and $ b = \frac{4}{3} $.
Since $ b > 1 $ and $ a < 0 $, $ g(x) $ is an exponential growth function reflected over the $ x $-axis.
As $ x \to \infty $: The base $ \frac{4}{3} > 1 $, so $ \left(\frac{4}{3}\right)^x \to \infty $. Multiplying by $ -2 $ makes the function approach $ -\infty $.
As $ x \to -\infty $:

Question

$x$	0	1	2	3	4
$f(x)$	36	18	9	$\frac{9}{2}$	$\frac{9}{4}$

The exponential function $f$ is defined by $f(x)=ab^x$, where $a$ and $b$ are positive constants. The table gives values of $f(x)$ at selected values of $x$. Which of the following statements is true?

(A) $f$ demonstrates exponential decay because $a > 0$ and $0 < b < 1$.

(B) $f$ demonstrates exponential decay because $a > 0$ and $b > 1$.

(D) $f$ demonstrates exponential growth because $a > 0$ and $b > 1$.

▶️ Answer/Explanation

Detailed solution

To determine the nature of the function, we find the values of constants $a$ and $b$.

Using the table value at $x=0$, we have $f(0) = a(b)^0 = a$. Since $f(0)=36$, then $a = 36$.

Using the table value at $x=1$, we have $f(1) = a(b)^1 = 36b$. Since $f(1)=18$, we solve $36b = 18$ to get $b = \frac{18}{36} = \frac{1}{2}$.

For an exponential function $f(x) = ab^x$ where $a > 0$, if the base $b$ satisfies $0 < b < 1$, the function represents exponential decay.

Here, $a = 36 > 0$ and $b = \frac{1}{2}$, which satisfies $0 < b < 1$.

Therefore, the statement in option (A) is correct.

Question

$ x $	$ 1 $	$ 2 $	$ 3 $	$ 4 $	$ 5 $
$ h(x) $	$ 2 $	$ 6 $	$ 18 $	$ 54 $	$ 162 $

The exponential function $ h $ is defined by $ h(x) = ab^x $, where $ a $ and $ b $ are positive constants. The table gives values of $ h(x) $ at selected values of $ x $. Which of the following statements is true?

(A) $ h $ demonstrates exponential decay because $ a > 0 $ and $ 0 < b < 1 $.

(B) $ h $ demonstrates exponential decay because $ a > 0 $ and $ b > 1 $.

(D) $ h $ demonstrates exponential growth because $ a > 0 $ and $ b > 1 $.

▶️ Answer/Explanation

Detailed solution

1. Observe the table values: as $ x $ increases by $ 1 $, $ h(x) $ increases ($ 2 \to 6 \to 18 \dots $), which indicates exponential growth.
2. Calculate the base $ b $ by taking the ratio of consecutive terms: $ b = \frac{h(2)}{h(1)} = \frac{6}{2} = 3 $.
3. Since $ b = 3 $, the condition $ b > 1 $ is satisfied.
4. To find $ a $, substitute the values from the first column ($ x=1, h(x)=2 $) into the equation $ h(x) = a \cdot b^x $.
5. This gives $ 2 = a \cdot 3^1 $, which simplifies to $ a = \frac{2}{3} $. This satisfies $ a > 0 $.
6. Therefore, the function demonstrates exponential growth because $ a > 0 $ and $ b > 1 $.
7. The correct choice is (D).

Question

$ x $	1	2	3	4	5
$ k(x) $	8	12	18	27	$ \frac{81}{2} $

The exponential function $ k $ is defined by $ k(x) = ab^x $, where $ a $ and $ b $ are positive constants. The table gives values of $ k(x) $ at selected values of $ x $. Which of the following statements is true?

(A) $ k $ demonstrates exponential decay because $ a > 0 $ and $ 0 < b < 1 $.

(B) $ k $ demonstrates exponential decay because $ a > 0 $ and $ b > 1 $.

(D) $ k $ demonstrates exponential growth because $ a > 0 $ and $ b > 1 $.

▶️ Answer/Explanation

Detailed solution

To identify the properties of the function, we first calculate the growth factor $ b $ by taking the ratio of consecutive $ k(x) $ values.

$ b = \frac{k(2)}{k(1)} = \frac{12}{8} = \frac{3}{2} $. Since $ \frac{3}{2} = 1.5 $, we have $ b > 1 $.

Next, we solve for the initial value $ a $ using the equation $ k(1) = ab^1 $.

$ 8 = a \left(\frac{3}{2}\right) \Rightarrow a = 8 \cdot \frac{2}{3} = \frac{16}{3} $. Thus, $ a $ is a positive constant ($ a > 0 $).

An exponential function represents growth when the base $ b > 1 $ and $ a > 0 $.

Therefore, $ k $ demonstrates exponential growth because $ a > 0 $ and $ b > 1 $.

Correct Option: (D)

Question

$ x $	0	1	2	3	4
$ f(x) $	54	36	24	16	$ \frac{32}{3} $

(A) $ f $ demonstrates exponential decay because $ a > 0 $ and $ 0 < b < 1 $.

(B) $ f $ demonstrates exponential decay because $ a > 0 $ and $ b > 1 $.

(D) $ f $ demonstrates exponential growth because $ a > 0 $ and $ b > 1 $.

▶️ Answer/Explanation

Detailed solution

To identify the correct statement, we first calculate the values of the constants $ a $ and $ b $.
Substitute $ x = 0 $ from the table into the function $ f(x) = ab^x $: $ f(0) = ab^0 = a(1) = a $.
From the table, $ f(0) = 54 $, therefore $ a = 54 $. This confirms that $ a > 0 $.
Next, substitute $ x = 1 $ into the function: $ f(1) = ab^1 = ab $.
From the table, $ f(1) = 36 $. So, $ 54b = 36 $.
Solving for $ b $, we get $ b = \frac{36}{54} = \frac{2}{3} $.
Since $ b = \frac{2}{3} $, the base falls in the range $ 0 0 $ and $ 0 < b < 1 $ represents exponential decay.
Thus, statement (A) is the correct description.

Question

Which of the following statements is true about the exponential function $ f $ given by $ f(x)=4\left(\frac{1}{3}\right)^x $?

(A) $ f $ is always increasing, and the graph of $ f $ is always concave up.

(B) $ f $ is always increasing, and the graph of $ f $ is always concave down.

(D) $ f $ is always decreasing, and the graph of $ f $ is always concave down.

▶️ Answer/Explanation

Detailed solution

The given function is $ f(x) = 4\left(\frac{1}{3}\right)^x $, which is in the form $ f(x) = a \cdot b^x $.
Here, $ a = 4 $ (which is $ > 0 $) and the base $ b = \frac{1}{3} $.
Since $ a > 0 $ and $ 0 0 $) curves upward like a cup, meaning it is concave up.
Mathematically, the second derivative $ f”(x) = 4(\ln(1/3))^2(1/3)^x $ is always positive, confirming concavity is up.
Therefore, $ f $ is always decreasing, and the graph of $ f $ is always concave up.
Correct Option: (C)

Question

Which of the following statements is true about the exponential function $ g $ given by $ g(x) = \frac{1}{2} \cdot 3^x $?

(A) $ g $ is always increasing, and the graph of $ g $ is always concave up.

(B) $ g $ is always increasing, and the graph of $ g $ is always concave down.

(D) $ g $ is always decreasing, and the graph of $ g $ is always concave down.

▶️ Answer/Explanation

Detailed solution

The function is defined as $ g(x) = \frac{1}{2} \cdot 3^x $, which fits the form $ f(x) = a \cdot b^x $.
Here, the initial value $ a = \frac{1}{2} $ is positive ($ a > 0 $) and the base $ b = 3 $ is greater than 1 ($ b > 1 $).
Since $ a > 0 $ and $ b > 1 $, the function represents exponential growth, meaning $ g $ is always increasing.
As $ x $ increases, the slope of the graph becomes steeper, which indicates the graph curves upward.
Mathematically, the second derivative $ g”(x) = \frac{1}{2} (\ln 3)^2 \cdot 3^x $ is always positive.
A positive second derivative confirms that the graph is always concave up.
Therefore, statement (A) is the correct description of the function.

Question

Which of the following statements is true about the exponential function $ h $ given by $ h(x)=3 \cdot 5^x $?

(A) $ h $ is always increasing, and the graph of $ h $ is always concave up.

(B) $ h $ is always increasing, and the graph of $ h $ is always concave down.

(D) $ h $ is always decreasing, and the graph of $ h $ is always concave down.

▶️ Answer/Explanation

Detailed solution

The correct option is (A).

1. The function is given by $ h(x) = 3 \cdot 5^x $, which is in the form $ f(x) = a \cdot b^x $.

2. Identify the constants: $ a = 3 $ and $ b = 5 $.

3. Since $ a > 0 $ and $ b > 1 $, the function represents exponential growth.

4. An exponential growth function is always increasing because the base (5) is greater than 1.

5. The graph of an exponential growth function curves upward like a “cup”, which means it is concave up.

6. Mathematically, the second derivative $ h”(x) = 3 \cdot (\ln 5)^2 \cdot 5^x $ is always positive, confirming the graph is concave up.

7. Therefore, $ h $ is always increasing and its graph is always concave up.

Question

Which of the following statements is true about the exponential function $k$ given by $k(x) = -4 \cdot 3^x$?

(A) $k$ is always increasing, and the graph of $k$ is always concave up.

(B) $k$ is always increasing, and the graph of $k$ is always concave down.

(D) $k$ is always decreasing, and the graph of $k$ is always concave down.

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

1. The function is given by $k(x) = -4 \cdot 3^x$, which is in the form $f(x) = a \cdot b^x$.
2. Here, the base $b = 3$. Since $b > 1$, the parent function $3^x$ represents exponential growth (increasing and concave up).
3. The leading coefficient is $a = -4$. Since $a < 0$, the graph is reflected over the $x$-axis.
4. When an increasing function is reflected over the $x$-axis, it becomes a decreasing function.
5. When a concave up graph is reflected over the $x$-axis, the concavity changes to concave down.
6. Therefore, $k$ is always decreasing, and the graph of $k$ is always concave down.

Question

Which of the following statements is true about the exponential function $ j $ given by $ j(x)=-6\left(\frac{2}{7}\right)^x $?

(A) $ j $ is always increasing, and the graph of $ j $ is always concave up.

(B) $ j $ is always increasing, and the graph of $ j $ is always concave down.

(D) $ j $ is always decreasing, and the graph of $ j $ is always concave down.

▶️ Answer/Explanation

Detailed solution

The exponential function is in the form $ j(x) = a \cdot b^x $, with $ a = -6 $ and base $ b = \frac{2}{7} $.
First, analyze the base: since $ 0 < \frac{2}{7} < 1 $, the term $ \left(\frac{2}{7}\right)^x $ represents exponential decay and is naturally decreasing.
Next, analyze the coefficient: $ a = -6 $ is negative, which reflects the graph over the x-axis.
Reflecting a decreasing function over the x-axis reverses its direction, making $ j(x) $ always increasing.
Regarding concavity, the basic decay function $ b^x $ is always concave up (curves upward).
Reflecting a concave up graph over the x-axis inverts its curvature, making it concave down.
Mathematically, the second derivative is $ j”(x) = -6 \left(\ln \frac{2}{7}\right)^2 \left(\frac{2}{7}\right)^x $, which is always negative.
Therefore, the function is always increasing and the graph is always concave down.

Question

Which of the following statements is true about the exponential function $ f $ given by $ f(x) = -\frac{1}{3} \cdot 2^x $?

(A) $ f $ is always increasing, and the graph of $ f $ is always concave up.

(B) $ f $ is always increasing, and the graph of $ f $ is always concave down.

(D) $ f $ is always decreasing, and the graph of $ f $ is always concave down.

▶️ Answer/Explanation

Detailed solution

The correct option is (D).

1. The function is given by $ f(x) = a \cdot b^x $, where $ a = -\frac{1}{3} $ and $ b = 2 $.
2. Since the base $ b = 2 $ is greater than $ 1 $, the parent function $ y = 2^x $ represents exponential growth, which is increasing and concave up.
3. The coefficient $ a = -\frac{1}{3} $ is negative ($ a < 0 $).
4. As stated in the problem’s note: if $ a < 0 $ and $ b > 1 $, then $ f(x) $ is an exponential growth function reflected over the $ x $-axis.
5. Reflecting an increasing function over the $ x $-axis results in a function that is always decreasing.
6. Reflecting a graph that is concave up over the $ x $-axis results in a graph that is always concave down.
7. Therefore, $ f $ is always decreasing, and the graph of $ f $ is always concave down.

Question

Which of the following statements is true about the exponential function $ f $ given by $ f(x) = 7 \left( \frac{4}{5} \right)^x $?

(A) $ f $ is increasing at an increasing rate.

(B) $ f $ is increasing at a decreasing rate.

(D) $ f $ is decreasing at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

The correct answer is (C).

The function is given by $ f(x) = 7(0.8)^x $. Since the base $ 0.8 < 1 $, the function represents exponential decay, meaning $ f(x) $ is decreasing.
The rate of change is given by the derivative $ f'(x) $. Since $ f'(x) $ is negative but approaching zero (becoming less negative) as $ x $ increases, the value of the rate is mathematically increasing.
Geometrically, the graph is concave up ( $ f”(x) > 0 $ ), which indicates that the slope of the tangent line is increasing.
Therefore, $ f $ is decreasing at an increasing rate.

Question

Which of the following statements is true about the exponential function $g$ given by $g(x) = -6 \cdot 5^x$ ?

(A) $g$ is increasing at an increasing rate.

(B) $g$ is increasing at a decreasing rate.

(D) $g$ is decreasing at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

The function is defined as $g(x) = -6 \cdot 5^x$, which is an exponential function of the form $ab^x$.
Here, the base $b = 5 > 1$ suggests growth, but the coefficient $a = -6 < 0$ causes a reflection over the $x$-axis.
Because of this reflection, as $x$ increases, the value of $g(x)$ moves further away from $0$ in the negative direction, meaning $g$ is decreasing.
To determine the rate, we look at concavity: since $a < 0$, the graph is concave down.
Being concave down indicates that the slope (rate of change) is becoming more negative as $x$ increases.
Thus, the rate of change is decreasing.
Therefore, $g$ is decreasing at a decreasing rate.

Correct Option: (D)

Question

Which of the following statements is true about the exponential function $h$ given by $h(x)=4 \cdot 9^x$ ?

(A) $h$ is increasing at an increasing rate.

(B) $h$ is increasing at a decreasing rate.

(D) $h$ is decreasing at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

Correct Answer: (A)

For the exponential function $h(x) = a \cdot b^x$, we identify the parameters $a = 4$ and $b = 9$.
Since the coefficient $a > 0$ and the base $b > 1$, $h(x)$ is an exponential growth function.
This implies that as $x$ increases, the value of $h(x)$ is strictly increasing.
Furthermore, the graph of an exponential growth function is concave up.
Concavity indicates that the slope of the tangent line gets steeper as $x$ increases.
Therefore, $h$ is increasing at an increasing rate.

Question

The figure shows a portion of the graph of a function $ h $. Which of the following conclusions is possible for $ h $?

(A) $ h $ is logarithmic because the output values are proportional over equal-length input-value intervals.

(B) $ h $ is logarithmic because the input values are proportional over equal-length output-value intervals.

(D) $ h $ is exponential because the input values are proportional over equal-length output-value intervals.

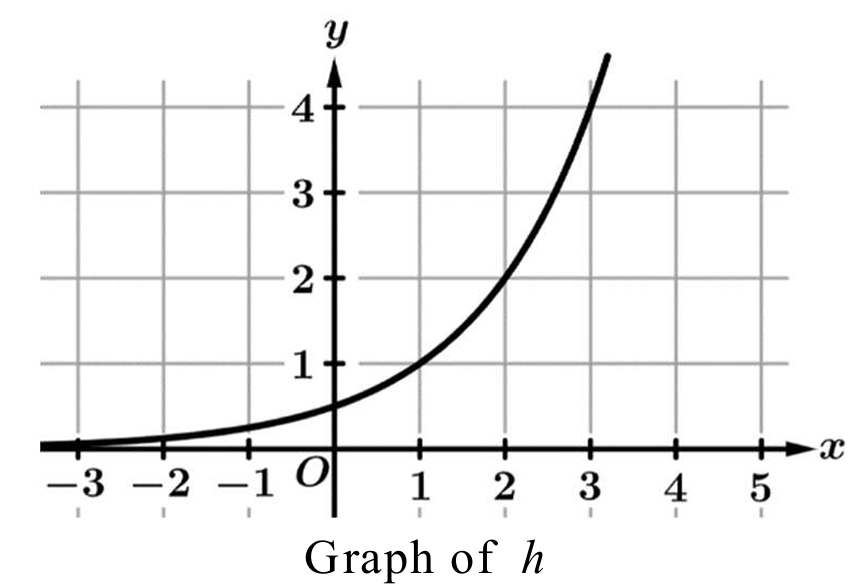
▶️ Answer/Explanation

Detailed solution

1. Examine the coordinates of points on the graph: specifically, the points $(1, 1)$, $(2, 2)$, and $(3, 4)$ are clearly identifiable.

2. Analyze the input intervals: The step from $x = 1$ to $x = 2$ is an increase of $1$, and from $x = 2$ to $x = 3$ is also an increase of $1$. These are equal-length input-value intervals.

3. Analyze the corresponding output values: As $x$ increases by $1$, $y$ changes from $1$ to $2$, and then from $2$ to $4$.

4. Calculate the ratio of outputs: $\frac{2}{1} = 2$ and $\frac{4}{2} = 2$. The output values are being multiplied by a constant factor of $2$.

5. This behavior, where output values change by a constant ratio (are proportional) over equal arithmetic steps in the input, defines an exponential function.

6. A logarithmic function would exhibit the inverse relationship (inputs proportional over equal output intervals).

7. Therefore, the correct conclusion is that $ h $ is exponential because the output values are proportional over equal-length input-value intervals.

Correct Option: (C)

Question

The figure shows a portion of the graph of a function $ g $. Which of the following conclusions is possible for $ g $?

(A) $ g $ is logarithmic because the output values are proportional over equal-length input-value intervals.

(B) $ g $ is logarithmic because the input values are proportional over equal-length output-value intervals.

(D) $ g $ is exponential because the input values are proportional over equal-length output-value intervals.

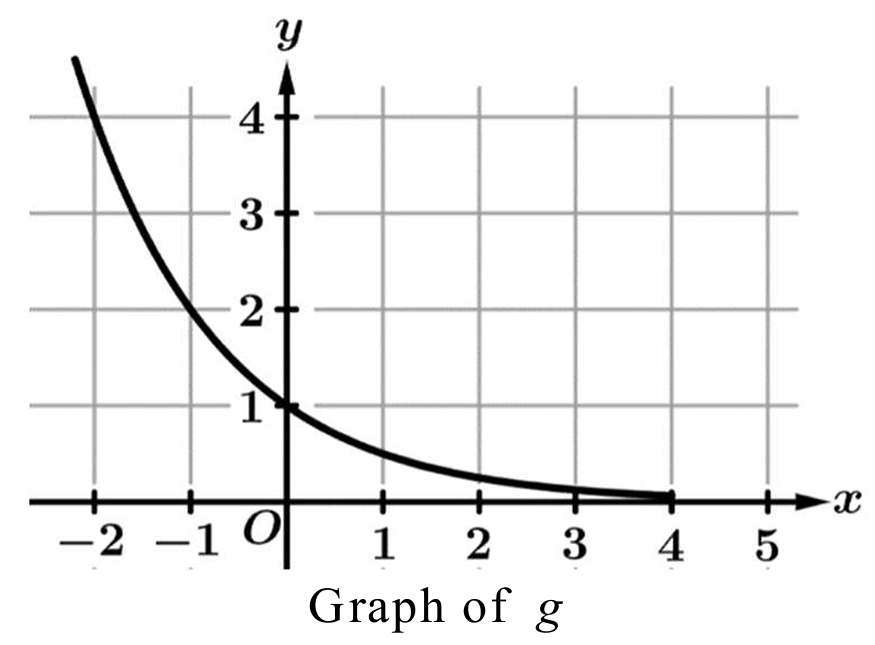
▶️ Answer/Explanation

Detailed solution

The correct option is (C).

1. Examine the points on the graph: $ (-2, 4) $, $ (-1, 2) $, and $ (0, 1) $.
2. Analyze the change in output values ($ y $) as the input values ($ x $) increase by a constant interval of $ 1 $.
3. From $ x = -2 $ to $ x = -1 $, the output changes from $ 4 $ to $ 2 $, which is a factor of $ \frac{1}{2} $.
4. From $ x = -1 $ to $ x = 0 $, the output changes from $ 2 $ to $ 1 $, which is again a factor of $ \frac{1}{2} $.
5. A function where output values are multiplied by a constant factor over equal-length input intervals is an exponential function.
6. Specifically, as noted in the image, the output values are multiplied by $ \frac{1}{2} $ over equal-length input-value intervals.
7. Therefore, $ g $ is exponential because the output values are proportional over equal-length input-value intervals.

Question

The figure shows a portion of the graph of a function $f$. Which of the following conclusions is possible for $f$?

(A) $f$ is quadratic because the output values are proportional over equal-length input-value intervals.

(B) $f$ is quadratic because the average rates of change over consecutive equal-length input-value intervals can be given by a linear function.

(D) $f$ is exponential because the average rates of change over consecutive equal-length input-value intervals can be given by a linear function.

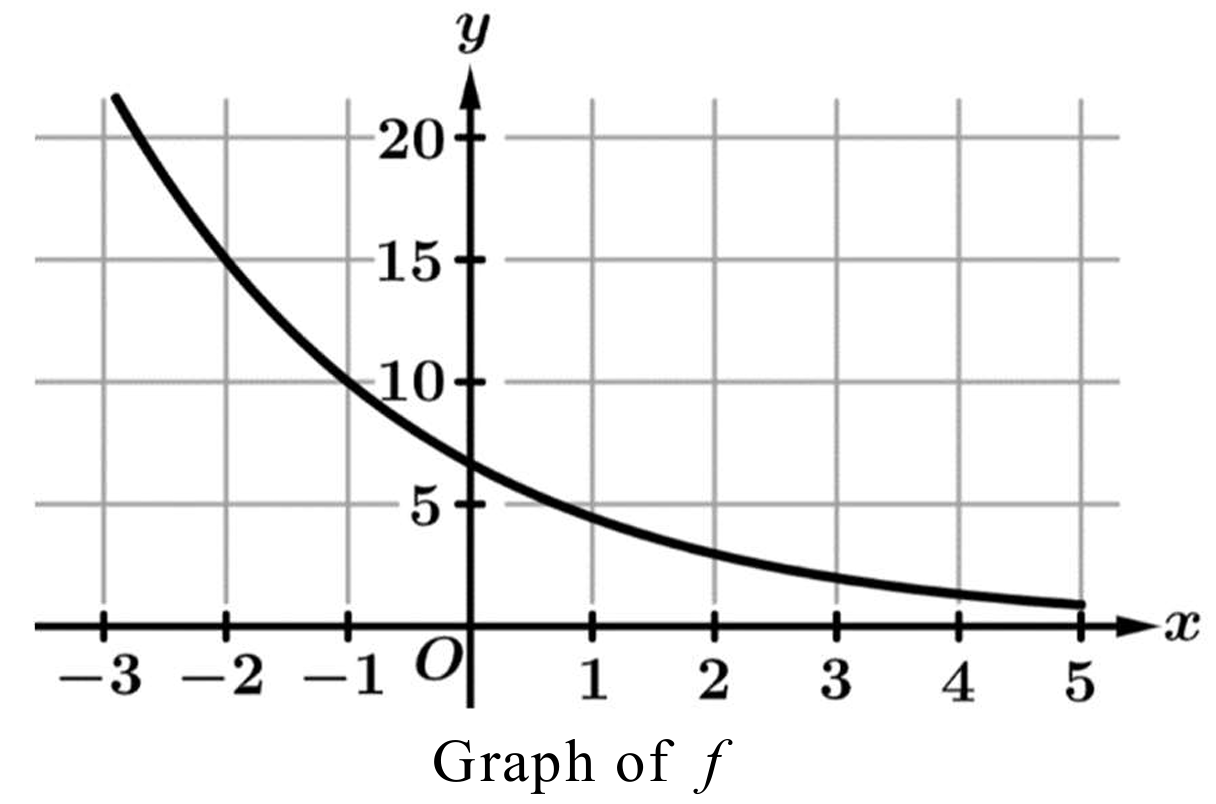
▶️ Answer/Explanation

Detailed solution

The correct option is (C).
By observing the graph, at $x = -2$, $y \approx 15$, and at $x = -1$, $y = 10$.
The output values are multiplied by a constant ratio of $\frac{10}{15} = \frac{2}{3}$ over equal intervals of $\Delta x = 1$.
This constant proportionality of output values is the defining characteristic of an exponential function.
Option (B) describes a property of quadratic functions, but the graph shows asymptotic behavior toward the $x$-axis.
Option (D) is incorrect because exponential rates of change are themselves exponential, not linear.
Therefore, $f$ is exponential because the outputs are proportional over equal-length input intervals.

Question

At time $t = 0$ years, the population of a certain city was $23,144$. During each of the next $10$ years, the population decreased by $4\%$ per year. Based on this information, which of the following models the population as a function of $t$, in years, for $0 \le t \le 10$?

(A) $23,144 – 0.04t$

(B) $23,144 – 0.96t$

(D) $23,144(1.04)^t$

▶️ Answer/Explanation

Detailed solution

The problem describes a population changing by a fixed percentage each year, which requires an exponential model.
The general formula for exponential decay is $y = a(1 – r)^t$, where $a$ is the initial amount and $r$ is the rate.
The initial population is given as $23,144$.
The population decreases by $4\%$ per year, so the rate $r = 0.04$.
The decay factor is calculated as $1 – 0.04 = 0.96$.
Substituting these values into the formula gives $23,144(0.96)^t$.
This corresponds to option (C).

Question

The exponential function $f$ is defined by $f(x) = ab^x$, where $a$ and $b$ are positive constants. The table gives values of $f(x)$ at selected values of $x$. Which of the following statements is true?

(A) $f$ demonstrates exponential decay because $a > 0$ and $0 < b < 1$.

(B) $f$ demonstrates exponential decay because $a > 0$ and $b > 1$.

(D) $f$ demonstrates exponential growth because $a > 0$ and $b > 1$.

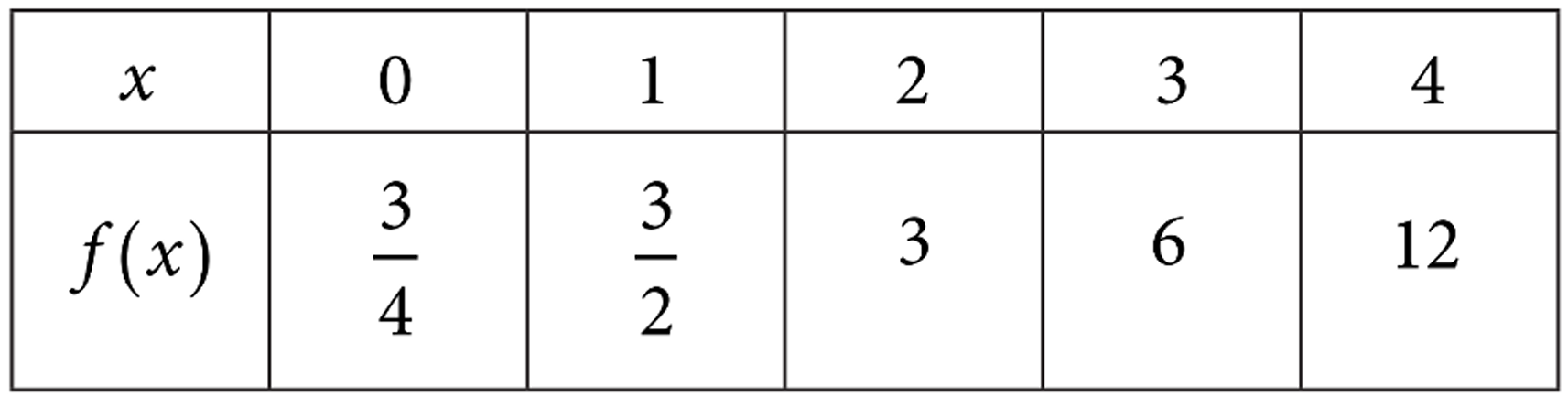
▶️ Answer/Explanation

Detailed solution

To determine the behavior of the function, we must find the values of $a$ and $b$.
First, substitute $x = 0$ into $f(x) = ab^x$. Since $f(0) = \frac{3}{4}$, we have $a(b)^0 = a = \frac{3}{4}$. Thus, $a > 0$.
Next, substitute $x = 1$ to find $b$. Since $f(1) = \frac{3}{2}$, we have $f(1) = a(b)^1 \Rightarrow \frac{3}{4}(b) = \frac{3}{2}$.
Solving for $b$, we multiply both sides by $\frac{4}{3}$: $b = \frac{3}{2} \cdot \frac{4}{3} = 2$.
An exponential function exhibits growth when the base $b > 1$ and decay when $0 0$).
Since we calculated that $b = 2$, which is greater than $1$, the function demonstrates exponential growth.
Therefore, statement (D) is the correct description.

Correct Option: (D)

Question

The function $h$ is given by $h(x) = 8 \cdot 2^{x}$. For which of the following values of $x$ is $h(x) = 256$?

(A) $x = 2$
(B) $x = 5$
(C) $x = 8$
(D) $x = 16$

▶️ Answer/Explanation

Detailed solution

Set the function equal to the target value: $8 \cdot 2^{x} = 256$.
Divide both sides by $8$ to isolate the exponential term: $2^{x} = \frac{256}{8}$.
Simplify the division: $2^{x} = 32$.
Express $32$ as a power of $2$, which is $2^{5}$.
Since the bases are the same, equate the exponents: $x = 5$.
Therefore, the correct option is (B).

Question

The figure below shows a portion of the graph of a function $f$ that has the $x$-axis as a horizontal asymptote. The function $f$ exhibits exponential decay. Which of the following describes $f$?

(A) $\lim_{x \to \infty} f(x) = -\infty$

(B) $\lim_{x \to \infty} f(x) = \infty$

(D) $\lim_{x \to -\infty} f(x) = \infty$

▶️ Answer/Explanation

Detailed solution

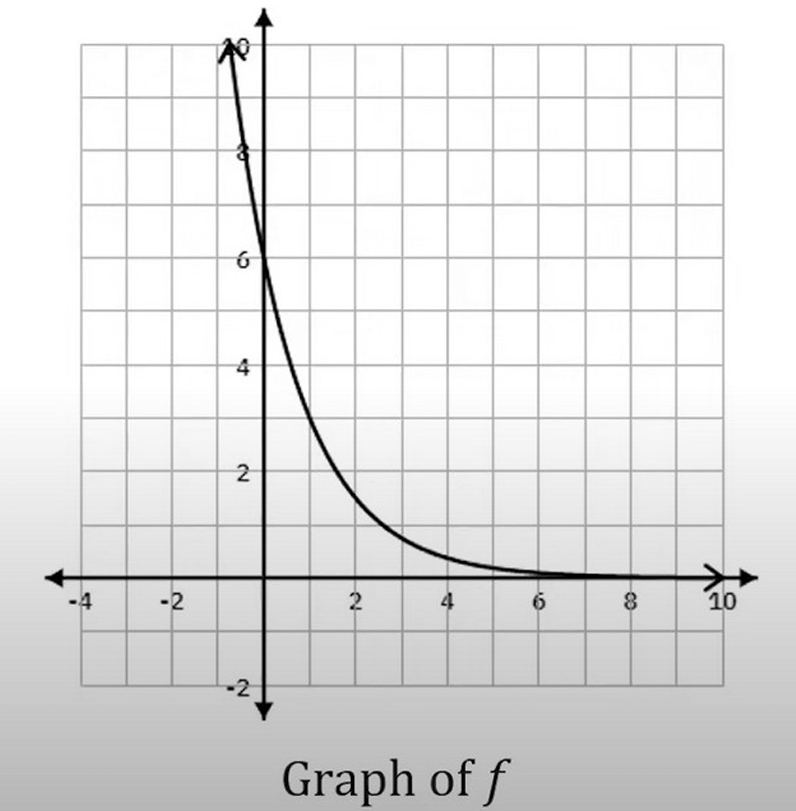
The function $f$ is described as an exponential decay function with the $x$-axis as a horizontal asymptote.
Looking at the graph, as $x$ moves to the right ($x \to \infty$), the curve approaches the x-axis, implying $\lim_{x \to \infty} f(x) = 0$.
Looking at the left side of the graph, as $x$ moves to the left ($x \to -\infty$), the curve goes up steeply.
This upward trend indicates that the function values increase without bound as $x$ decreases.
Mathematically, this behavior is written as $\lim_{x \to -\infty} f(x) = \infty$.
Comparing this result with the given choices, option (D) is the correct description.

Question

The function $f$ is given by $f(x) = a \cdot c^x$, where $a > 0$ and $c > 1$. Which of the following is true about the values of constants $m$ and $b$ in the equation $\ln(f(x)) = mx + b$?

(A) $m > 0$ because $\ln c > 0$; $b$ can be any real number because $\ln a$ can be any real number.
(B) $m > 0$ because $\ln c > 0$; $b > 0$ because $\ln a > 0$.
(C) $m$ can be any real number because $\ln c$ can be any real number; $b$ can be any real number because $\ln a$ can be any real number.
(D) $m$ can be any real number because $\ln c$ can be any real number; $b > 0$ because $\ln a > 0$.

▶️ Answer/Explanation

Detailed solution

Take the natural log of the function: $\ln(f(x)) = \ln(a \cdot c^x)$.
Apply log properties: $\ln(f(x)) = \ln a + \ln(c^x) = (\ln c)x + \ln a$.
Comparing this to $mx + b$, we find $m = \ln c$ and $b = \ln a$.
Since $c > 1$, it follows that $\ln c > 0$, so $m > 0$.
Since $a > 0$, the value of $b = \ln a$ can be any real number ($-\infty < \ln a < \infty$).
Therefore, $m > 0$ and $b$ can be any real number.
The correct option is (A).

Question

The function $ j $ is given by $ j(x) = -5\left(\frac{1}{3}\right)^x $. Which of the following describes the end behavior of $ j $?

(A) $ \lim_{x \to -\infty} j(x) = 0 $ and $ \lim_{x \to \infty} j(x) = -\infty $

(B) $ \lim_{x \to -\infty} j(x) = -\infty $ and $ \lim_{x \to \infty} j(x) = 0 $

(D) $ \lim_{x \to -\infty} j(x) = \infty $ and $ \lim_{x \to \infty} j(x) = 0 $

▶️ Answer/Explanation

Detailed solution

The given function is an exponential function defined as $ j(x) = -5\left(\frac{1}{3}\right)^x $.
First, analyze the limit as $ x \to \infty $. Since the base $ \frac{1}{3} $ is between $ 0 $ and $ 1 $, $ \left(\frac{1}{3}\right)^x $ approaches $ 0 $ as $ x $ gets larger.
Therefore, $ j(x) $ approaches $ -5 \cdot 0 = 0 $, so $ \lim_{x \to \infty} j(x) = 0 $.
Next, analyze the limit as $ x \to -\infty $. A negative exponent flips the fraction, so $ \left(\frac{1}{3}\right)^{-\infty} $ acts like $ 3^{\infty} $, which approaches $ \infty $.
Multiplying this large positive value by $ -5 $ results in a large negative value, so $ \lim_{x \to -\infty} j(x) = -\infty $.
Comparing these results with the given options, the correct description corresponds to option (B).

Question

The exponential function $f$ is defined by $f(x) = ab^{x}$, where $a$ and $b$ are positive constants. The table gives values of $f(x)$ at selected values of $x$. Which of the following statements is true?

(A) $f$ demonstrates exponential decay because $a > 0$ and $0 < b < 1$.

(B) $f$ demonstrates exponential decay because $a > 0$ and $b > 1$.

(D) $f$ demonstrates exponential growth because $a > 0$ and $b > 1$.

▶️ Answer/Explanation

Detailed solution

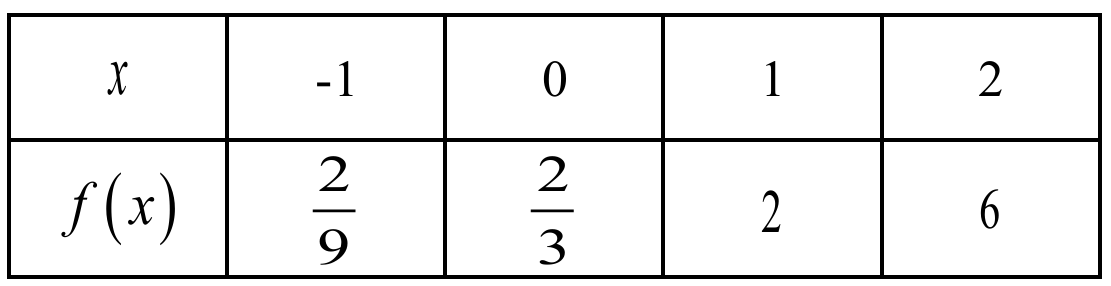
The correct option is (D).
Identify the $y$-intercept from the table: at $x = 0$, $f(0) = \frac{2}{3}$, so $a = \frac{2}{3}$, which is $> 0$.
Determine the common ratio $b$ by calculating $\frac{f(x+1)}{f(x)}$, for example: $\frac{f(1)}{f(0)} = \frac{2}{2/3} = 3$.
Since $b = 3$, it follows that $b > 1$.
An exponential function $f(x) = ab^{x}$ with $a > 0$ and $b > 1$ represents exponential growth.
As $x$ increases, the values of $f(x)$ in the table ($\frac{2}{9}, \frac{2}{3}, 2, 6$) are strictly increasing.
Therefore, $f$ demonstrates exponential growth because $a > 0$ and $b > 1$.

Question

The function $g$ is given by $g(x) = -2 \left( \frac{1}{5} \right)^x$. Which of the following limit statements is true about the graph of $g(x)$?

(A) $\lim_{x \to -\infty} g(x) = 0$ and $\lim_{x \to \infty} g(x) = \infty$

(B) $\lim_{x \to -\infty} g(x) = 0$ and $\lim_{x \to \infty} g(x) = -\infty$

(D) $\lim_{x \to -\infty} g(x) = -\infty$ and $\lim_{x \to \infty} g(x) = 0$

▶️ Answer/Explanation

Detailed solution

The correct option is (D).
As $x \to \infty$, the term $\left( \frac{1}{5} \right)^x$ approaches $0$, so $g(x) = -2(0) = 0$.
As $x \to -\infty$, the term $\left( \frac{1}{5} \right)^x$ is equivalent to $5^{-x}$, which becomes $5^{\infty} = \infty$.
Multiplying this positive infinity by the constant $-2$ results in $-\infty$.
Therefore, $\lim_{x \to -\infty} g(x) = -\infty$ and $\lim_{x \to \infty} g(x) = 0$.
This matches the behavior of a reflected exponential decay function.
The horizontal asymptote is the line $y = 0$.

Question

A dog food bowl has a certain number of dog food pellets in the bowl. A dog eats the bowl fast at first but slows down over time. This perfectly correlates to a fraction of the remaining dog food being eaten per minute. To predict how long it will take for the dog to finish his food, he times the dog and finds that (1) minute after starting to eat, the dog bowl has (145) pellets left. After (2) minutes, there are (115) pellets in the bowl. This situation can be modeled by an exponential function, where $P(t) = ae^{bt}$, $P(t)$ is the number of pellets in the bowl, and $t$ is the time in minutes after the dog has started eating.

(A) Find an exponential function that models this situation.

(B) i. Find the average rate of change from $t = 0$ to $t = 4$. Explain its meaning in context of the problem.

ii. Will the rate of change from $t = 4$ to $t = t_a$, where $t_a > 4$, be greater or less than the rate of change from $t = 0$ to $t = 4$? Justify your answer using your knowledge of the exponential function and its concavity.

(C) When $t$ increases to infinity without bound, does this model still make sense in context of the problem? Why or why not?

Most-appropriate topic codes (CED):

• TOPIC 2.5: Exponential Function Context and Data Modeling — parts (A), (B)i, (C)
• TOPIC 2.2: Change in Linear and Exponential Functions — part (B)ii

▶️ Answer/Explanation

(A) Find the exponential function
We are given the model $P(t) = ae^{bt}$ and two points: $(1, 145)$ and $(2, 115)$.

Step 1: Set up the equations.
$$145 = ae^{b(1)} \quad \text{(Eq. 1)}$$
$$115 = ae^{b(2)} \quad \text{(Eq. 2)}$$
Step 2: Divide Eq. 2 by Eq. 1 to solve for $e^b$.
$$\frac{115}{145} = \frac{ae^{2b}}{ae^b} \implies \frac{23}{29} = e^b$$
$$b = \ln\left(\frac{23}{29}\right) \approx -0.2318$$
Step 3: Substitute back to find $a$.
$$a = \frac{145}{e^b} = \frac{145}{23/29} = 145 \cdot \frac{29}{23} \approx 182.83$$

Function: $P(t) = 182.83 e^{-0.2318t}$

(B) i. Average Rate of Change
Calculate $P(0)$ and $P(4)$:

$P(0) = a \approx 182.83$
$P(4) = 182.83 \cdot e^{-0.2318(4)} \approx 72.35$

$$AROC = \frac{P(4) – P(0)}{4 – 0} = \frac{72.35 – 182.83}{4} \approx -27.62$$
Meaning: On average, the number of pellets in the bowl decreases by approximately 27.62 pellets per minute during the first 4 minutes.

(B) ii. Comparison of Rates
The rate of change from $t=4$ to $t=t_a$ will be greater (less negative) than the rate from $t=0$ to $t=4$.
Justification: The function $P(t)$ represents exponential decay. The second derivative $P”(t) = ab^2e^{bt}$ is positive (since $a>0$ and $b^2>0$), which means the graph is concave up. For a concave up function, the rate of change (slope) increases as $t$ increases. Thus, the slope becomes less negative (closer to zero) over time.

(C) Model Validity at Infinity
No, the model does not make sense as $t \to \infty$.
While the mathematical limit $\lim_{t \to \infty} P(t) = 0$, the function never actually reaches zero; it only approaches it asymptotically. In reality, the dog will finish the food (reach exactly 0 pellets) in a finite amount of time. Additionally, pellets are discrete units, whereas the model predicts fractional amounts of pellets.

\(x\)	0	1	2	3	4
\(f(x)\)	36	18	9	\(\frac{9}{2}\)	\(\frac{9}{4}\)

\( x \)	\( 1 \)	\( 2 \)	\( 3 \)	\( 4 \)	\( 5 \)
\( h(x) \)	\( 2 \)	\( 6 \)	\( 18 \)	\( 54 \)	\( 162 \)