AP Precalculus -2.3 Exponential Functions- Study Notes - Effective Fall 2023
AP Precalculus -2.3 Exponential Functions- Study Notes – Effective Fall 2023
AP Precalculus -2.3 Exponential Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify key characteristics of exponential functions.
Key Concepts:
Exponential Functions, Growth, and Decay
Exponential Functions and the Meaning of the Input
Monotonicity, Concavity, and Extrema of Exponential Functions
Using Additive Transformations to Identify Exponential Functions
End Behavior of Exponential Functions
Exponential Functions, Growth, and Decay
An exponential function is a function in which the input variable appears in the exponent.
The general form of an exponential function is
\( \mathrm{ \displaystyle f(x) = ab^x } \)
where:
• \( \mathrm{a} \) is the initial value, with \( \mathrm{a \ne 0} \)
• \( \mathrm{b} \) is the base, with \( \mathrm{b > 0} \) and \( \mathrm{b \ne 1} \)
The value of \( \mathrm{b} \) determines whether the function represents growth or decay.
Exponential Growth
When \( \mathrm{a > 0} \) and \( \mathrm{b > 1} \), the function demonstrates exponential growth.
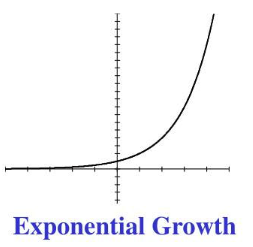
In this case, the output values increase at an increasing rate as the input increases.
Exponential Decay
When \( \mathrm{a > 0} \) and \( \mathrm{0 < b < 1} \), the function demonstrates exponential decay.
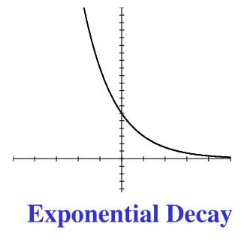
In this case, the output values decrease and approach zero as the input increases.
Exponential functions model situations involving population growth, compound interest, radioactive decay, and cooling processes.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = 5 \cdot 2^x } \)
Determine whether the function represents exponential growth or decay.
▶️ Answer/Explanation
Here, \( \mathrm{a = 5 > 0} \) and \( \mathrm{b = 2 > 1} \).
The base is greater than 1, so the function increases as \( \mathrm{x} \) increases.
Conclusion
The function demonstrates exponential growth.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = 120(0.75)^x } \)
Determine whether the function represents exponential growth or decay.
▶️ Answer/Explanation
Here, \( \mathrm{a = 120 > 0} \) and \( \mathrm{0 < b = 0.75 < 1} \).
The base is between 0 and 1, so the output values decrease as \( \mathrm{x} \) increases.
Conclusion
The function demonstrates exponential decay.
Exponential Functions and the Meaning of the Input
An exponential function has the general form
\( \mathrm{ \displaystyle f(x) = ab^x } \)
When the input values are natural numbers, the input \( \mathrm{x} \) specifies the number of factors of the base applied to the initial value.
For example:
• \( \mathrm{f(1) = ab} \) means the initial value is multiplied by the base once
• \( \mathrm{f(2) = ab^2} \) means the initial value is multiplied by the base twice
• \( \mathrm{f(3) = ab^3} \) means the initial value is multiplied by the base three times
Thus, natural-number inputs represent repeated multiplication by the base.
Although this repeated-multiplication interpretation comes from natural-number inputs, the domain of an exponential function is all real numbers.
This allows exponential functions to model continuous growth and decay, not just step-by-step change.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = 5 \cdot 3^x } \)
Evaluate the function for natural-number inputs.
▶️ Answer/Explanation
Compute the values:
\( \mathrm{ f(1) = 5 \cdot 3 = 15 } \)
\( \mathrm{ f(2) = 5 \cdot 3^2 = 45 } \)
\( \mathrm{ f(3) = 5 \cdot 3^3 = 135 } \)
Conclusion
Each increase of 1 in the input adds one more factor of 3.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = 10 \cdot 2^x } \)
Explain the meaning of the domain.
▶️ Answer/Explanation
When \( \mathrm{x} \) is a natural number, the function represents repeated multiplication by 2.
When \( \mathrm{x} \) is any real number, the function still produces a valid output.
Therefore, the domain is
\( \mathrm{ (-\infty, \infty) } \)
Conclusion
Exponential functions are defined for all real inputs, allowing continuous modeling.
Monotonicity, Concavity, and Extrema of Exponential Functions
An exponential function in general form
\( \mathrm{ \displaystyle f(x) = ab^x } \)
has the property that its output values change proportionally over equal-length input-value intervals.
Mathematically, for a fixed interval length \( \mathrm{h} \),
\( \mathrm{ \displaystyle \dfrac{f(x+h)}{f(x)} = b^h } \)
which is constant for all values of \( \mathrm{x} \).
Because of this proportional change:
• If \( \mathrm{b > 1} \), the function is always increasing
• If \( \mathrm{0 < b < 1} \), the function is always decreasing
Thus, exponential functions are monotonic on their entire domains.
In addition, the rate of change of an exponential function is itself changing in a consistent way. As a result, the graph of an exponential function is always concave up or always concave down, depending on the sign of \( \mathrm{a} \).
Because the concavity never changes, exponential functions:
• Do not have points of inflection
• Do not have local maxima or minima on their entire domain
An exponential function may have an extreme value only on a closed interval, where the maximum or minimum occurs at an endpoint.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = 2^x } \)
Describe its increasing or decreasing behavior and concavity.
▶️ Answer/Explanation
Here, the base is \( \mathrm{b = 2 > 1} \).
Therefore, the function is always increasing.
The rate of change increases as \( \mathrm{x} \) increases, so the graph is concave up everywhere.
Conclusion
The function has no local maximum, no local minimum, and no point of inflection.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = 5(0.6)^x } \)
Explain why this function has no extrema on its entire domain.
▶️ Answer/Explanation
The base satisfies \( \mathrm{0 < b = 0.6 < 1} \).
Therefore, the function is always decreasing.
Since the function never changes direction and its concavity does not change, it has no local maximum or minimum.
Any extreme value can only occur at an endpoint of a closed interval.
Conclusion
The function has no extrema on its entire domain and no point of inflection.
Using Additive Transformations to Identify Exponential Functions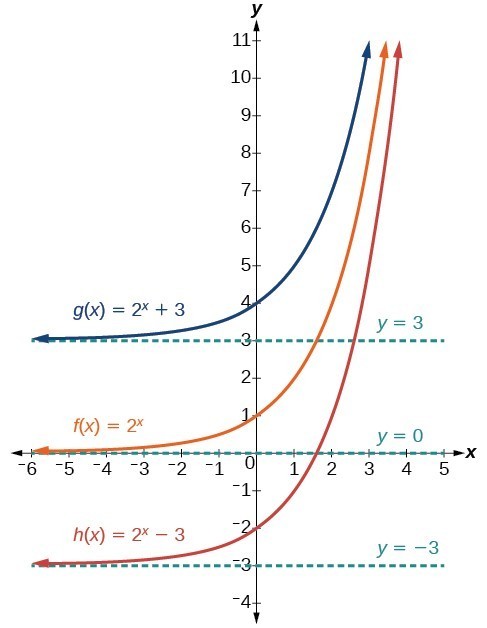
Let \( \mathrm{f} \) be a function, and let
\( \mathrm{ \displaystyle g(x) = f(x) + k } \)
be an additive transformation of \( \mathrm{f} \), where \( \mathrm{k} \) is a constant.
Suppose that the output values of \( \mathrm{g} \) are proportional over equal-length input-value intervals. This means that for a fixed interval length \( \mathrm{h} \),
\( \mathrm{ \displaystyle \dfrac{g(x+h)}{g(x)} = \text{constant} } \)
for all values of \( \mathrm{x} \) in the domain.
Since \( \mathrm{g(x) = f(x) + k} \), proportional change in \( \mathrm{g} \) implies that the underlying function \( \mathrm{f} \) must be based on multiplicative change, not additive change.
Therefore, if an additive transformation of a function has output values that change proportionally over equal-length input-value intervals, the original function \( \mathrm{f} \) must be an exponential function.
Key Idea
• Proportional change indicates exponential behavior
• Vertical shifts do not change whether a function is exponential
Example
A function \( \mathrm{g} \) is defined by
\( \mathrm{ \displaystyle g(x) = f(x) + 2 } \)
The values of \( \mathrm{g} \) satisfy
\( \mathrm{ \displaystyle \dfrac{g(x+1)}{g(x)} = 3 } \)
for all \( \mathrm{x} \). What can be concluded about \( \mathrm{f} \)?
▶️ Answer/Explanation
Since the ratio \( \mathrm{g(x+1)/g(x)} \) is constant, the output values of \( \mathrm{g} \) change proportionally.
Proportional change indicates exponential behavior.
Because \( \mathrm{g} \) differs from \( \mathrm{f} \) only by an additive constant, the underlying function \( \mathrm{f} \) must also be exponential.
Conclusion
The function \( \mathrm{f} \) is exponential.
Example
A function \( \mathrm{f} \) is unknown. Define
\( \mathrm{ \displaystyle g(x) = f(x) – 5 } \)
Suppose the output values of \( \mathrm{g} \) double whenever the input increases by 1.
What type of function is \( \mathrm{f} \)?
▶️ Answer/Explanation
Doubling over equal input intervals means the output values change proportionally.
This behavior characterizes exponential functions.
An additive transformation does not change the type of growth.
Conclusion
The function \( \mathrm{f} \) is exponential.
End Behavior of Exponential Functions
An exponential function in general form is given by
\( \mathrm{ \displaystyle f(x) = ab^x } \)
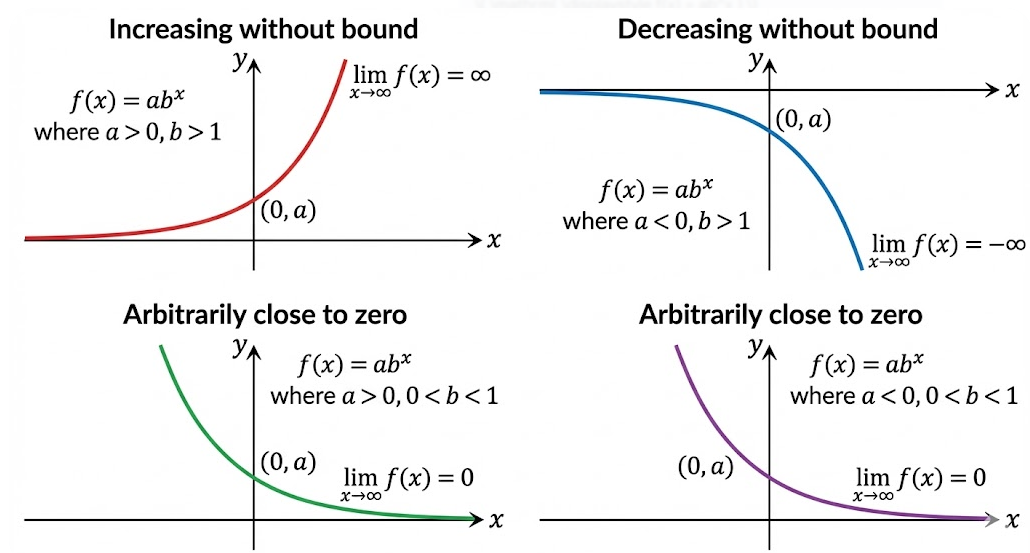
The end behavior of an exponential function describes what happens to the output values as the input values increase or decrease without bound.
Depending on the values of \( \mathrm{a} \) and \( \mathrm{b} \), the output values will either:
• Increase without bound
• Decrease without bound
• Get arbitrarily close to zero
This behavior can be expressed using limits.
For an exponential function in general form, one of the following is true:
\( \mathrm{ \displaystyle \lim_{x \to \pm\infty} ab^x = \infty } \)
\( \mathrm{ \displaystyle \lim_{x \to \pm\infty} ab^x = -\infty } \)
\( \mathrm{ \displaystyle \lim_{x \to \pm\infty} ab^x = 0 } \)
When the output values approach zero, the x-axis acts as a horizontal asymptote.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = 3 \cdot 2^x } \)
Describe the end behavior of the function.
▶️ Answer/Explanation
Here, \( \mathrm{a = 3 > 0} \) and \( \mathrm{b = 2 > 1} \).
As \( \mathrm{x \to \infty} \), the value of \( \mathrm{2^x} \) increases without bound.
\( \mathrm{ \displaystyle \lim_{x \to \infty} 3 \cdot 2^x = \infty } \)
As \( \mathrm{x \to -\infty} \), the value of \( \mathrm{2^x} \) approaches zero.
\( \mathrm{ \displaystyle \lim_{x \to -\infty} 3 \cdot 2^x = 0 } \)
Conclusion
The function grows without bound to the right and approaches zero to the left.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = -5(0.4)^x } \)
Describe the end behavior of the function.
▶️ Answer/Explanation
Here, \( \mathrm{a = -5 < 0} \) and \( \mathrm{0 < b = 0.4 < 1} \).
As \( \mathrm{x \to \infty} \), the value of \( \mathrm{(0.4)^x} \) approaches zero.
\( \mathrm{ \displaystyle \lim_{x \to \infty} -5(0.4)^x = 0 } \)
As \( \mathrm{x \to -\infty} \), the value of \( \mathrm{(0.4)^x} \) increases without bound, and the negative coefficient makes the output decrease without bound.
\( \mathrm{ \displaystyle \lim_{x \to -\infty} -5(0.4)^x = -\infty } \)
Conclusion
The function approaches zero on one end and decreases without bound on the other.
