AP Precalculus -2.4 Exponential Function Manipulation- Study Notes - Effective Fall 2023
AP Precalculus -2.4 Exponential Function Manipulation- Study Notes – Effective Fall 2023
AP Precalculus -2.4 Exponential Function Manipulation- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Rewrite exponential expressions in equivalent forms.
Key Concepts:
Product Property of Exponents and Exponential Transformations
Power Property of Exponents and Exponential Dilations
Negative Exponent Property
Exponential Unit Fractions and Roots
Product Property of Exponents and Exponential Transformations
The product property for exponents states that when multiplying powers with the same base, the exponents are added.
\( \mathrm{ \displaystyle b^m \cdot b^n = b^{(m+n)} } \)
This algebraic property has an important graphical interpretation for exponential functions.
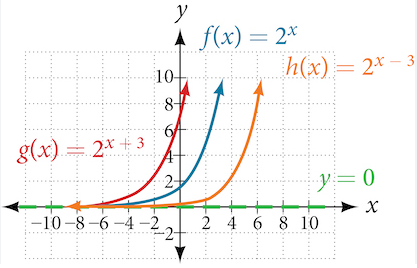
Consider an exponential function with a horizontal translation:
\( \mathrm{ \displaystyle f(x) = b^{(x+k)} } \)
Using the product property, this expression can be rewritten as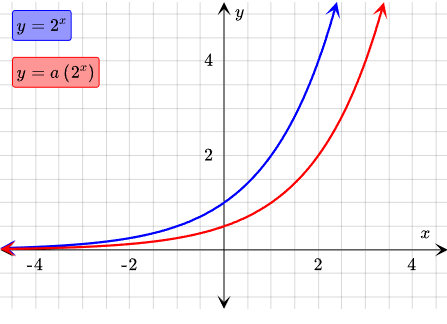
\( \mathrm{ \displaystyle b^{(x+k)} = b^x \cdot b^k } \)
Let \( \mathrm{a = b^k} \). Then the function becomes
\( \mathrm{ \displaystyle f(x) = ab^x } \)
This shows that a horizontal translation of an exponential function is equivalent to a vertical dilation.
Key Insight
• Horizontal shifts of exponential functions can be rewritten as vertical scalings
• This equivalence is unique to exponential functions because of exponent rules
Example
Rewrite the function
\( \mathrm{ \displaystyle f(x) = 2^{(x+3)} } \)
in the form \( \mathrm{ab^x} \).
▶️ Answer/Explanation
Apply the product property:
\( \mathrm{ \displaystyle 2^{(x+3)} = 2^x \cdot 2^3 } \)
Simplify:
\( \mathrm{ \displaystyle 2^{(x+3)} = 8 \cdot 2^x } \)
Conclusion
A horizontal shift left by 3 units is equivalent to a vertical stretch by a factor of 8.
Example
Rewrite the function
\( \mathrm{ \displaystyle f(x) = 5^{(x-2)} } \)
as a vertical dilation of \( \mathrm{5^x} \).
▶️ Answer/Explanation
Use the product property:
\( \mathrm{ \displaystyle 5^{(x-2)} = 5^x \cdot 5^{-2} } \)
Evaluate \( \mathrm{5^{-2}} \):
\( \mathrm{ \displaystyle 5^{-2} = \dfrac{1}{25} } \)
So the function becomes
\( \mathrm{ \displaystyle f(x) = \dfrac{1}{25} \cdot 5^x } \)
Conclusion
A horizontal shift right by 2 units is equivalent to a vertical shrink by a factor of \( \mathrm{\dfrac{1}{25}} \).
Power Property of Exponents and Exponential Dilations
The power property for exponents states that when a power is raised to another power, the exponents are multiplied.
\( \mathrm{ \displaystyle (b^m)^n = b^{(mn)} } \)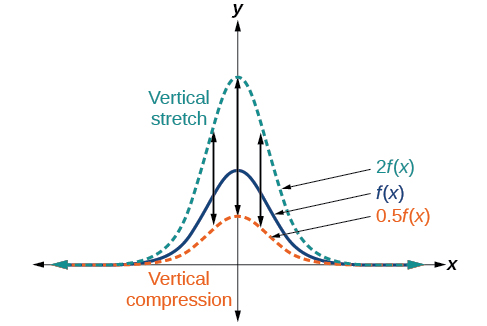
This algebraic property has an important graphical interpretation for exponential functions.
Consider an exponential function that includes a horizontal dilation:
\( \mathrm{ \displaystyle f(x) = b^{cx} } \)
Using the power property, this expression can be rewritten as
\( \mathrm{ \displaystyle b^{cx} = (b^c)^x } \)
This shows that a horizontal dilation of an exponential function is equivalent to a change in the base of the exponential function.
Here, \( \mathrm{b^c} \) is a constant base, and \( \mathrm{c \ne 0} \).
Key Insight
• Horizontal dilations compress or stretch the graph along the x-axis
• This effect can be represented by changing the base of the exponential function
Example
Rewrite the function
\( \mathrm{ \displaystyle f(x) = 3^{2x} } \)
as an exponential function with a new base.
▶️ Answer/Explanation
Apply the power property:
\( \mathrm{ \displaystyle 3^{2x} = (3^2)^x } \)
Simplify the base:
\( \mathrm{ \displaystyle (3^2)^x = 9^x } \)
Conclusion
A horizontal compression by a factor of \( \mathrm{\tfrac{1}{2}} \) is equivalent to changing the base from 3 to 9.
Example
Rewrite the function
\( \mathrm{ \displaystyle f(x) = 4^{\tfrac{x}{2}} } \)
as a function of the form \( \mathrm{(b^c)^x} \).
▶️ Answer/Explanation
Rewrite the exponent:
\( \mathrm{ \displaystyle 4^{\tfrac{x}{2}} = (4^{\tfrac{1}{2}})^x } \)
Simplify the base:
\( \mathrm{ \displaystyle (4^{\tfrac{1}{2}})^x = 2^x } \)
Conclusion
A horizontal stretch by a factor of 2 is equivalent to changing the base from 4 to 2.
Negative Exponent Property
The negative exponent property explains how to interpret powers with negative exponents.
It states that for any nonzero base \( \mathrm{b} \),
\( \mathrm{ \displaystyle b^{-n} = \dfrac{1}{b^n} } \)
This property shows that a negative exponent represents the reciprocal of the corresponding positive power.
In the context of exponential functions, negative exponents often arise when analyzing behavior for negative input values or when rewriting expressions into equivalent forms.
This property is especially useful for understanding exponential decay and end behavior.
Example
Rewrite the expression
\( \mathrm{ \displaystyle 2^{-4} } \)
using a positive exponent.
▶️ Answer/Explanation
Apply the negative exponent property:
\( \mathrm{ \displaystyle 2^{-4} = \dfrac{1}{2^4} } \)
Simplify:
\( \mathrm{ \displaystyle \dfrac{1}{16} } \)
Conclusion
A negative exponent moves the base to the denominator.
Example
Rewrite the exponential function
\( \mathrm{ \displaystyle f(x) = 5^{-x} } \)
in an equivalent form with a positive exponent.
▶️ Answer/Explanation
Apply the negative exponent property:
\( \mathrm{ \displaystyle 5^{-x} = \dfrac{1}{5^x} } \)
This form highlights that the function represents exponential decay.
Conclusion
Negative exponents correspond to reciprocals and are commonly used to model decreasing exponential behavior.
Exponential Unit Fractions and Roots
An exponential unit fraction is an exponent of the form \( \mathrm{\tfrac{1}{k}} \), where \( \mathrm{k} \) is a natural number.
For a positive base \( \mathrm{b} \), the exponential expression
\( \mathrm{ \displaystyle b^{\tfrac{1}{k}} } \)
represents the kth root of \( \mathrm{b} \), when that root exists.
That is,
\( \mathrm{ \displaystyle b^{\tfrac{1}{k}} = \sqrt[k]{\,b\,} } \)
This definition is consistent with the laws of exponents, since
\( \mathrm{ \displaystyle \left(b^{\tfrac{1}{k}}\right)^k = b } \)
Exponents involving unit fractions allow exponential expressions to be interpreted using radicals and extend exponent rules beyond whole-number powers.
Example
Evaluate the expression
\( \mathrm{ \displaystyle 16^{\tfrac{1}{2}} } \)
▶️ Answer/Explanation
A power of \( \mathrm{\tfrac{1}{2}} \) represents a square root:
\( \mathrm{ \displaystyle 16^{\tfrac{1}{2}} = \sqrt{16} } \)
Evaluate:
\( \mathrm{ \displaystyle \sqrt{16} = 4 } \)
Conclusion
The value of \( \mathrm{16^{\tfrac{1}{2}}} \) is 4.
Example
Evaluate the expression
\( \mathrm{ \displaystyle 27^{\tfrac{1}{3}} } \)
▶️ Answer/Explanation
A power of \( \mathrm{\tfrac{1}{3}} \) represents a cube root:
\( \mathrm{ \displaystyle 27^{\tfrac{1}{3}} = \sqrt[3]{27} } \)
Evaluate:
\( \mathrm{ \displaystyle \sqrt[3]{27} = 3 } \)
Conclusion
The value of \( \mathrm{27^{\tfrac{1}{3}}} \) is 3.
