AP Precalculus -2.6 Competing Function Models- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -2.6 Competing Function Models- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -2.6 Competing Function Models- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
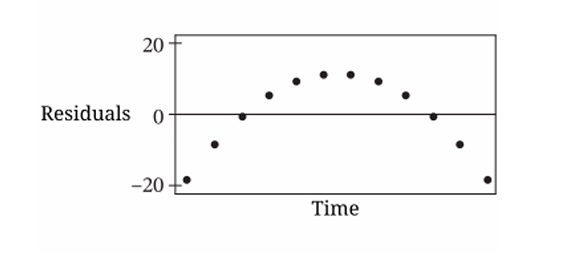
Question
(B) The linear model is not appropriate, because the graph of the residuals has more points above 0 than below 0.
(C) The linear model is appropriate, because there is a clear pattern in the graph of the residuals.
(D) The linear model is appropriate, because the positive residual farthest from 0 and the negative residual farthest from 0 are about the same distance, although more points are above 0 than below 0.
▶️ Answer/Explanation
If residuals show a clear pattern (curved shape, systematic deviation), the linear model is not appropriate.
From the description/figure (not shown here), residuals likely show a pattern.
✅ Answer: (A)
Question
| \( t \) (months) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \( P(t) \) (thousands) | 20 | 30 | 45 | 67.5 | 101.25 |
(A) \( y = 10t + 20 \)
(B) \( y = \frac{325}{16} t + 20 \)
(C) \( y = 20\left(\frac{2}{3}\right)^t \)
(D) \( y = 20\left(\frac{3}{2}\right)^t \)
▶️ Answer/Explanation
Observe the ratios of consecutive outputs:
\( 30/20 = 1.5 \), \( 45/30 = 1.5 \), \( 67.5/45 = 1.5 \), \( 101.25/67.5 = 1.5 \).
Constant ratio \( 1.5 = \frac{3}{2} \) indicates exponential growth: \( P(t) = a \cdot \left(\frac{3}{2}\right)^t \).
Using \( P(0) = 20 \) gives \( a = 20 \).
Thus \( P(t) = 20\left(\frac{3}{2}\right)^t \).
✅ Answer: (D)
Question
(B) The model produces an underestimate at \(A\) and an overestimate at \(B\). Based on the absolute values of the residuals, there is a greater error in the model with \(B\) than with \(A\).
(C) The model produces an overestimate at \(A\) and an underestimate at \(B\). Based on the absolute values of the residuals, there is a greater error in the model with \(A\) than with \(B\).
(D) The model produces an underestimate at \(A\) and an overestimate at \(B\). Based on the absolute values of the residuals, there is a greater error in the model with \(A\) than with \(B\).
▶️ Answer/Explanation
1. Understand Residuals:
\(\text{Residual} = \text{Actual} – \text{Predicted}\).
2. Analyze Point A (Residual = 1.3):
\(1.3 > 0\), so \(\text{Actual} > \text{Predicted}\). The model underestimated the value.
3. Analyze Point B (Residual = -2.5):
\(-2.5 < 0\), so \(\text{Actual} < \text{Predicted}\). The model overestimated the value.
4. Compare Errors:
The magnitude of the error is the absolute value of the residual.
Error at A: \(|1.3| = 1.3\)
Error at B: \(|-2.5| = 2.5\)
Since \(2.5 > 1.3\), the error is greater with B.
✅ Answer: (B)
Question
(B) \( y = \frac{325}{16}t + 20 \)
(C) \( y = 20\left(\frac{2}{3}\right)^t \)
(D) \( y = 20\left(\frac{3}{2}\right)^t \)
▶️ Answer/Explanation
Check ratios:
\( P(1)/P(0) = 30/20 = 1.5 \)
\( P(2)/P(1) = 45/30 = 1.5 \)
\( P(3)/P(2) = 67.5/45 = 1.5 \)
\( P(4)/P(3) = 101.25/67.5 = 1.5 \)
Constant ratio ⇒ exponential growth with base \( b = 1.5 = \frac{3}{2} \).
Initial value \( P(0) = 20 \) ⇒ \( a = 20 \).
Thus \( P(t) = 20 \left( \frac{3}{2} \right)^t \).
✅ Answer: (D)
Question
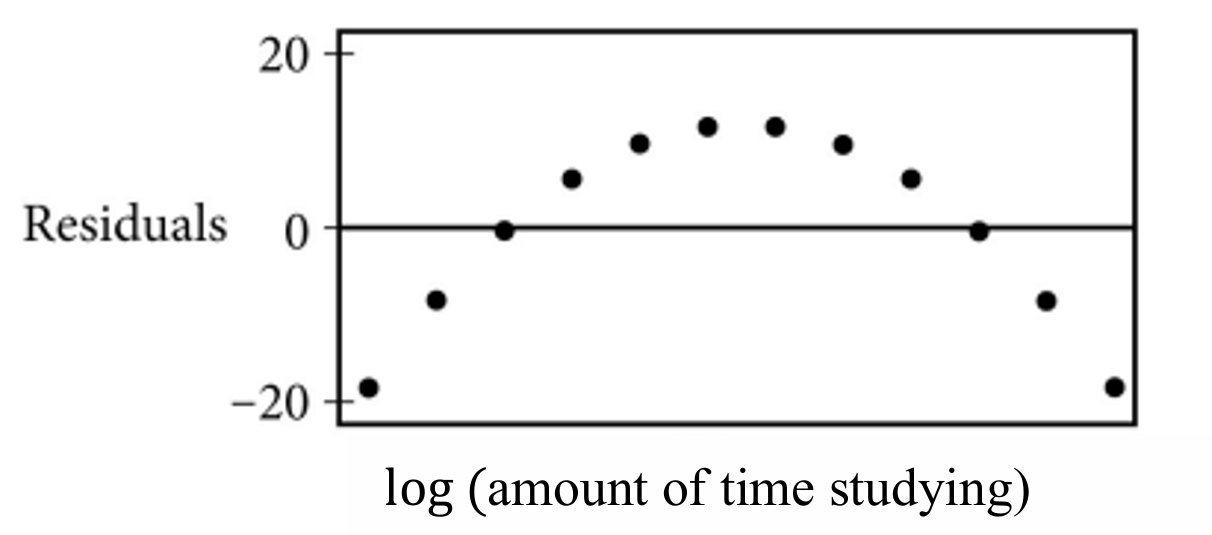
b. A logarithmic regression is not appropriate for this data set.
c. An exponential regression is appropriate for this data set.
d. A logarithmic regression is appropriate for this data set.
▶️ Answer/Explanation
The transformation used is $(x, \log y)$, which is the standard method to linearize an exponential model.
A residual plot shows the difference between the observed values and the values predicted by the regression line.
The provided residual plot shows a clear distinct curved pattern (a parabolic shape).
In statistics, a patterned residual plot indicates that the chosen model is not a good fit for the data.
Since the linear model was applied to $(x, \log y)$, this “bad fit” refers to the underlying exponential relationship.
Therefore, an exponential regression is not appropriate for this specific data set.
Correct Option: a
Question
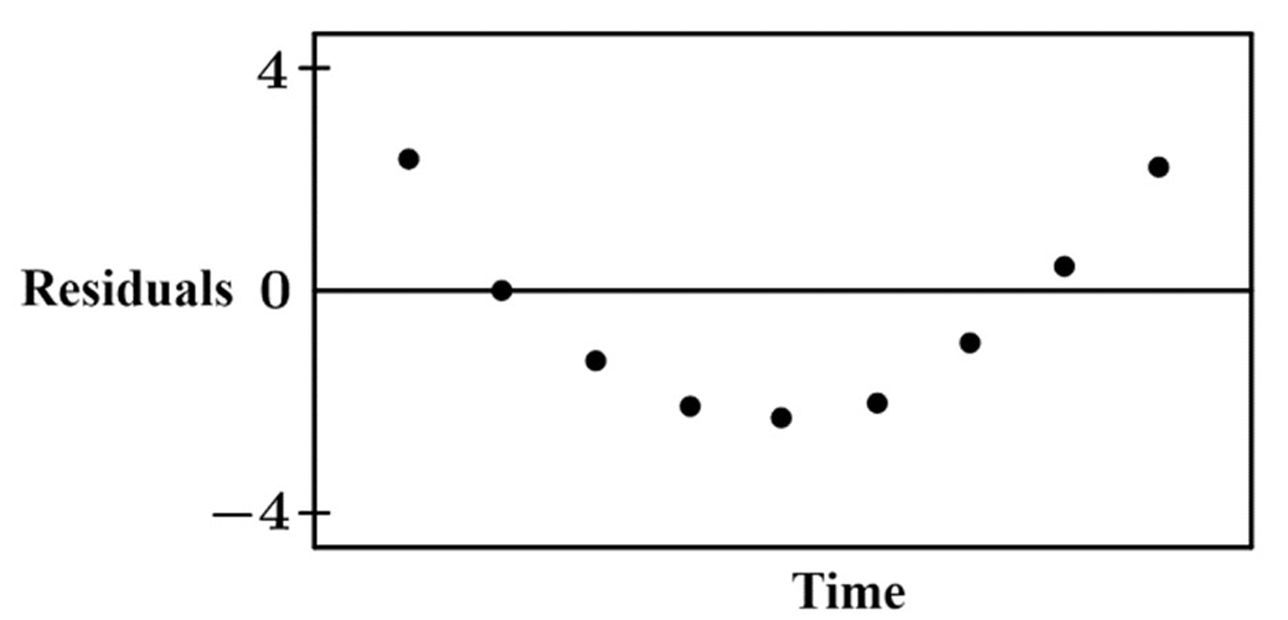
(B) A linear regression model is appropriate, but a quadratic regression may be a better model.
(C) A linear regression model is not appropriate, because the residuals do not show a linear pattern.
(D) A linear regression model is not appropriate, because the residuals show a clear pattern.
▶️ Answer/Explanation
The correct option is (D).
A residual plot should show a random scatter of points if a linear model is appropriate.
In this graph, the residuals exhibit a distinct $U$-shaped or curved pattern.
The presence of a non-random pattern indicates that the linear model fails to capture the underlying trend.
Therefore, the linear regression is not appropriate for this specific dataset.
This pattern suggests that a nonlinear model, such as a quadratic one, would be a better fit.
Option (D) correctly identifies that the pattern itself is the reason for the model’s inappropriateness.
Question
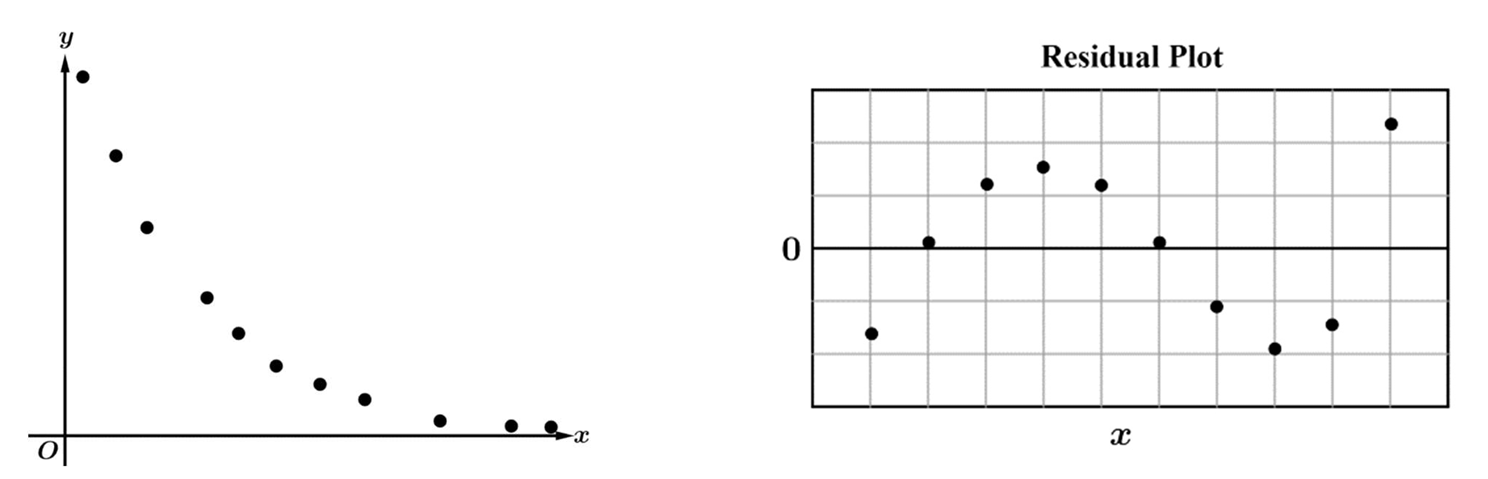
▶️ Answer/Explanation
The correct option is (B).
The residual plot shows a distinct curved, non-random pattern (a “U” or “inverted U” shape).
A curved pattern in a residual plot indicates that the model used is not appropriate for the data.
The original scatterplot shows a curved relationship that could be modeled by a quadratic function $y = ax^2 + bx + c$.
However, since the residuals are not randomly scattered around the $y = 0$ line, a quadratic fit fails to capture the full trend.
For a model to be appropriate, the residuals should be randomly distributed with no discernible pattern.
Therefore, the quadratic model was used, but the resulting pattern in the residuals proves it is not the best fit.
Question
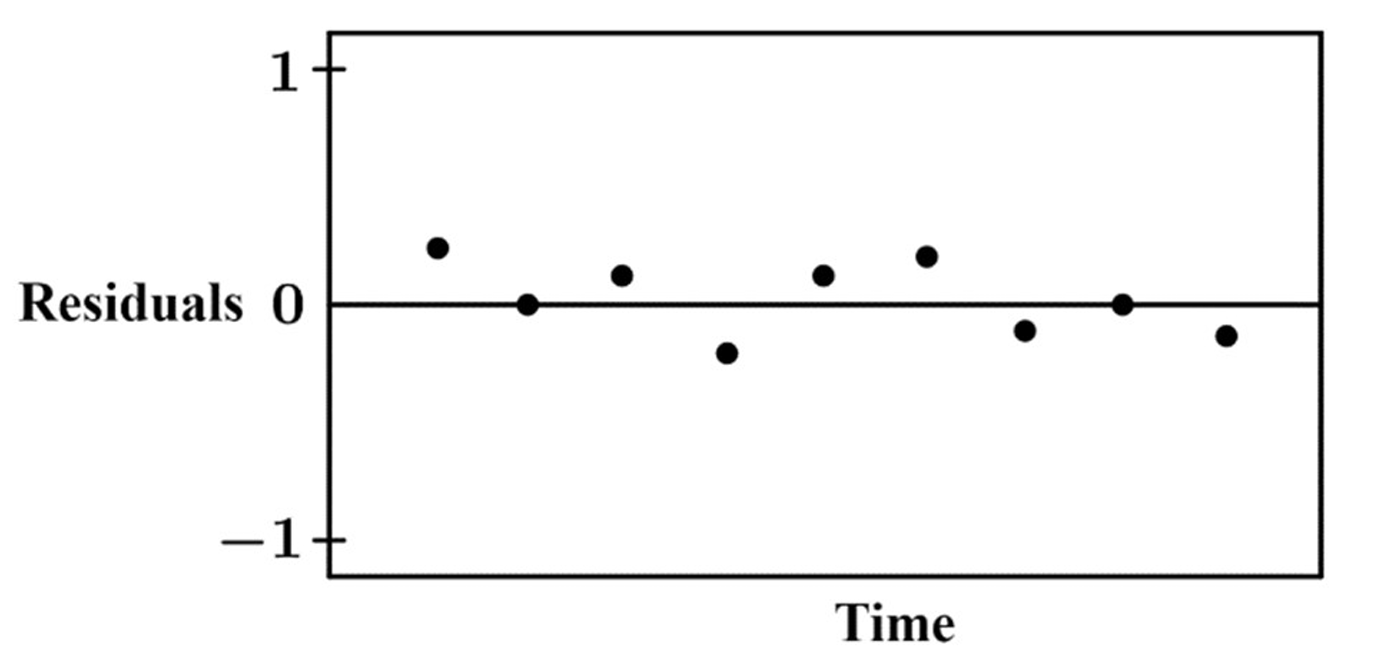
(B) The residual plot has no apparent pattern, so the exponential model was not appropriate.
(C) The residual plot displays a pattern, so the exponential model was appropriate.
(D) The residual plot displays a pattern, so the exponential model was not appropriate.
▶️ Answer/Explanation
The correct option is (A).
A residual is calculated as $\text{observed value} – \text{predicted value}$.
The provided residual plot shows points randomly scattered above and below the line $y = 0$.
There is no curved, U-shaped, or systematic pattern visible in the residuals.
A random distribution of residuals indicates that the chosen model fits the data well.
Since there is no apparent pattern, the exponential regression model is considered appropriate.
Therefore, the data confirms Mr. Passwater’s belief regarding the exponential growth.
Question

▶️ Answer/Explanation
Correct Answer: (C) $y = 4(3)^x$
An appropriate regression model is indicated by a residual plot with no clear pattern and points randomly dispersed around the horizontal axis.
The Linear Residual Plot shows a distinct U-shaped pattern, suggesting a linear model is inappropriate.
The Quadratic Residual Plot also shows a clear curved pattern, indicating the quadratic model does not fit well.
The Exponential Residual Plot shows a random distribution of points above and below the $x$-axis.
Since the exponential residual plot is the most random, an exponential model is the best fit.
Option (C) represents an exponential function, $y = 4(3)^x$, making it the appropriate choice.
Question
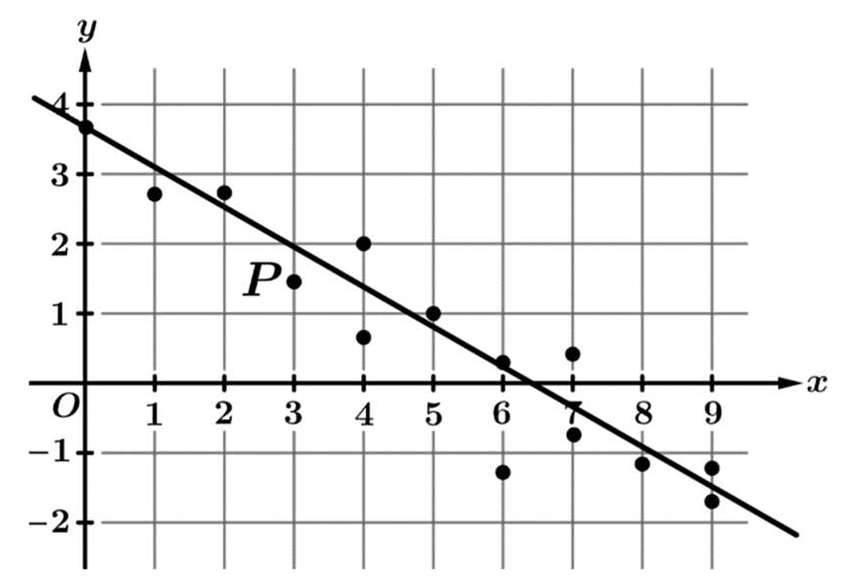
(B) $0.5$
(C) $1.5$
(D) $3$
▶️ Answer/Explanation
The residual is defined as the difference between the observed $y$-value and the predicted $\hat{y}$-value: $\text{Residual} = y – \hat{y}$.
Locate data point $P$ on the graph at the $x$-coordinate of $3$.
The actual $y$-value for point $P$ is $1.5$.
The predicted value $\hat{y}$ on the regression line at $x = 3$ is $2$.
Calculate the residual: $1.5 – 2 = -0.5$.
Therefore, the best estimate of the residual is $-0.5$.
The correct option is (A).
Question
(B) The residual of point $P$ is a negative value because the model produces an underestimate at point $P$.
(C) The residual of point $P$ is a positive value because the model produces an overestimate at point $P$.
(D) The residual of point $P$ is a positive value because the model produces an underestimate at point $P$.
▶️ Answer/Explanation
The correct option is (A).
Calculate the predicted value: $S(-1) = 3(2)^{-1} = 3(0.5) = 1.5$.
The actual $y$-coordinate of point $P$ is $1$.
The residual is calculated as $\text{Actual} – \text{Predicted} = 1 – 1.5 = -0.5$.
Since the residual is negative, the predicted value is greater than the actual value.
Therefore, the model produces an overestimate at point $P$.
Question
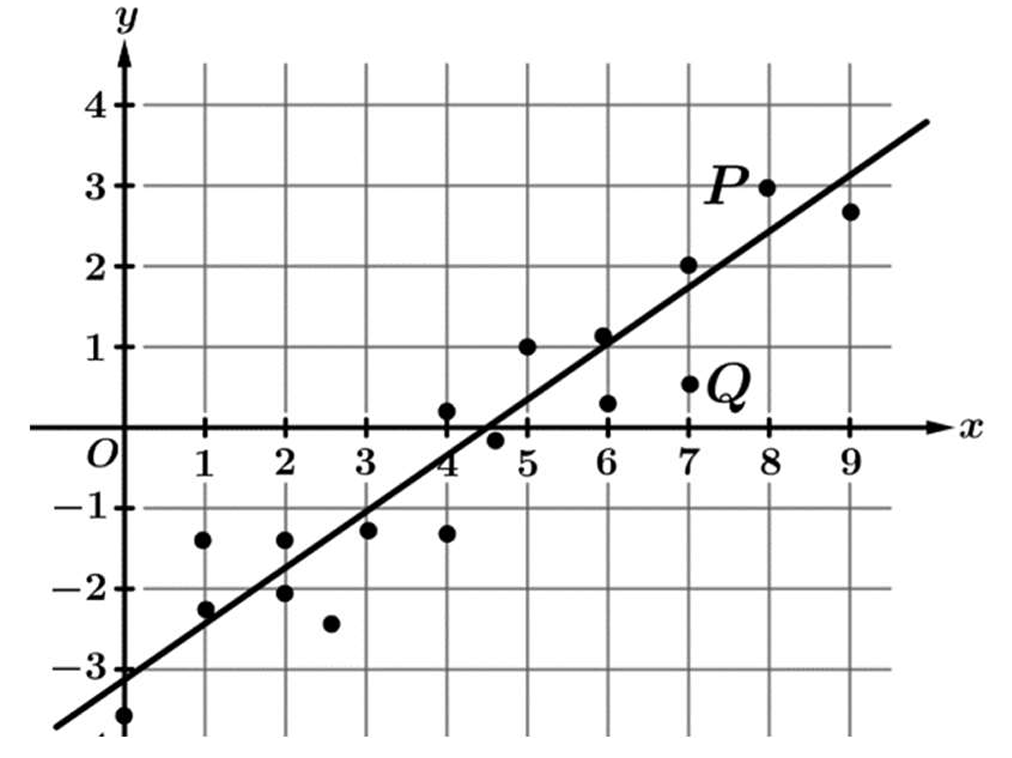
▶️ Answer/Explanation
Point \(P\) is above the regression line, meaning it has a positive residual.
Point \(Q\) is below the regression line, meaning it has a negative residual.
Since one is positive and one is negative, the residuals have opposite signs.
The vertical distance from \(Q\) to the line is visually larger than the distance from \(P\) to the line.
The absolute value of a residual represents the magnitude of error for that point.
Therefore, there is a greater error in the model for point \(Q\) than for point \(P\).
This matches statement (D).
Question

▶️ Answer/Explanation
The differences between consecutive \(P(t)\) values (\(30-20=10\), \(45-30=15\)) are not constant, so the model is not linear (eliminates A and B).
Calculate the ratio of consecutive terms: \(\frac{30}{20} = 1.5\) and \(\frac{45}{30} = 1.5\).
Since the ratio is constant at \(1.5\) or \(\frac{3}{2}\), the data represents an exponential growth model.
An exponential function has the form \(y = a(b)^t\), where \(a\) is the initial value and \(b\) is the growth factor.
From the table, at \(t=0\), the value is \(20\), so the initial value \(a = 20\).
The growth factor \(b\) is the constant ratio \(\frac{3}{2}\).
Therefore, the function is \(y = 20 \left(\frac{3}{2}\right)^t\), which corresponds to option (D).
Question
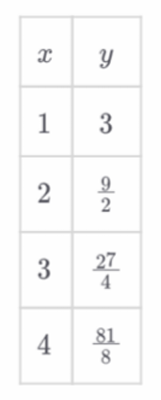
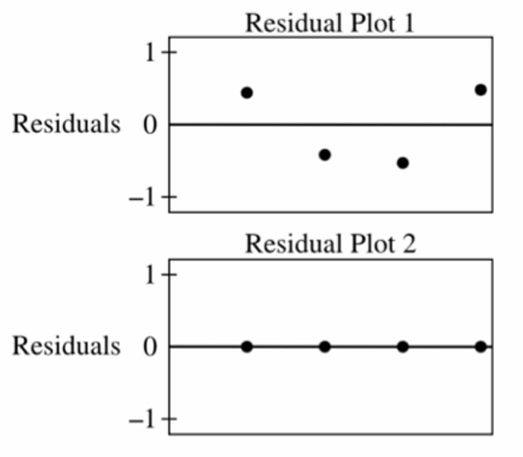
(B) A linear model is more appropriate for these data, and Residual Plot 2 corresponds to the linear regression.
(C) An exponential model is more appropriate for these data, and Residual Plot 1 corresponds to the exponential regression.
(D) An exponential model is more appropriate for these data, and Residual Plot 2 corresponds to the exponential regression.
▶️ Answer/Explanation
The correct answer is (D).
Analysis of the $y$-values shows a constant ratio: $\frac{9/2}{3} = \frac{27/4}{9/2} = \frac{81/8}{27/4} = 1.5$.
A constant ratio indicates that the data is perfectly exponential.
Residual Plot 2 shows all residuals are exactly $0$, meaning the model fits the data perfectly.
Therefore, the exponential model is the most appropriate for this data set.
Residual Plot 2 corresponds to this perfect exponential fit.
Residual Plot 1 shows a pattern, which usually indicates an inappropriate model (likely the linear one).
Question (Calc allowed)
▶️ Answer/Explanation
Set up the equation where the logarithmic model exceeds the linear model by $0.1$: $k(t) = m(t) + 0.1$.
Substitute the given functions: $14 – 2.885 \ln t = (-t + 14) + 0.1$.
Simplify the equation to: $-2.885 \ln t = -t + 0.1$.
Rearrange to form the function: $f(t) = t – 2.885 \ln t – 0.1 = 0$.
Use a graphing calculator to find the intersection of $y = 14 – 2.885 \ln t$ and $y = -t + 14.1$.
The first intersection point for $t \geq 2$ occurs at $t \approx 2.289$.
Thus, the correct option is (D).
Question

(B) $f$ is best modeled by an exponential function, because the output values change proportionately as input values increase in equal-length intervals.
(C) $f$ is best modeled by a logarithmic function, because the input values change proportionately as output values increase in equal-length intervals.
(D) $f$ is best modeled by a logarithmic function, because the output values change proportionately as input values increase in equal-length intervals.
▶️ Answer/Explanation
The correct option is (C).
As the output values $f(x)$ increase by a constant addition of $2$ ($2, 4, 6, 8, 10$),
the corresponding input values $x$ change by a constant factor of $1/2$ ($80, 40, 20, 10, 5$).
This relationship defines a logarithmic function, where inputs change geometrically while outputs change arithmetically.
In an exponential function, the roles are reversed: inputs change arithmetically and outputs change geometrically.
Therefore, $f$ is logarithmic because input values change proportionately as output values increase in equal-length intervals.
The specific model for this data is $f(x) = \log_{1/\sqrt{2}}(x/80) + 2$.
Question
(B) $0.172$
(C) $0.540$
(D) $1.002$
▶️ Answer/Explanation
Find $L(x)$: Slope $m = \frac{6-2}{1-0} = 4$, so $L(x) = 4x + 2$.
Find $E(x)$: Form $y = ab^x$. At $x=0$, $a=2$; at $x=1$, $2b=6 \implies b=3$. So $E(x) = 2(3^x)$.
Define $f(x) = 4x + 2 – 2(3^x)$.
To find the maximum, set $f'(x) = 4 – 2(3^x)\ln(3) = 0$.
Solve for $x$: $3^x = \frac{2}{\ln(3)} \implies x = \frac{\ln(2/\ln(3))}{\ln(3)} \approx 0.544$.
Calculate $f(0.544) = 4(0.544) + 2 – 2(3^{0.544}) \approx 4.176 – 4.004 = 0.172$.
The correct option is (B).
Question
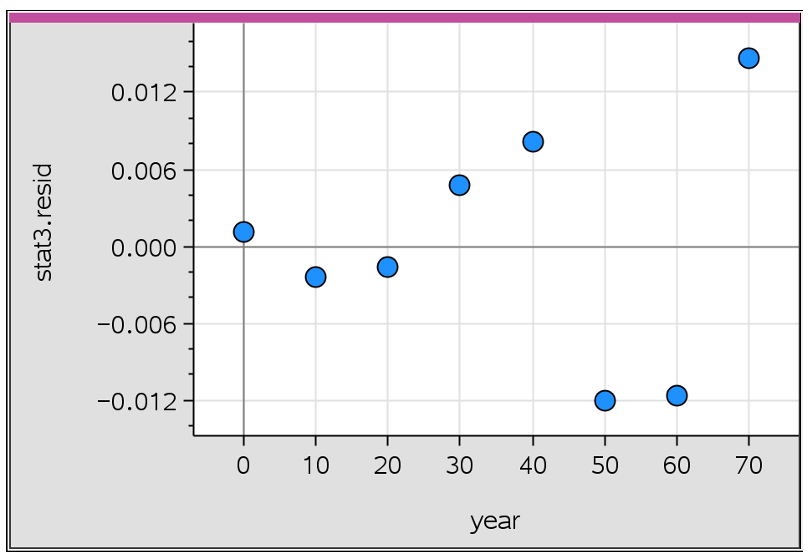
▶️ Answer/Explanation
The correct option is (D).
The residual plot clearly shows a distinct $U$-shaped curve rather than a random scatter.
A visible pattern in a residual plot indicates that the chosen model (exponential) does not capture the underlying trend.
In statistics, a model is considered “appropriate” only if its residuals are randomly distributed around the horizontal axis.
Since a clear non-linear pattern exists, the exponential regression is an inappropriate fit for this specific data set.
Therefore, the presence of a pattern confirms the model’s inadequacy.
Question
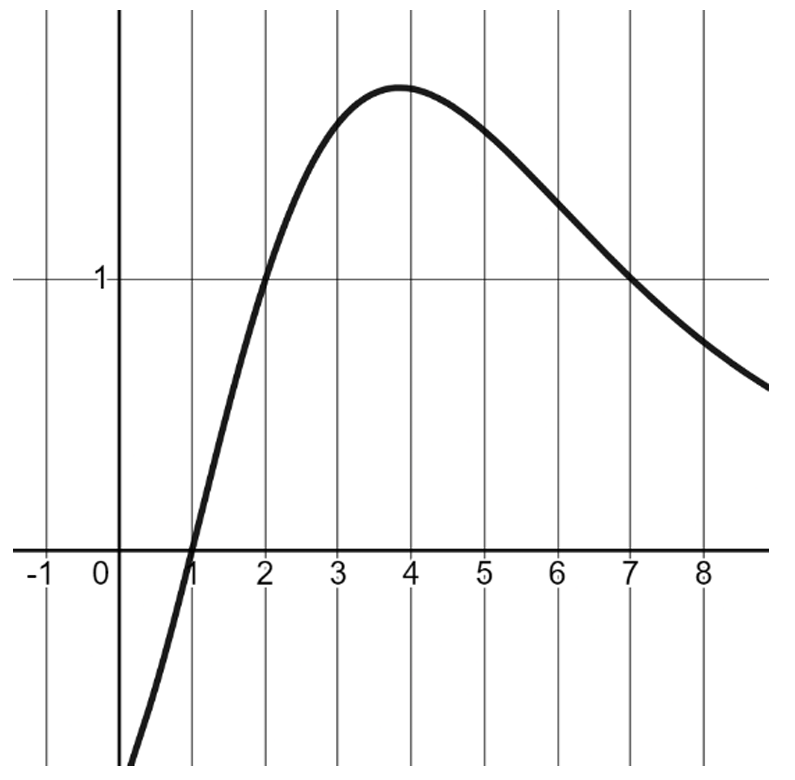
Most-appropriate topic codes (CED):
• TOPIC 1.10: Rational Functions and Holes — part (A)ii
• TOPIC 1.7: Rational Functions and End Behavior — part (B)i
• TOPIC 1.9: Rational Functions and Vertical Asymptotes — part (B)ii
• TOPIC 2.10: Logarithmic Function Context and Data Modeling — part (C)
▶️ Answer/Explanation
(A)
i. The graph of \( f(x) \) shows that \( f(2) \approx 1 \), so \( f^{-1}(1) \approx 2 \). From the table, \( g(2) = 1 \). Thus, \( g(f^{-1}(1)) \approx 1 \).
Since \( f(x) \) is continuous and increasing, the inverse is defined for values in its range.
The estimate is a single value, \( 1 \), as the graph aligns precisely with the point. No other values exist due to the strictly increasing nature of \( f(x) \).
ii. The graph of \( f(x) \) crosses zero at \( x=1 \), so \( f(1)=0 \), and from the table, \( g(1)=0 \).
Thus, \( h(1) \) is undefined (\( 0/0 \) form).
The limit as \( x \to 1 \) of \( h(x) \) exists and equals \( 1 \), since both \( g(x) \) and \( f(x) \) resemble \( \log_2(x) \), making \( h(x)=1 \) elsewhere.
This indicates a removable discontinuity at \( x=1 \). No other discontinuities for \( x>0 \), as \( f(x) \neq 0 \) elsewhere in the domain.
The location is \( x=1 \), type: removable.
(B)
i. As \( x \to \infty \), \( \ln(x) \to \infty \), so \( 4.99 – \ln(x) \to -\infty \), and \( \frac{1}{4.99 – \ln(x)} \to 0^- \).
The term \( e^{2 \sin(\sqrt{x})} \) oscillates between \( e^{-2} \) and \( e^{2} \), remaining bounded.
By the squeeze theorem, since the amplitude approaches \( 0 \), \( \lim_{x \to \infty} j(x) = 0 \).
The end behavior is that \( j(x) \) approaches \( 0 \). The limit exists.
ii. As \( x \to 0^+ \), \( \ln(x) \to -\infty \), so \( 4.99 – \ln(x) \to +\infty \), and \( \frac{1}{4.99 – \ln(x)} \to 0^+ \).
Also, \( \sqrt{x} \to 0^+ \), \( \sin(\sqrt{x}) \to 0^+ \), so \( e^{2 \sin(\sqrt{x})} \to e^0 = 1 \).
Thus, \( j(x) \to 0 \cdot 1 = 0 \).
The limit is \( \lim_{x \to 0^+} j(x) = 0 \).
No vertical asymptote at \( x=0 \), as the function approaches a finite value, not \( \pm \infty \).
(C)
The table shows \( g(x) \) values: at \( x=0.5, 1, 2, 4, 7, 8 \), \( g(x)=-1, 0, 1, 2, 2.807, 3 \).
When \( x \) doubles (\( 0.5 \) to \( 1 \), \( 1 \) to \( 2 \), \( 2 \) to \( 4 \), \( 4 \) to \( 8 \)), \( \Delta g = +1 \) consistently.
This pattern matches logarithmic functions, where outputs increase by a constant for multiplicative input changes.
Linear would require constant \( \Delta g \) for constant \( \Delta x \), but \( \Delta x \) varies while \( \Delta g =1 \) for doublings.
Quadratic would show constant second differences, but here first differences are not constant.
Exponential would show constant ratios in outputs for additive input changes, which does not fit.
Thus, best modeled by a logarithmic function like \( g(x) = \log_2(x) \).
Question
Part A
Part B
Part C
▶️ Answer/Explanation
Part A
(i)
Using the data $M(6) = 508.67$ and $M(12) = 517.50$:
$ab^{(6/12)} = 508.67$ (or $ab^{0.5} = 508.67$)
$ab^{(12/12)} = 517.50$ (or $ab = 517.50$)
(ii)
Divide the second equation by the first: $\frac{ab}{ab^{0.5}} = \frac{517.50}{508.67}$
$b^{0.5} \approx 1.017359…$
$b \approx (1.017359…)^2 \approx 1.035019…$
Using $ab = 517.50 \implies a = \frac{517.50}{1.035019…} \approx 500$
Final values: $a \approx 500.00$ and $b \approx 1.035$
Part B
(i)
$t = -2$ falls in the interval $-10 \le t < 0$, so $M(-2) = 500$.
$t = 12$ is given as $M(12) = 517.50$.
Average Rate of Change $= \frac{M(12) – M(-2)}{12 – (-2)}$
$= \frac{517.50 – 500}{12 + 2}$
$= \frac{17.50}{14} = 1.25$ dollars per month.
(ii)
The linear estimate $A(t)$ uses the point $(12, 517.50)$ and slope $1.25$.
$A(20) = M(12) + 1.25(20 – 12)$
$A(20) = 517.50 + 1.25(8)$
$A(20) = 517.50 + 10 = 527.50$ dollars.
(iii)
The model $M(t)$ for $t \ge 0$ is an exponential function ($b > 1$), which is concave up.
The estimate $A(t)$ is a linear function (a secant line).
Since $M(t)$ is increasing at an increasing rate (exponential growth), the linear model will fall further behind the actual values as $t$ increases.
Part C
The model is only valid as long as the account is open.
Setting $M(t) = 565$ allows us to solve for the maximum value of $t$.
$500(1.035)^{(t/12)} = 565$
This value of $t$ serves as the upper bound (maximum) for the domain of the model $M$.
Question
(A) (i) Use the given data to write two equations that can be used to find the values for constants \(a\) and \(b\) in the expression for \(R(t)\).
(ii) Find the values for \(a\) and \(b\) as decimal approximations.
(B) (i) Use the given data to find the average rate of change in the number of students that have heard the rumor, in students per hour, from \(t=2\) to \(t=6\) hours. Express your answer as a decimal approximation. Show the computations that lead to your answer.
(ii) Interpret the meaning of your answer from (i) in the context of the problem.
(iii) Consider the values that result from using the average rate of change found in (i) to estimate the number of students that have heard the rumor for times \(t=p\) hours, where \(0 < p < 6\). Are these estimates less than or greater than the number of students predicted by the model \(R\) for times \(t=p\) hours? Explain your reasoning using characteristics of the average rate of change and characteristics of the model \(R\).
▶️ Answer/Explanation
Part (A)
(i) Writing the equations:
We are given the following data points:
• At \(t=2\), \(R(2) = 15\).
• At \(t=6\), \(R(6) = 67\).
For \(t=2\), since \(0 \le 2 < 6\), we use the first part of the piecewise function: \(R(t) = 7(a)^{t/2}\).
$$15 = 7(a)^{2/2} \quad \Rightarrow \quad 15 = 7a^1$$
Equation 1: \(15 = 7a\)
For \(t=6\), since \(t \ge 6\), we use the second part of the piecewise function: \(R(t) = -213.29 + b \ln t\).
Equation 2: \(67 = -213.29 + b \ln(6)\)
(ii) Finding the values for \(a\) and \(b\):
From Equation 1:
$$a = \frac{15}{7} \approx 2.1428$$
From Equation 2:
$$67 + 213.29 = b \ln(6)$$
$$280.29 = b \ln(6)$$
$$b = \frac{280.29}{\ln(6)} \approx \frac{280.29}{1.79176} \approx 156.4328$$
Answer: \(a \approx 2.143\), \(b \approx 156.433\)
Part (B)
(i) Average Rate of Change:
The formula for the average rate of change from \(t=2\) to \(t=6\) is:
$$\text{Avg Rate} = \frac{R(6) – R(2)}{6 – 2}$$
Substituting the given values (\(R(6)=67\) and \(R(2)=15\)):
$$\text{Avg Rate} = \frac{67 – 15}{4} = \frac{52}{4} = 13$$
Answer: 13 students per hour.
(ii) Interpretation:
On average, the number of students who have heard the rumor increases by 13 students per hour between the 2nd hour and the 6th hour.
(iii) Estimates vs. Model Prediction:
Answer: The estimates are greater than the number of students predicted by the model.
Reasoning:
• On the interval \(0 < t < 6\), the function \(R(t) = 7(a)^{t/2}\) is an exponential growth function with a base greater than 1.
• Exponential growth functions are concave up (the rate of change is increasing).
• The average rate of change corresponds to the slope of the secant line connecting the points at \(t=2\) and \(t=6\).
• For a concave up curve, the secant line lies above the curve on the interval between the two points. Therefore, linear estimates based on the average rate (secant line) will be greater than the actual function values.
Part (C)
The range values (outputs) of \(R(t)\) represent the number of students. In the context of the problem, this range must be limited in two ways:
1. Population Cap: The number of students who heard the rumor cannot exceed the total student population of the school.
2. Discrete Values: You cannot have a fraction of a student, so strictly speaking, the context implies the range should consist of whole numbers (non-negative integers).
Question
▶️ Answer/Explanation
(A)(i) Equations
Substituting the points \((1, 3)\) and \((5, 89)\) into \(H(t) = ab^t\):
1. \(3 = ab^1\) (or \(3 = ab\))
2. \(89 = ab^5\)
(A)(ii) Values for a and b
Dividing equation 2 by equation 1: \(\frac{ab^5}{ab} = \frac{89}{3} \implies b^4 = 29.67\).
Solving for \(b\): \(b = (29.67)^{0.25} \approx 2.33\).
Solving for \(a\): \(a = \frac{3}{2.33} \approx 1.29\).
(B)(i) Average Rate of Change
\(\text{Rate} = \frac{H(5) – H(1)}{5 – 1} = \frac{89 – 3}{4} = \frac{86}{4} = 21.5\)
Answer: 21.5 feet per week.
(B)(ii) Interpretation
The answer indicates that between the first and fifth weeks, the bamboo tree grew at an average speed of 21.5 feet per week.
(B)(iii) Comparison
Greater. The function represents exponential growth (\(b > 1\)), which is concave up. This means the rate of growth increases over time, so the rate after week 5 will be steeper than the rate before week 5.
(C) Confidence
\(t = 4\) weeks.
The biologists should be more confident in \(t=4\) because it is an interpolation (within the observed data range). \(t=11\) is an extrapolation; biological growth cannot remain exponential indefinitely, so the model is likely inaccurate that far out.