AP Precalculus -2.8 Inverse Functions- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -2.8 Inverse Functions- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -2.8 Inverse Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
Question
(B) \( \log_2(4x) + 3 \)
(C) \( \log_2\left(\frac{x}{4}\right) + 3 \)
(D) \( \log_2\left(\frac{x-3}{4}\right) \)
▶️ Answer/Explanation
To find the inverse, solve \( y = 4 \cdot 2^{(x-3)} \) for \( x \):
Divide by 4: \( \frac{y}{4} = 2^{(x-3)} \)
Take \(\log_2\): \( \log_2\left(\frac{y}{4}\right) = x – 3 \)
Thus \( x = \log_2\left(\frac{y}{4}\right) + 3 \)
Swap \( x \) and \( y \): \( g(x) = \log_2\left(\frac{x}{4}\right) + 3 \)
✅ Answer: (C)
Question
(B) \( \sqrt{4 – x^2} \) for \( -2 \leq x \leq 0 \)
(C) \( -\sqrt{4 – x^2} \) for \( 0 \leq x \leq 2 \)
(D) \( \sqrt{4 – x^2} \) for \( 0 \leq x \leq 2 \)
▶️ Answer/Explanation
Let \( y = \sqrt{4 – x^2} \) with \( -2 \leq x \leq 0 \) and \( 0 \leq y \leq 2 \).
Solve for \( x \): \( y^2 = 4 – x^2 \) ⇒ \( x^2 = 4 – y^2 \) ⇒ \( x = -\sqrt{4 – y^2} \) (negative because \( x \leq 0 \)).
Swap \( x \) and \( y \): \( f^{-1}(x) = -\sqrt{4 – x^2} \).
The domain of \( f^{-1} \) is the range of \( f \), which is \( 0 \leq x \leq 2 \).
✅ Answer: (C)
Question
▶️ Answer/Explanation
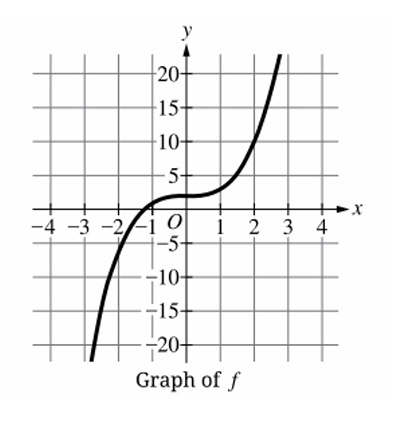
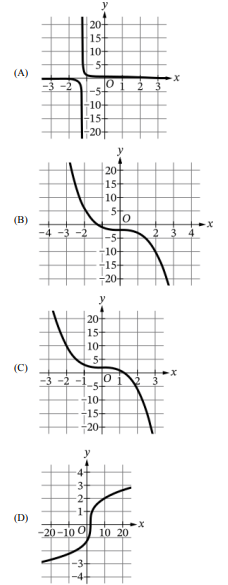
The graph of \( y = f^{-1}(x) \) is the reflection of the graph of \( y = f(x) \) across the line \( y = x \).
From the given figure, \( f \) appears to be a curve that increases and spans large \( y \)-values for small \( x \) changes.
The inverse should thus have large \( x \)-values for small \( y \) changes, resembling the shape in option (D) where the axes appear swapped.
✅ Answer: (D)
Question
(B) \( f^{-1}(x) = \sqrt{\frac{x}{4}} – 3 \) for \( x \geq 0 \)
(C) \( f^{-1}(x) = \sqrt{\frac{x-3}{4}} \) for \( x \geq 3 \)
(D) \( f^{-1}(x) = \frac{\sqrt{x-3}}{4} \) for \( x \geq 3 \)
▶️ Answer/Explanation
Let \( y = 4x^2 + 3 \), \( x \geq 0 \), so \( y \geq 3 \).
Solve for \( x \): \( y – 3 = 4x^2 \) ⇒ \( x^2 = \frac{y-3}{4} \) ⇒ \( x = \sqrt{\frac{y-3}{4}} \) (positive root since \( x \geq 0 \)).
Swap \( x \) and \( y \): \( f^{-1}(x) = \sqrt{\frac{x-3}{4}} \) for \( x \geq 3 \).
✅ Answer: (C)
Question
▶️ Answer/Explanation
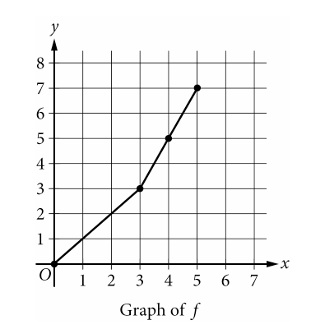
From the graph, \( f \) is increasing and its maximum output is \( y = 7 \) at \( x = 5 \) (endpoint).
Since \( g \) is the inverse of \( f \), the domain of \( g \) is the range of \( f \), and the range of \( g \) is the domain of \( f \).
The range of \( g \) is \( [0,5] \), so the maximum value of \( g \) is 5, which occurs when the input to \( g \) is 7 because \( f(5) = 7 \) ⇒ \( g(7) = 5 \).
✅ Answer: (C)
Question
▶️ Answer/Explanation
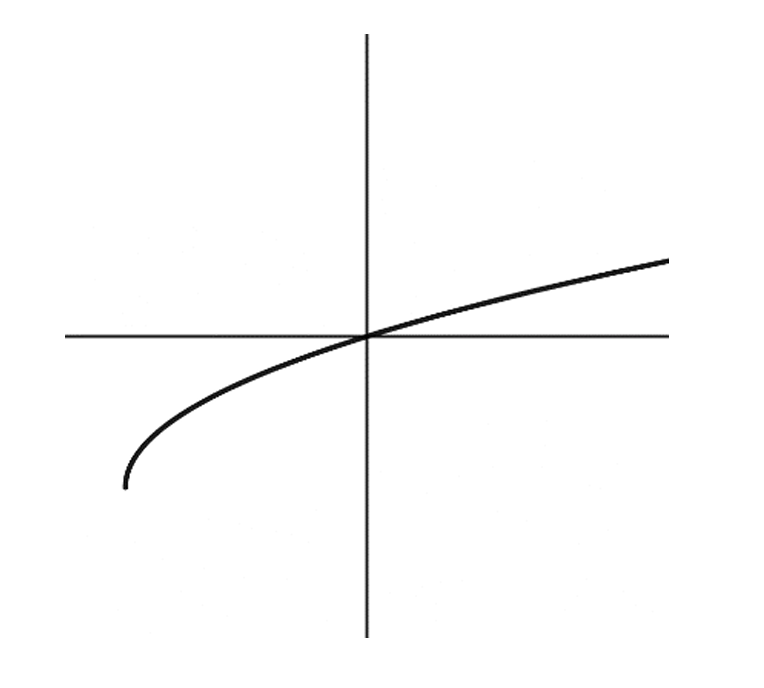
The inverse of a function $f(x)$ is found by reflecting its graph across the line $y = x$.
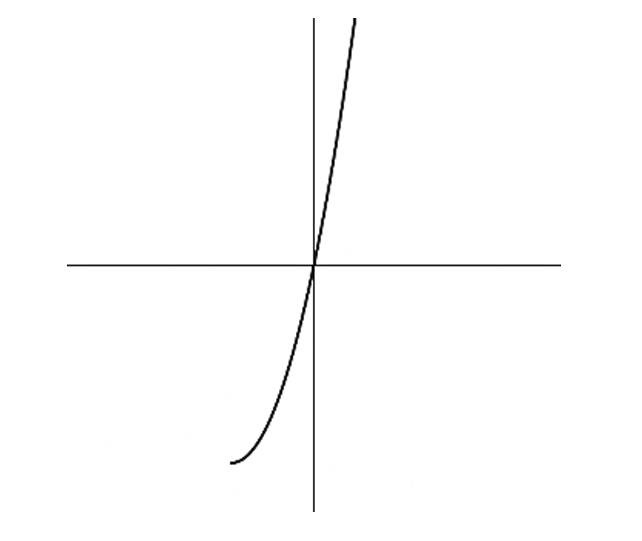
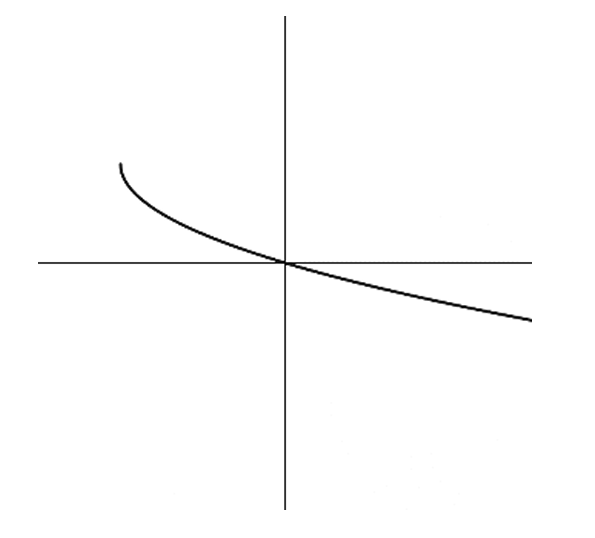
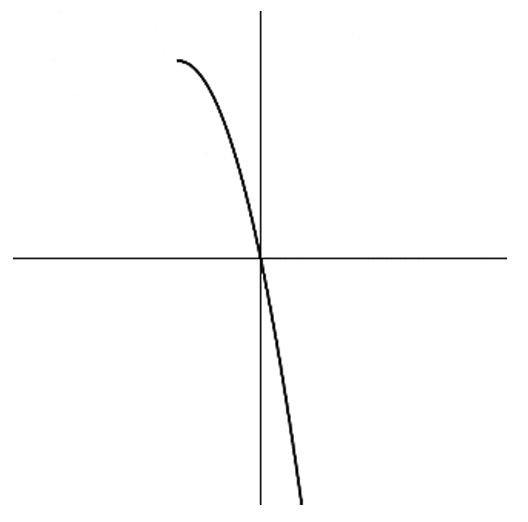
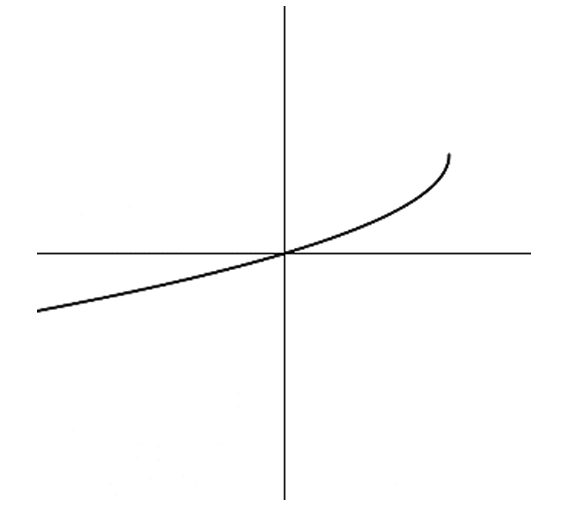
In the original graph, the curve passes through the origin $(0,0)$.
The original function has a slow horizontal growth in the first quadrant and a steep drop in the third quadrant.
When reflected across $y = x$, the horizontal behavior becomes vertical and the vertical becomes horizontal.
This results in a graph that is steep in the first quadrant and flattens out in the third quadrant.
Comparing the choices, Option (a) correctly represents this reflection.
Therefore, the correct representation of the inverse $f^{-1}(x)$ is a.
Question
▶️ Answer/Explanation
The function \(P\) takes time as the input and outputs the amount of water.
Therefore, the inverse function \(P^{-1}\) must swap these roles: it takes the amount of water as the input and outputs time.
Since \(P\) is an increasing function (more time equals more water), its inverse must also be increasing.
Logically, to reach a greater amount of water (input for \(P^{-1}\)), a greater amount of time (output for \(P^{-1}\)) is required.
Thus, \(P^{-1}\) is an increasing function of the amount of water in the pool.
This description matches option (C).
Question
▶️ Answer/Explanation
To find the value of \( g^{-1}(3) \), we need to find the value of \( x \) such that \( g(x) = 3 \).
First, substitute \( f(x) \) into the given equation for \( g(x) \):
\( g(x) = \frac{1}{2}\log_5(x+3) + 2 \)
Set the equation equal to 3 and solve for \( x \):
\( \frac{1}{2}\log_5(x+3) + 2 = 3 \)
Subtract 2 from both sides: \( \frac{1}{2}\log_5(x+3) = 1 \)
Multiply both sides by 2: \( \log_5(x+3) = 2 \)
Convert the logarithmic equation to exponential form: \( x + 3 = 5^2 \)
Solve for \( x \): \( x = 25 – 3 = 22 \).
Therefore, the correct option is (D).
Question
▶️ Answer/Explanation
Question
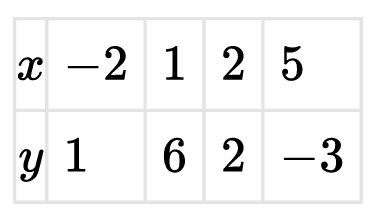
The table gives values for the invertible function $y = f(x)$ for selected values of $x$. Which of the following input-output pairs describes $f^{-1}$?
(A) 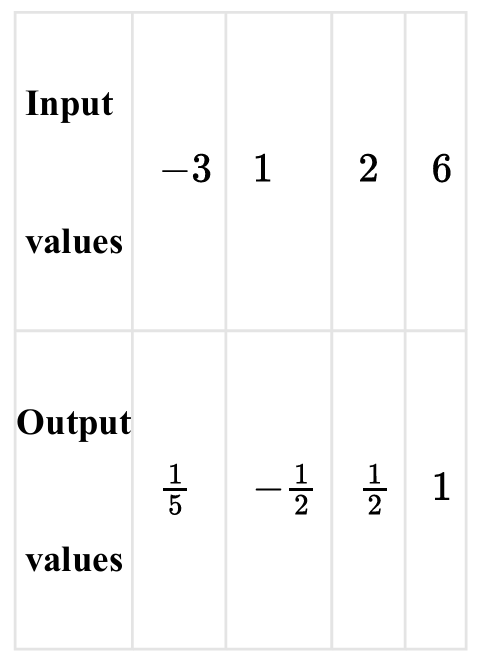
(B) 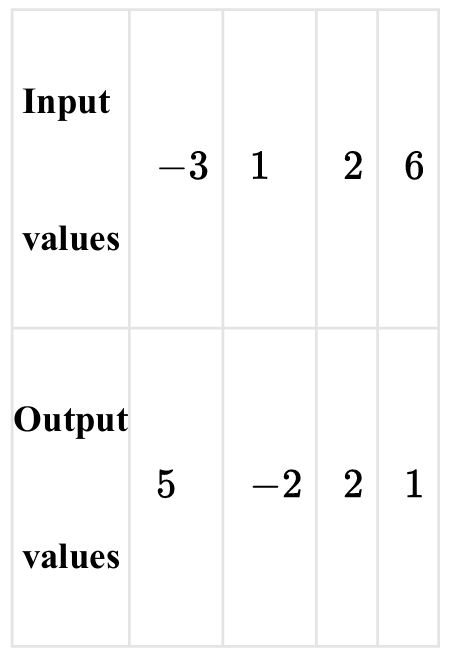
(C) 
(D) 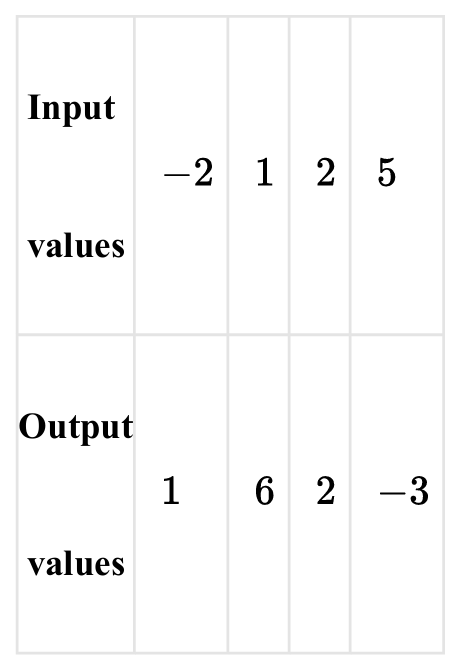
▶️ Answer/Explanation
The inverse function $f^{-1}$ swaps the inputs and outputs of the original function $f$.
From the table, the original pairs $(x, y)$ are $(-2, 1)$, $(1, 6)$, $(2, 2)$, and $(5, -3)$.
The inverse pairs $(y, x)$ must be $(1, -2)$, $(6, 1)$, $(2, 2)$, and $(-3, 5)$.
Sorting these by input value, we get: $(-3, 5)$, $(1, -2)$, $(2, 2)$, and $(6, 1)$.
Option (B) lists these input values $\{-3, 1, 2, 6\}$ with corresponding outputs $\{5, -2, 2, 1\}$.
Therefore, (B) is the correct description of the inverse function $f^{-1}$.
Question
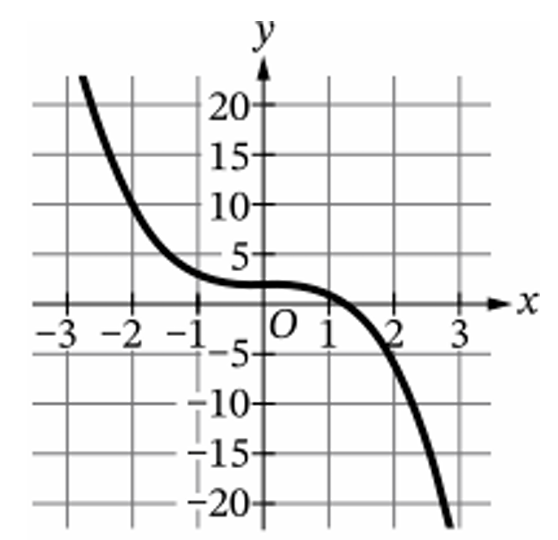
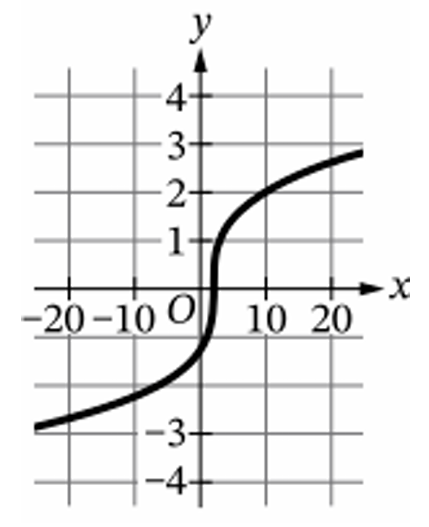
▶️ Answer/Explanation
The correct option is (D).
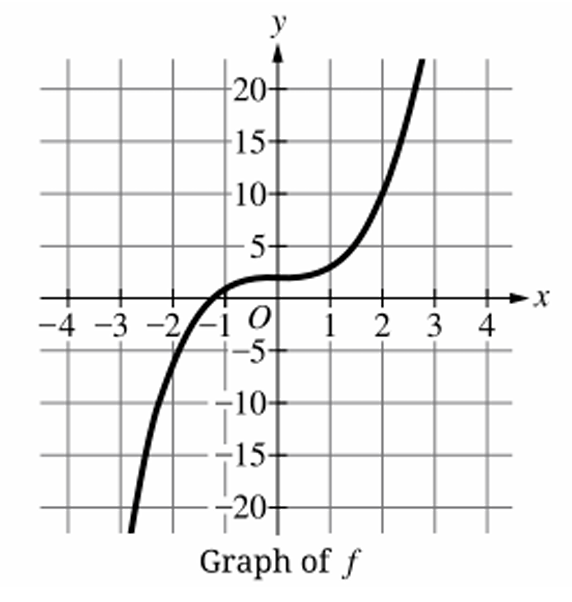
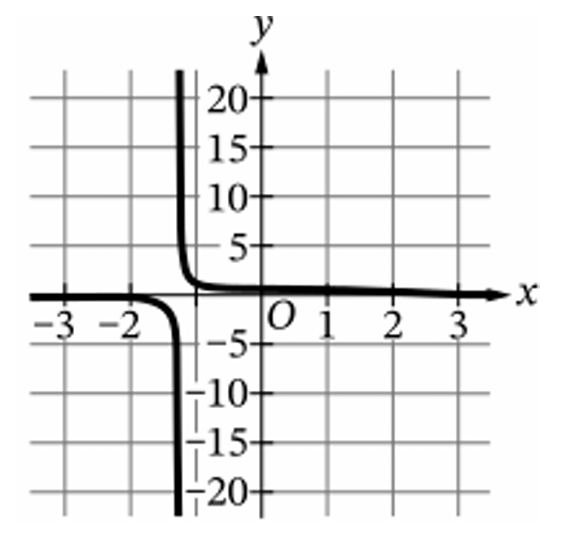
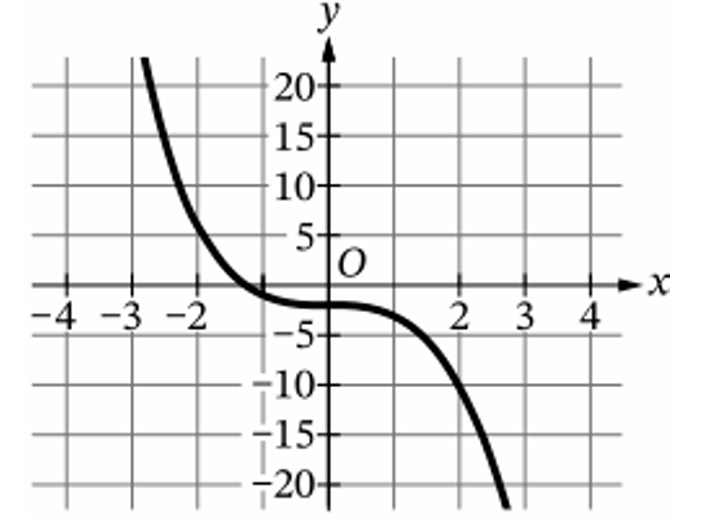
Identify key points on the graph of $y = f(x)$, such as $(-2, -10)$, $(0, 2)$, and $(2, 10)$.
For the inverse function $y = f^{-1}(x)$, the $x$ and $y$ coordinates are swapped.
The corresponding points on $f^{-1}(x)$ must be $(-10, -2)$, $(2, 0)$, and $(10, 2)$.
Graphically, $f^{-1}(x)$ is the reflection of $f(x)$ across the line $y = x$.
Option (D) is the only graph that contains these swapped points and reflects the original shape.
Notice the $x$-axis scale in (D) extends to $\pm 20$, matching the original $y$-axis range.
Question
(B) $\frac{5x+6}{4}$
(C) $\frac{5x}{4} – 6$
(D) $\frac{5x-6}{4}$
▶️ Answer/Explanation
Set the function $y = \frac{4x+6}{5}$.
Swap the variables $x$ and $y$ to get $x = \frac{4y+6}{5}$.
Multiply both sides by $5$ to obtain $5x = 4y + 6$.
Subtract $6$ from both sides: $5x – 6 = 4y$.
Divide by $4$ to solve for $y$: $y = \frac{5x-6}{4}$.
Therefore, $g^{-1}(x) = \frac{5x-6}{4}$, which matches option (D).
Question
▶️ Answer/Explanation
The original function $W$ maps time $t$ to the amount of water $w$.
The inverse function $W^{-1}$ maps the amount of water $w$ back to time $t$.
Since $W$ is a decreasing function, as $t$ increases, $w$ decreases.
For any monotonic function, the inverse function $W^{-1}$ shares the same monotonicity as the original function.
Therefore, $W^{-1}$ must also be a decreasing function.
As the input of $W^{-1}$ is the “amount of water,” the correct description is that it is a decreasing function of the amount of water.
Thus, the correct option is (D).
Question
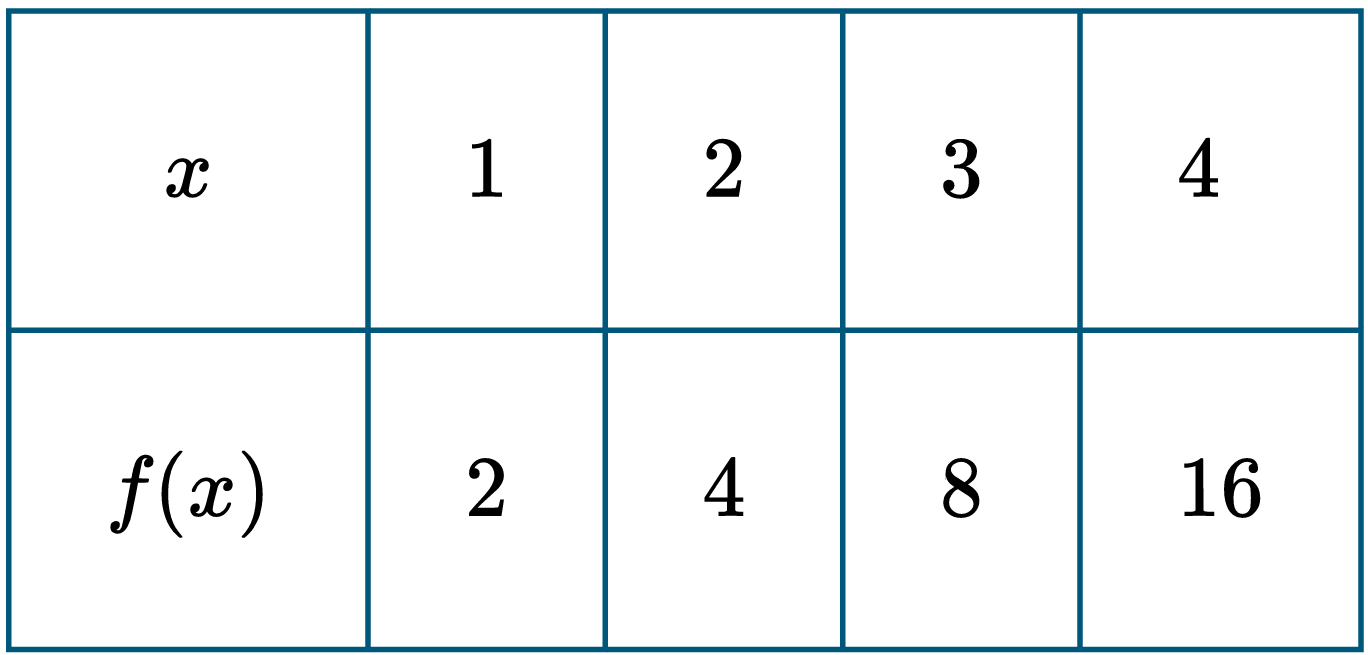
The table gives values of the function $f$ for selected values of $x$. Which of the following is a verbal representation of $f^{-1}(x)$, the inverse function of $f$?
▶️ Answer/Explanation
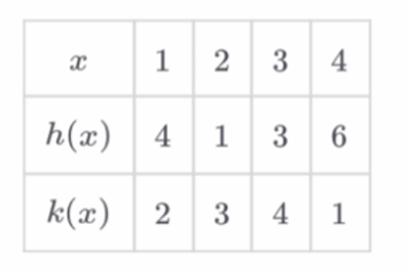
The original function $f$ is exponential because as $x$ increases by $1$, $f(x)$ doubles ($2, 4, 8, 16$).
The inverse of an exponential function is a logarithmic function, ruling out (C) and (D).
For the inverse function $f^{-1}(x)$, the inputs and outputs of $f$ are swapped.
The inputs of $f^{-1}(x)$ are the values $\{2, 4, 8, 16\}$ and the outputs are $\{1, 2, 3, 4\}$.
As the input values of $f^{-1}(x)$ double, the output values increase by $1$.
This matches the description provided in option (B).
Therefore, $f^{-1}(x)$ is logarithmic with output values increasing by $1$ every time input values double.
Question
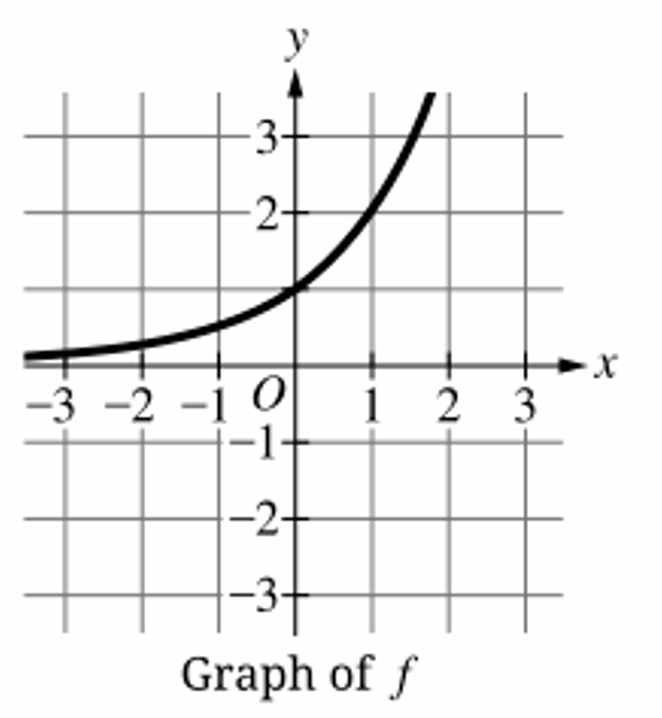
(A) 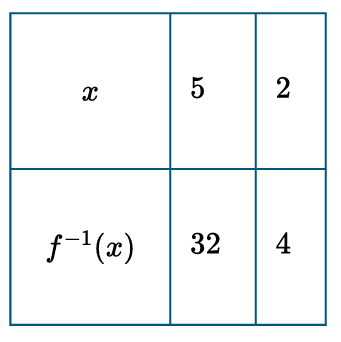
(B) 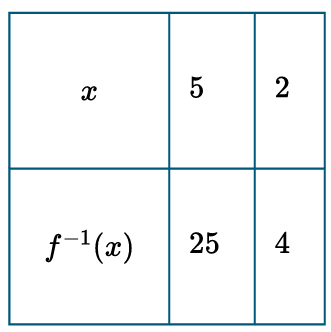
(C) 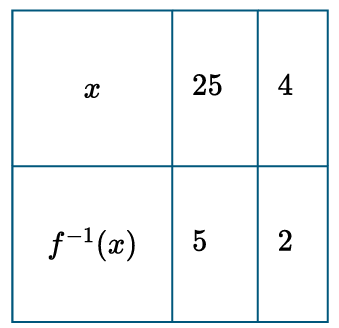
(D) 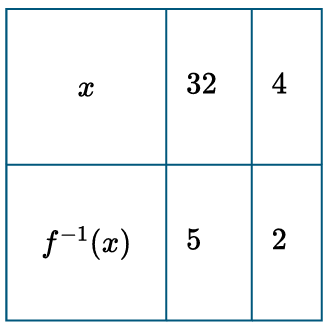
▶️ Answer/Explanation
The graph shows $f$ passes through $(0, 1)$, $(1, 2)$, and $(2, 4)$.
This indicates the exponential function is defined by $f(x) = 2^x$.
An inverse function $f^{-1}(x)$ swaps input and output: $(x, y) \rightarrow (y, x)$.
Since $f(2) = 4$, the inverse must contain the point $(4, 2)$.
Since $f(5) = 2^5 = 32$, the inverse must contain the point $(32, 5)$.
Table (D) is the only one correctly matching these coordinates.
Therefore, (D) is the correct table for the inverse function.
Question
▶️ Answer/Explanation
The initial population at $t = 0$ is $P_0 = 30,000$.
The growth rate is $2.3\%$, so the growth factor is $1 + 0.023 = 1.023$.
The population $p$ after $t$ years is given by $p = 30,000 \cdot (1.023)^t$.
To find years $t$ as a function of population $p$, we solve for $t$:
Divide both sides by $30,000$ to get $\frac{p}{30,000} = (1.023)^t$.
Convert the exponential equation to logarithmic form: $t = \log_{1.023} \left( \frac{p}{30,000} \right)$.
Therefore, the correct function is $g(p) = \log_{1.023} \left( \frac{p}{30,000} \right)$.
The correct option is (B).
Question
▶️ Answer/Explanation
The correct option is (A).
• The problem states that the point \( (3, -2) \) is on the graph of \( g \), which means \( g(3) = -2 \).
• We substitute \( x = 3 \) into the given equation \( h(x) = 2g(x) + 3 \) to find the corresponding point on \( h \).
• This gives \( h(3) = 2(-2) + 3 = -4 + 3 = -1 \).
• Thus, the point \( (3, -1) \) lies on the graph of the function \( h \).
• For an inverse function \( h^{-1} \), the input and output values are swapped; so if \( (a, b) \) is on \( h \), then \( (b, a) \) is on \( h^{-1} \).
• Swapping the coordinates of \( (3, -1) \) gives the point \( (-1, 3) \).
• Therefore, the point \( (-1, 3) \) is on the graph of \( h^{-1} \).
Question
▶️ Answer/Explanation
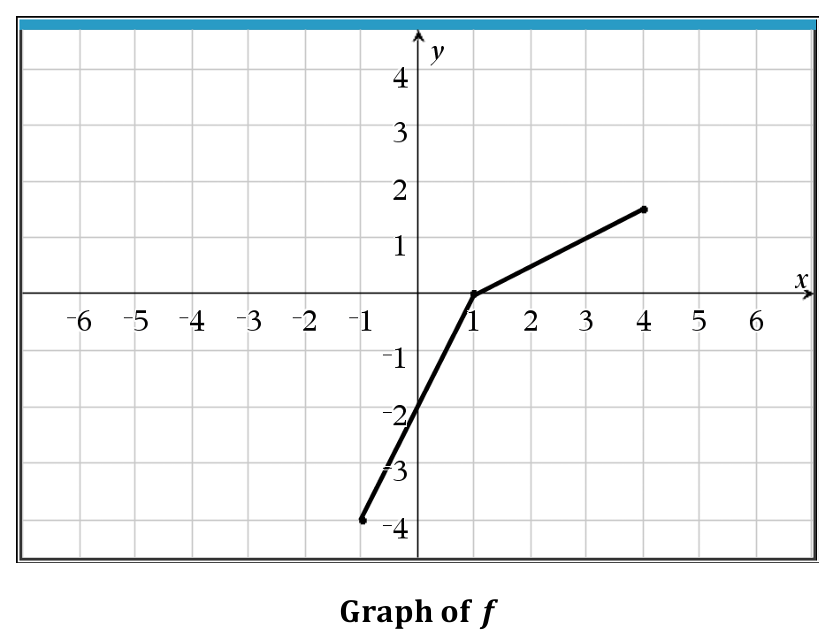
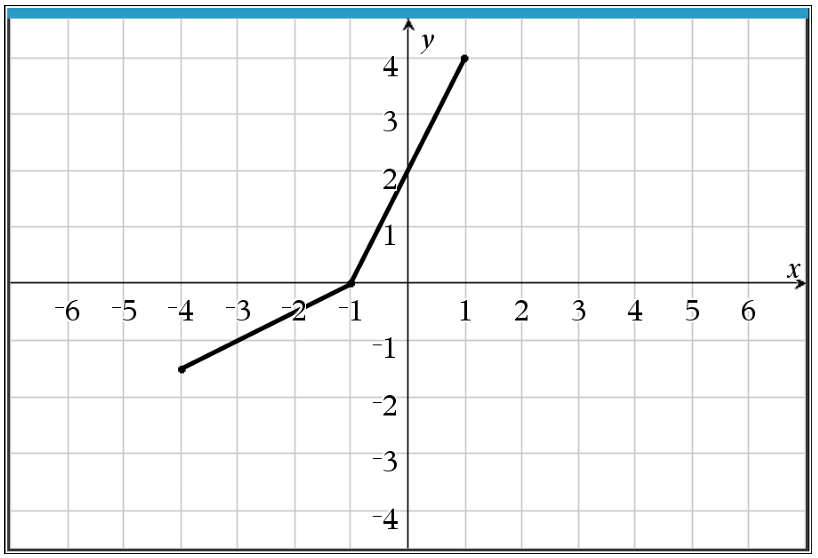
The graph of $f$ contains the key endpoints and vertices: $(-1, -4)$, $(1, 0)$, and $(4, 2)$.
For an inverse function $f^{-1}$, the coordinates $(x, y)$ of $f$ are swapped to $(y, x)$.
The corresponding points for $f^{-1}$ must be $(-4, -1)$, $(0, 1)$, and $(2, 4)$.
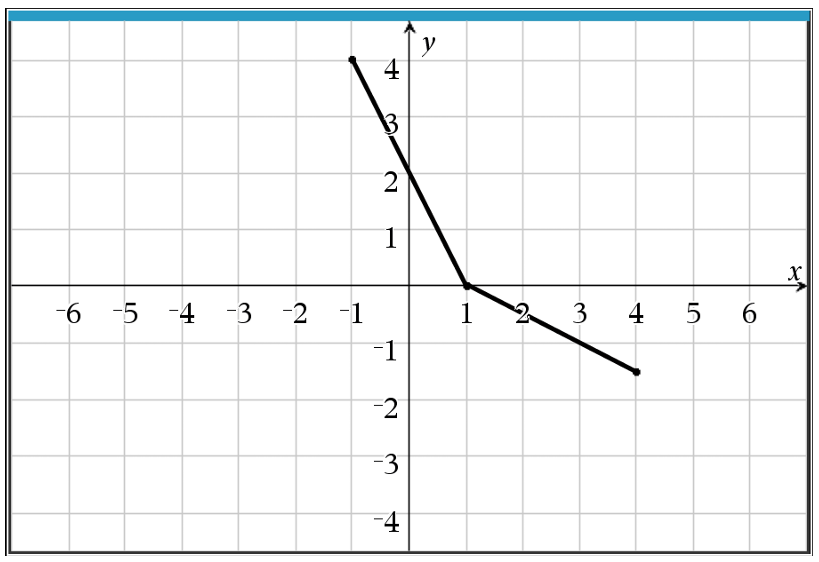
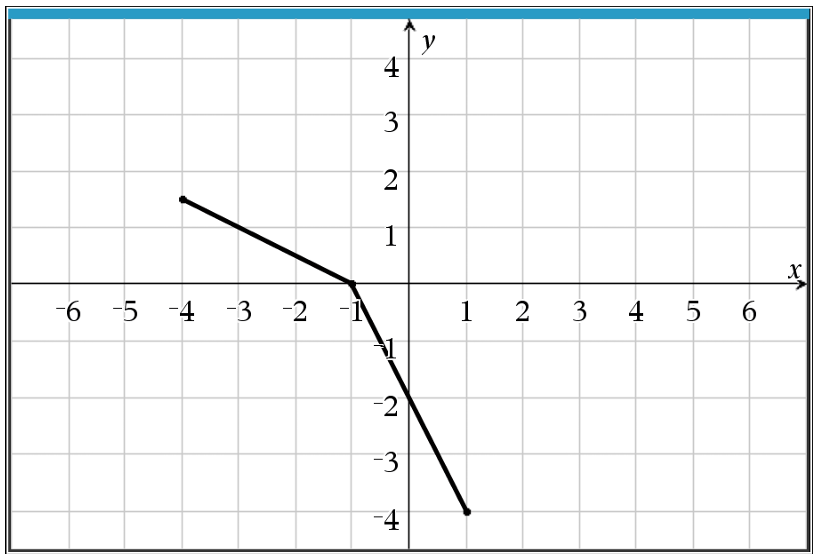
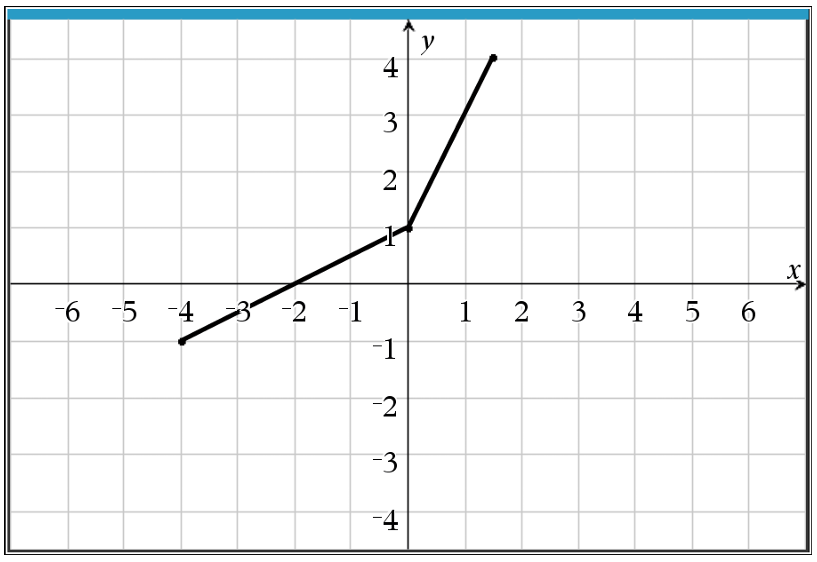
Graph (C) is the only option that contains these specific inverted coordinates.
Graphically, $f^{-1}$ is the reflection of $f$ across the line $y = x$.
Option (C) correctly reflects the two linear segments across the identity line $y = x$.
Question (Calc Allowed)
(B) $0$
(C) $1$
(D) $2$
▶️ Answer/Explanation
By definition of an inverse function, if $g$ is the inverse of $f$, then $g(y) = x$ is equivalent to $f(x) = y$.
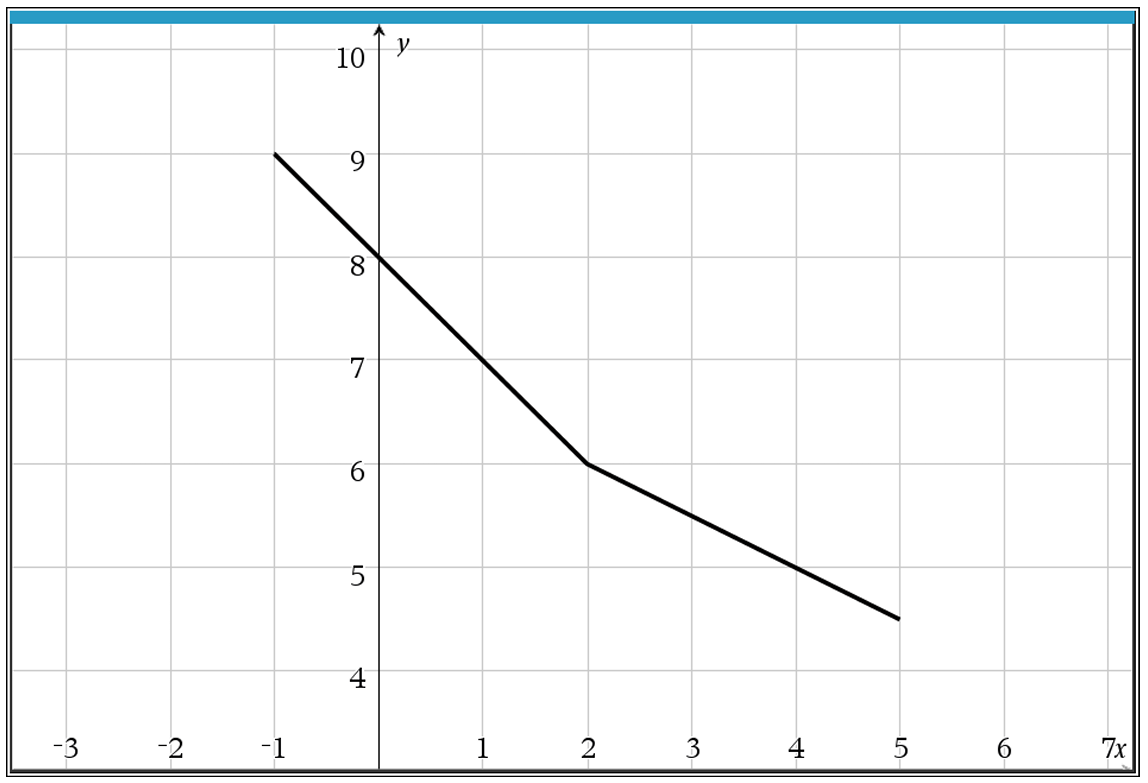
To find the value of $g(7)$, we must locate the point on the graph of $f$ where the $y$-coordinate is $7$.
Observing the provided graph, when $y = 7$, the corresponding $x$-coordinate on the line segment is $1$.
This means that $f(1) = 7$.
Therefore, $g(7) = 1$.
The correct option is (C).
Question
Most-appropriate topic codes (CED):
• TOPIC 1.10: Rational Functions and Holes — part (A)ii
• TOPIC 1.7: Rational Functions and End Behavior — part (B)i
• TOPIC 1.9: Rational Functions and Vertical Asymptotes — part (B)ii
• TOPIC 2.10: Logarithmic Function Context and Data Modeling — part (C)
▶️ Answer/Explanation
(A)
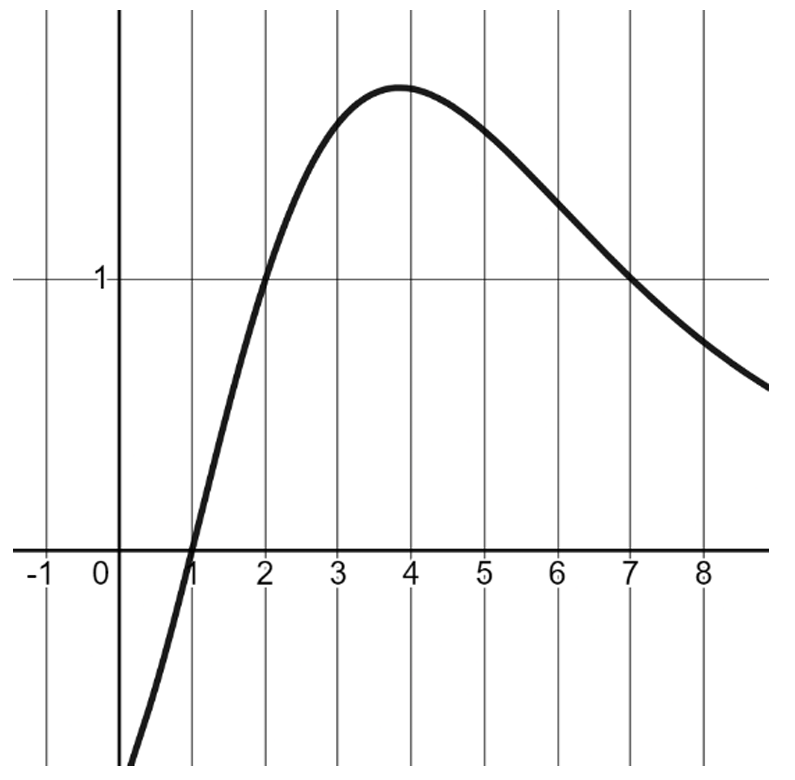
i. The graph of \( f(x) \) shows that \( f(2) \approx 1 \), so \( f^{-1}(1) \approx 2 \). From the table, \( g(2) = 1 \). Thus, \( g(f^{-1}(1)) \approx 1 \).
Since \( f(x) \) is continuous and increasing, the inverse is defined for values in its range.
The estimate is a single value, \( 1 \), as the graph aligns precisely with the point. No other values exist due to the strictly increasing nature of \( f(x) \).
ii. The graph of \( f(x) \) crosses zero at \( x=1 \), so \( f(1)=0 \), and from the table, \( g(1)=0 \).
Thus, \( h(1) \) is undefined (\( 0/0 \) form).
The limit as \( x \to 1 \) of \( h(x) \) exists and equals \( 1 \), since both \( g(x) \) and \( f(x) \) resemble \( \log_2(x) \), making \( h(x)=1 \) elsewhere.
This indicates a removable discontinuity at \( x=1 \). No other discontinuities for \( x>0 \), as \( f(x) \neq 0 \) elsewhere in the domain.
The location is \( x=1 \), type: removable.
(B)
i. As \( x \to \infty \), \( \ln(x) \to \infty \), so \( 4.99 – \ln(x) \to -\infty \), and \( \frac{1}{4.99 – \ln(x)} \to 0^- \).
The term \( e^{2 \sin(\sqrt{x})} \) oscillates between \( e^{-2} \) and \( e^{2} \), remaining bounded.
By the squeeze theorem, since the amplitude approaches \( 0 \), \( \lim_{x \to \infty} j(x) = 0 \).
The end behavior is that \( j(x) \) approaches \( 0 \). The limit exists.
ii. As \( x \to 0^+ \), \( \ln(x) \to -\infty \), so \( 4.99 – \ln(x) \to +\infty \), and \( \frac{1}{4.99 – \ln(x)} \to 0^+ \).
Also, \( \sqrt{x} \to 0^+ \), \( \sin(\sqrt{x}) \to 0^+ \), so \( e^{2 \sin(\sqrt{x})} \to e^0 = 1 \).
Thus, \( j(x) \to 0 \cdot 1 = 0 \).
The limit is \( \lim_{x \to 0^+} j(x) = 0 \).
No vertical asymptote at \( x=0 \), as the function approaches a finite value, not \( \pm \infty \).
(C)
The table shows \( g(x) \) values: at \( x=0.5, 1, 2, 4, 7, 8 \), \( g(x)=-1, 0, 1, 2, 2.807, 3 \).
When \( x \) doubles (\( 0.5 \) to \( 1 \), \( 1 \) to \( 2 \), \( 2 \) to \( 4 \), \( 4 \) to \( 8 \)), \( \Delta g = +1 \) consistently.
This pattern matches logarithmic functions, where outputs increase by a constant for multiplicative input changes.
Linear would require constant \( \Delta g \) for constant \( \Delta x \), but \( \Delta x \) varies while \( \Delta g =1 \) for doublings.
Quadratic would show constant second differences, but here first differences are not constant.
Exponential would show constant ratios in outputs for additive input changes, which does not fit.
Thus, best modeled by a logarithmic function like \( g(x) = \log_2(x) \).
Question
▶️ Answer/Explanation
Part A
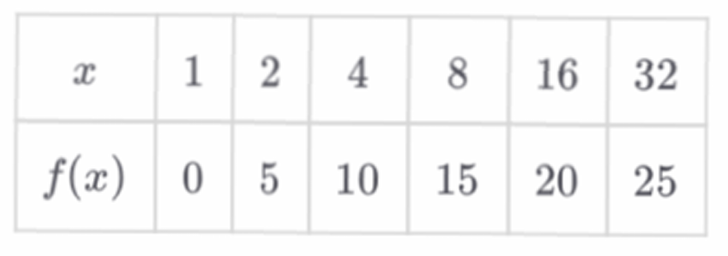
(i) From the table, we find $f(8) = 15$.
Substitute $15$ into the function $g(x)$: $h(8) = g(15) = 0.25(15)^3 – 9.5(15)^2 + 110(15) – 399$.
$h(8) = 0.25(3375) – 9.5(225) + 1650 – 399$.
$h(8) = 843.75 – 2137.5 + 1650 – 399$.
$h(8) = -42.75$.
(ii) To find $f^{-1}(20)$, we look for the $x$ value where $f(x) = 20$.
From the table, $f(16) = 20$.
Therefore, $f^{-1}(20) = 16$.
Part B
(i) We solve the equation $0.25x^3 – 9.5x^2 + 110x – 399 = -45$.
Set the equation to zero: $0.25x^3 – 9.5x^2 + 110x – 354 = 0$.
Using numerical methods or a graphing calculator, the real solutions are approximately:
$x \approx 5.242$
$x \approx 12.188$
$x \approx 20.570$
(ii) The end behavior of a polynomial is determined by its leading term, $0.25x^3$.
Since the leading coefficient is positive and the degree is odd, as $x \to \infty$, $g(x) \to \infty$.
The limit notation is $\lim_{x \to \infty} g(x) = \infty$.
Part C
(i) The function $f$ is best modeled by a logarithmic function.
(ii) In a logarithmic model, constant changes in the output values correspond to proportional changes in the input values.
As the output $f(x)$ increases by a constant $5$ ($0, 5, 10, 15 \dots$),
The input $x$ values are multiplied by a constant factor of $2$ ($1, 2, 4, 8 \dots$).
This constant ratio of inputs for constant additions of outputs is the hallmark of logarithmic growth.
Question
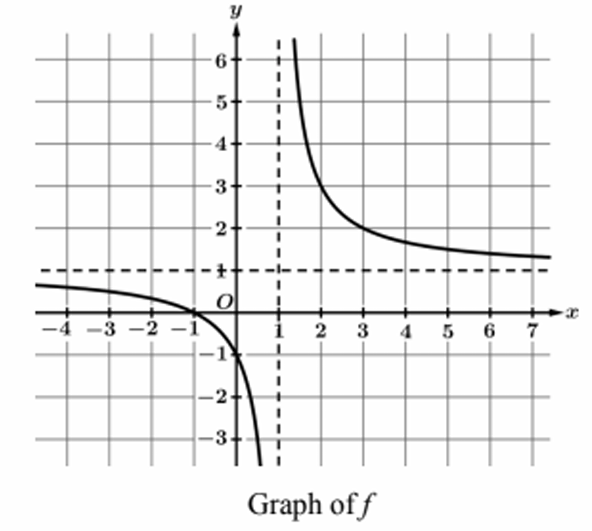
▶️ Answer/Explanation
(A)(i) Find \( h(3) \)
The function is defined as \( h(x) = g(f(x)) \).
First, we find the value of the inner function, \( f(3) \).
According to the problem text and graph, the point \( (3, 2) \) lies on the graph of \( f \). Therefore, \( f(3) = 2 \).
Now, substitute this value into the outer function \( g(x) \):
\( h(3) = g(2) \)
Using the definition \( g(x) = 2 + 3\ln x \):
\( g(2) = 2 + 3\ln(2) \)
Using a calculator to approximate \( \ln(2) \approx 0.693 \):
\( g(2) = 2 + 3(0.6931…) \approx 2 + 2.079 = 4.079 \)
Answer: \( h(3) \approx 4.079 \)
(A)(ii) Find real zeros of \( f \)
A real zero of a function occurs where the graph intersects the x-axis (where \( f(x) = 0 \)).
Looking at the provided graph, the curve intersects the x-axis at \( x = -1 \).
The problem text confirms the point \( (-1, 0) \) is on the graph.
There are no other intersections with the x-axis shown.
Answer: \( x = -1 \)
(B)(i) Find \( x \) for \( g(x) = e \)
Set up the equation:
\( 2 + 3\ln x = e \)
Subtract 2 from both sides:
\( 3\ln x = e – 2 \)
Divide by 3:
\( \ln x = \frac{e – 2}{3} \)
Convert from logarithmic to exponential form to solve for \( x \):
\( x = e^{\left(\frac{e – 2}{3}\right)} \)
Approximating the value (using \( e \approx 2.718 \)):
\( x \approx e^{0.2394} \)
Answer: \( x \approx 1.271 \)
(B)(ii) End behavior of \( g \)
We need to evaluate the limit as \( x \to \infty \) for \( g(x) = 2 + 3\ln x \).
As \( x \) increases without bound (\( x \to \infty \)), the natural logarithm function \( \ln x \) also increases without bound (\( \ln x \to \infty \)).
Multiplying by 3 and adding 2 does not change the unbounded nature.
Answer: \( \lim_{x \to \infty} g(x) = \infty \)
(C)(i) Is \( f \) invertible?
Answer: Yes, \( f \) is invertible.
(C)(ii) Reason
A function is invertible if and only if it is one-to-one. This can be verified visually using the Horizontal Line Test.
Looking at the graph of \( f(x) \):
1. The function is strictly decreasing on both branches of its domain (\( x < 1 \) and \( x > 1 \)).
2. The range of the left branch appears to be \( (-\infty, 1) \) and the range of the right branch appears to be \( (1, \infty) \).
Because the y-values do not repeat (no horizontal line intersects the graph more than once), the function is one-to-one.
Therefore, \( f \) has an inverse.
Question

▶️ Answer/Explanation
(A) (i)
First, evaluate the inner function \(f(5)\) using the table: \(f(5) = 34\).
Next, substitute this value into \(g(x)\) to find \(h(5) = g(34)\).
\(g(34) = \frac{34^3 – 14(34) – 27}{34 + 2}\)
\(g(34) = \frac{39304 – 476 – 27}{36} = \frac{38801}{36}\)
\(h(5) \approx 1077.806\)
(A) (ii)
To find \(f^{-1}(4)\), we look for the input value \(x\) in the table that produces an output of \(4\).
The table shows that \(f(3) = 4\).
Therefore, \(f^{-1}(4) = 3\).
(B) (i)
Set \(g(x) = 3\) and solve for \(x\):
\(\frac{x^3 – 14x – 27}{x + 2} = 3\)
Multiply both sides by \((x+2)\): \(x^3 – 14x – 27 = 3(x + 2)\)
Simplify: \(x^3 – 14x – 27 = 3x + 6\)
Rearrange into polynomial form: \(x^3 – 17x – 33 = 0\)
Using a graphing calculator to find the zero of this polynomial:
\(x \approx 4.879\)
(B) (ii)
We evaluate the limit as \(x \to -\infty\) for \(g(x)\).
\(\lim_{x \to -\infty} \frac{x^3 – 14x – 27}{x + 2}\)
By examining the leading terms, the function behaves like \(\frac{x^3}{x} = x^2\) for large absolute values of \(x\).
As \(x \to -\infty\), \(x^2 \to \infty\).
\(\lim_{x \to -\infty} g(x) = \infty\)
(C) (i)
Calculate the first differences of \(f(x)\): \((-5) – (-10) = 5\), \(4 – (-5) = 9\), \(17 – 4 = 13\), \(34 – 17 = 17\).
Calculate the second differences: \(9 – 5 = 4\), \(13 – 9 = 4\), \(17 – 13 = 4\).
Since the second differences are constant, \(f\) is best modeled by a quadratic function.
(C) (ii)
The model is quadratic because for equal intervals of the input values \(x\) (step size of \(1\)), the rate of change of the output values increases by a constant amount (constant second difference of \(4\)).