AP Precalculus -2.8 Inverse Functions- Study Notes - Effective Fall 2023
AP Precalculus -2.8 Inverse Functions- Study Notes – Effective Fall 2023
AP Precalculus -2.8 Inverse Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine the input-output pairs of the inverse of a function.
Determine the inverse of a function on an invertible domain.
Key Concepts:
Invertible Functions and Domain Restrictions
Inverse Functions as Reverse Mappings
Composition of a Function and Its Inverse
Domain and Range of Inverse Functions
Graphical Interpretation of Inverse Functions
Finding an Inverse Function Algebraically
Contextual Restrictions on Inverse Functions
Invertible Functions and Domain Restrictions
On a specified domain, a function \( \mathrm{f} \) has an inverse function, or is said to be invertible, if each output value of \( \mathrm{f} \) corresponds to exactly one input value.
In other words, an invertible function is a one-to-one function on its domain.![]()
This condition ensures that the inverse relation is also a function.
If a function is not one-to-one over its entire domain, its domain can often be restricted so that the function becomes invertible.
A domain restriction limits the set of input values so that no two different inputs produce the same output.
Key Idea
• Invertible functions have unique inputs for each output
• Domain restrictions are often used to ensure one-to-one behavior
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Explain why \( \mathrm{f} \) is not invertible on its full domain and describe a restriction that makes it invertible.
▶️ Answer/Explanation
On the full domain, different inputs produce the same output:
\( \mathrm{ \displaystyle f(2) = 4 \quad \text{and} \quad f(-2) = 4 } \)
Because the output 4 comes from two inputs, the function is not one-to-one.
Restricting the domain to \( \mathrm{x \ge 0} \) ensures that each output corresponds to a unique input.
Conclusion
With the restriction \( \mathrm{x \ge 0} \), the function becomes invertible.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = x^3 } \)
Determine whether \( \mathrm{f} \) is invertible on its full domain.
▶️ Answer/Explanation
The function \( \mathrm{f(x)=x^3} \) is strictly increasing for all real values of \( \mathrm{x} \).
Each output corresponds to exactly one input.
Conclusion
The function is invertible on its entire domain.
Inverse Functions as Reverse Mappings
An inverse function can be thought of as a reverse mapping of a function.
If a function \( \mathrm{f} \) is invertible on a specified domain, then its inverse function, denoted \( \mathrm{f^{-1}} \), maps the output values of \( \mathrm{f} \) back to their corresponding input values.
Symbolically, this means:
![]()
\( \mathrm{ \displaystyle \text{If } f(a) = b,\; \text{then } f^{-1}(b) = a } \)
Equivalently, if a function \( \mathrm{f} \) consists of ordered pairs \( \mathrm{(a,b)} \), then the inverse function consists of the ordered pairs \( \mathrm{(b,a)} \).
Thus, an inverse function interchanges the roles of input and output.
Key Properties
![]()
• The domain of \( \mathrm{f^{-1}} \) is the range of \( \mathrm{f} \)
• The range of \( \mathrm{f^{-1}} \) is the domain of \( \mathrm{f} \)
• Inverse functions exist only when \( \mathrm{f} \) is one-to-one on its domain
Example
The function \( \mathrm{f} \) contains the ordered pairs
\( \mathrm{ (1,4),\; (2,7),\; (3,10) } \)
Write the ordered pairs of the inverse function.
▶️ Answer/Explanation
Swap each input-output pair:
\( \mathrm{ (4,1),\; (7,2),\; (10,3) } \)
Conclusion
The inverse function maps outputs of \( \mathrm{f} \) back to their original inputs.
Example
Let
\( \mathrm{ \displaystyle f(x) = 3x – 5 } \)
Given that \( \mathrm{f(4) = 7} \), interpret \( \mathrm{f^{-1}(7)} \).
▶️ Answer/Explanation
Since \( \mathrm{f(4) = 7} \), the inverse reverses this mapping.
\( \mathrm{ \displaystyle f^{-1}(7) = 4 } \)
Conclusion
The inverse function maps the output value 7 back to the input value 4.
Composition of a Function and Its Inverse
If a function \( \mathrm{f} \) is invertible on a specified domain, then composing the function with its inverse results in the identity function.
This means that applying a function and then applying its inverse (or vice versa) returns the original input value.![]()
Mathematically, this relationship is expressed as
\( \mathrm{ \displaystyle f\!\left(f^{-1}(x)\right) = x } \)
and
\( \mathrm{ \displaystyle f^{-1}\!\left(f(x)\right) = x } \)
These equalities hold for all values of \( \mathrm{x} \) in the appropriate domains.
This property shows that inverse functions undo each other, just as subtraction undoes addition and division undoes multiplication.
Example
Let
\( \mathrm{ \displaystyle f(x) = 3x + 2 } \)
The inverse of \( \mathrm{f} \) is
\( \mathrm{ \displaystyle f^{-1}(x) = \dfrac{x – 2}{3} } \)
Verify that composing \( \mathrm{f} \) and \( \mathrm{f^{-1}} \) gives the identity function.
▶️ Answer/Explanation
Compute \( \mathrm{f\!\left(f^{-1}(x)\right)} \):
\( \mathrm{ \displaystyle f\!\left(\dfrac{x – 2}{3}\right) = 3\!\left(\dfrac{x – 2}{3}\right) + 2 = x } \)
Compute \( \mathrm{f^{-1}\!\left(f(x)\right)} \):
\( \mathrm{ \displaystyle f^{-1}(3x + 2) = \dfrac{(3x + 2) – 2}{3} = x } \)
Conclusion
Both compositions return \( \mathrm{x} \), confirming the identity function.
Example
Let
\( \mathrm{ \displaystyle f(x) = x^3 } \)
The inverse of \( \mathrm{f} \) is
\( \mathrm{ \displaystyle f^{-1}(x) = \sqrt[3]{x} } \)
Verify the identity property.
▶️ Answer/Explanation
\( \mathrm{ \displaystyle f\!\left(f^{-1}(x)\right) = \left(\sqrt[3]{x}\right)^3 = x } \)
\( \mathrm{ \displaystyle f^{-1}\!\left(f(x)\right) = \sqrt[3]{x^3} = x } \)
Conclusion
A function and its inverse always compose to the identity function on their valid domains.
Domain and Range of Inverse Functions
On a function’s invertible domain, the domain and range of a function are interchanged when forming its inverse.
![]()
Specifically:
• The domain of \( \mathrm{f^{-1}} \) is the range of \( \mathrm{f} \)
• The range of \( \mathrm{f^{-1}} \) is the domain of \( \mathrm{f} \)
This reversal occurs because an inverse function undoes the original mapping by swapping inputs and outputs.
When a function is represented by a table of values, the inverse function can be found by reversing each ordered pair.
That is, if the original function contains the pair
\( \mathrm{ \displaystyle (a,b) } \)
then the inverse function contains the pair
\( \mathrm{ \displaystyle (b,a) } \)
This method works only when the function is one-to-one, ensuring the inverse is also a function.
Example
A function is represented by the table:
\( \mathrm{ (1,3),\; (2,5),\; (4,9) } \)
Find the table of values for the inverse function and identify its domain and range.
▶️ Answer/Explanation
Reverse each ordered pair:
\( \mathrm{ (3,1),\; (5,2),\; (9,4) } \)
Domain and Range
Domain of \( \mathrm{f} \): \( \mathrm{\{1,2,4\}} \)
Range of \( \mathrm{f} \): \( \mathrm{\{3,5,9\}} \)
Domain of \( \mathrm{f^{-1}} \): \( \mathrm{\{3,5,9\}} \)
Range of \( \mathrm{f^{-1}} \): \( \mathrm{\{1,2,4\}} \)
Example
The function \( \mathrm{f} \) has domain \( \mathrm{x \ge 0} \) and is defined by
\( \mathrm{ \displaystyle f(x) = \sqrt{x} } \)
State the domain and range of the inverse function.
▶️ Answer/Explanation
The range of \( \mathrm{f} \) is \( \mathrm{y \ge 0} \).
The inverse function is
\( \mathrm{ \displaystyle f^{-1}(x) = x^2 } \)
Conclusion
Domain of \( \mathrm{f^{-1}} \): \( \mathrm{x \ge 0} \)
Range of \( \mathrm{f^{-1}} \): \( \mathrm{y \ge 0} \)
Graphical Interpretation of Inverse Functions
The inverse of the graph of a function \( \mathrm{y=f(x)} \) can be obtained by reversing the roles of the \( \mathrm{x} \)- and \( \mathrm{y} \)-axes.
Graphically, this is accomplished by reflecting the graph of the function across the line![]()
\( \mathrm{ \displaystyle y = x } \)
The line \( \mathrm{y=x} \) is the graph of the identity function and acts as a mirror line for a function and its inverse.
If a point \( \mathrm{(a,b)} \) lies on the graph of \( \mathrm{y=f(x)} \), then the point \( \mathrm{(b,a)} \) lies on the graph of the inverse function \( \mathrm{y=f^{-1}(x)} \).
Key Observations
• A function and its inverse are mirror images across \( \mathrm{y=x} \)
• The x-intercepts of \( \mathrm{f} \) become y-intercepts of \( \mathrm{f^{-1}} \)
• The domain and range are exchanged
Example
The graph of a function \( \mathrm{f} \) includes the points
\( \mathrm{ (1,4),\; (2,6),\; (5,10) } \)
Determine points on the graph of \( \mathrm{f^{-1}} \).
▶️ Answer/Explanation
Swap the coordinates of each point:
\( \mathrm{ (4,1),\; (6,2),\; (10,5) } \)
Conclusion
These points lie on the graph of the inverse function, which is the reflection of the original graph across \( \mathrm{y=x} \).
Example
Consider the function
\( \mathrm{ \displaystyle y = 2x + 1 } \)
Describe how the graph of its inverse is related to the graph of the original function.
▶️ Answer/Explanation
Solve for the inverse:
\( \mathrm{ \displaystyle x = 2y + 1 \Rightarrow y = \dfrac{x – 1}{2} } \)
The graph of \( \mathrm{y=\dfrac{x-1}{2}} \) is the reflection of \( \mathrm{y=2x+1} \) across the line \( \mathrm{y=x} \).
Conclusion
Every point on the original line corresponds to a reflected point on the inverse line.
Finding an Inverse Function Algebraically
An inverse function can be found by determining the inverse operations that reverse the original mapping of a function.
A standard algebraic method for finding the inverse of a function \( \mathrm{f} \) is based on the idea that the inverse reverses the roles of input and output.
Procedure
• Start with the equation \( \mathrm{y=f(x)} \)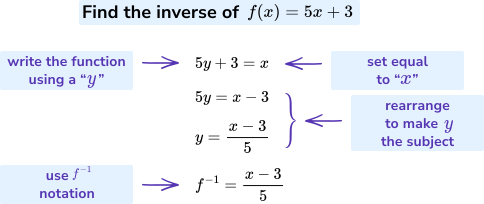
• Interchange \( \mathrm{x} \) and \( \mathrm{y} \)
• Solve the new equation for \( \mathrm{y} \)
• The resulting expression is \( \mathrm{y=f^{-1}(x)} \)
This process works only when the original function is invertible on its specified domain.
Example
Find the inverse of the function
\( \mathrm{ \displaystyle f(x) = 4x – 7 } \)
▶️ Answer/Explanation
Write the equation:
\( \mathrm{ \displaystyle y = 4x – 7 } \)
Swap \( \mathrm{x} \) and \( \mathrm{y} \):
\( \mathrm{ \displaystyle x = 4y – 7 } \)
Solve for \( \mathrm{y} \):
\( \mathrm{ \displaystyle x + 7 = 4y } \)
\( \mathrm{ \displaystyle y = \dfrac{x + 7}{4} } \)
Conclusion
The inverse function is \( \mathrm{f^{-1}(x)=\dfrac{x+7}{4}} \).
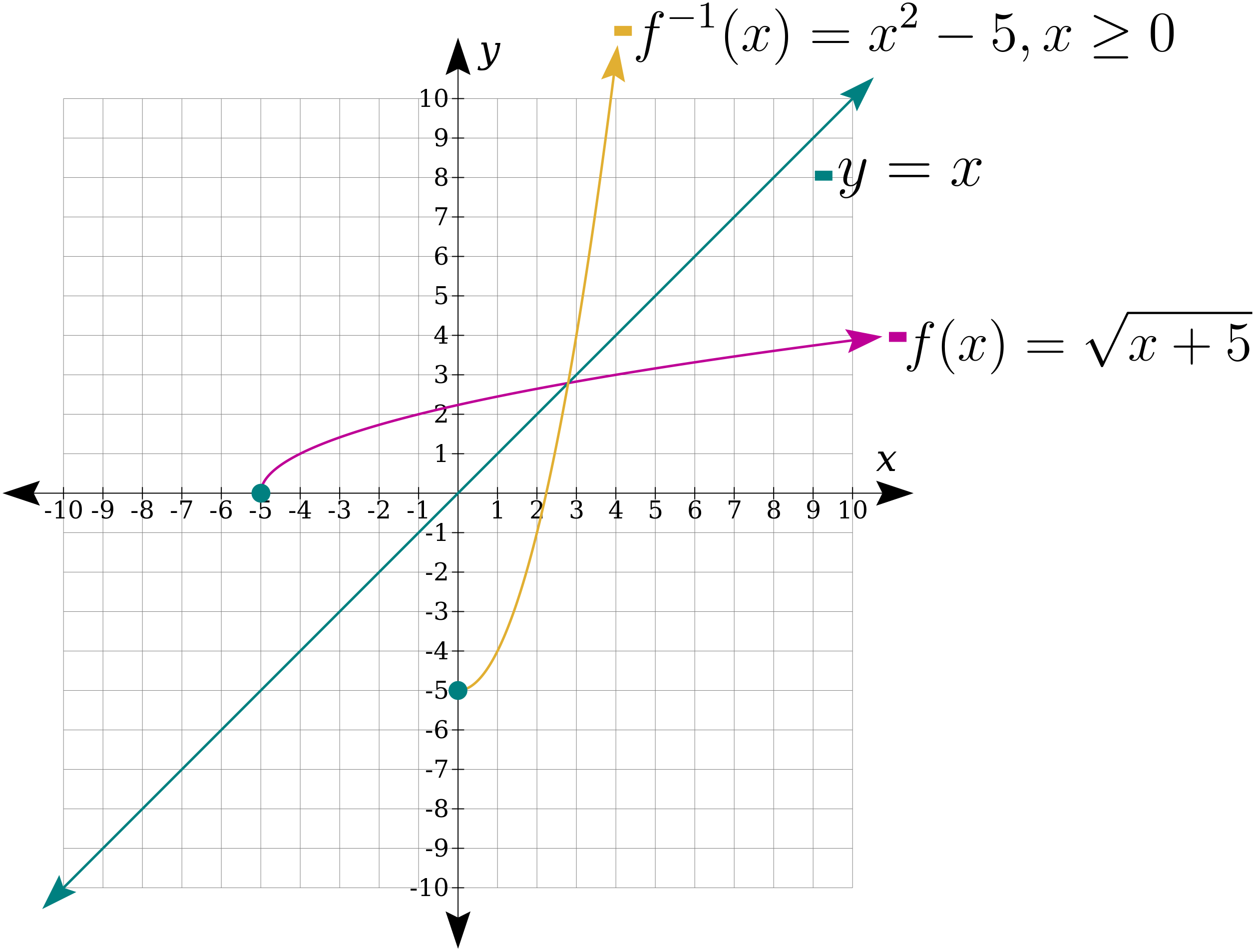
Example
Find the inverse of the function
\( \mathrm{ \displaystyle f(x) = \sqrt{x – 3} } \)
Assume the domain is \( \mathrm{x \ge 3} \).
▶️ Answer/Explanation
Start with the equation:
\( \mathrm{ \displaystyle y = \sqrt{x – 3} } \)
Swap \( \mathrm{x} \) and \( \mathrm{y} \):
\( \mathrm{ \displaystyle x = \sqrt{y – 3} } \)
Solve for \( \mathrm{y} \):
\( \mathrm{ \displaystyle x^2 = y – 3 } \)
\( \mathrm{ \displaystyle y = x^2 + 3 } \)
Conclusion
The inverse function is \( \mathrm{f^{-1}(x)=x^2+3} \), with domain \( \mathrm{x \ge 0} \).
Contextual Restrictions on Inverse Functions
In addition to limiting the domain of a function to make it invertible, contextual restrictions may also limit when an inverse function is meaningful or applicable.
Even if a function is mathematically invertible, the real-world situation being modeled may restrict the values that make sense for inputs or outputs.
Because the domain of the inverse function is the range of the original function, any contextual limitations on outputs of the original function directly affect the allowable inputs of the inverse.
Key Idea
• Mathematical invertibility does not guarantee contextual validity
• Context may restrict the inverse to a smaller domain than algebra alone suggests
Example
A company models the cost of producing items by the function
\( \mathrm{ \displaystyle C(x) = 50 + 10x } \)
where \( \mathrm{x} \) is the number of items produced and \( \mathrm{C(x)} \) is the cost in dollars.
Explain how context restricts the inverse function.
▶️ Answer/Explanation
Algebraically, the inverse is
\( \mathrm{ \displaystyle C^{-1}(x) = \dfrac{x – 50}{10} } \)
However, the number of items produced cannot be negative.
This means the inverse function is only valid for
\( \mathrm{ \displaystyle x \ge 50 } \)
Conclusion
Although the inverse exists algebraically for all real values, context restricts it to costs of at least \$50.
Example
The height of a ball (in meters) thrown upward is modeled by
\( \mathrm{ \displaystyle h(t) = -5t^2 + 20t } \)
where \( \mathrm{t} \) is time in seconds.
Explain why context limits the applicability of the inverse.
▶️ Answer/Explanation
The ball reaches the same height at two different times: once while rising and once while falling.
To form an inverse, the domain must be restricted to either the rising portion or the falling portion of the motion.
Additionally, time cannot be negative, and height cannot be negative in this context.
Conclusion
Even after restricting the domain mathematically, real-world constraints further limit when the inverse function is meaningful.
