AP Precalculus -2.9 Logarithmic Expressions- Study Notes - Effective Fall 2023
AP Precalculus -2.9 Logarithmic Expressions- Study Notes – Effective Fall 2023
AP Precalculus -2.9 Logarithmic Expressions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Evaluate logarithmic expressions.
Key Concepts:
Logarithmic Expressions
Evaluating Logarithmic Expressions
Logarithmic Scales and Multiplicative Change
Logarithmic Expressions
A logarithmic expression represents the exponent to which a base must be raised in order to produce a given value.
Specifically, the expression
\( \mathrm{ \displaystyle \log_b c = a } \)
means that
\( \mathrm{ \displaystyle b^a = c } \)
These two statements are equivalent and describe the same relationship.
Conditions
• \( \mathrm{b > 0} \)
• \( \mathrm{b \ne 1} \)
• \( \mathrm{c > 0} \)
When the base of a logarithm is not written, it is understood to be the common logarithm with base 10:
\( \mathrm{ \displaystyle \log c = \log_{10} c } \)
Logarithms are the inverse operations of exponential functions.
Example
Evaluate the logarithmic expression
\( \mathrm{ \displaystyle \log_2 8 } \)
▶️ Answer/Explanation
Rewrite the logarithm as an exponential equation:
\( \mathrm{ \displaystyle 2^a = 8 } \)
Since \( \mathrm{2^3 = 8} \), the value of the logarithm is
\( \mathrm{ \displaystyle \log_2 8 = 3 } \)
Example
Interpret the common logarithm
\( \mathrm{ \displaystyle \log 1000 } \)
▶️ Answer/Explanation
Since no base is written, the base is 10.
Rewrite as an exponential equation:
\( \mathrm{ \displaystyle 10^a = 1000 } \)
Because \( \mathrm{10^3 = 1000} \),
\( \mathrm{ \displaystyle \log 1000 = 3 } \)
Conclusion
The logarithm gives the exponent needed to obtain 1000 from the base 10.
Evaluating Logarithmic Expressions
Some logarithmic expression values can be found exactly using basic arithmetic, while others cannot be expressed simply and must be estimated using technology.

Exact values are typically available when the argument of the logarithm is a power of the base.
When the argument is not an exact power of the base, the logarithmic value is usually an irrational number and is therefore estimated using calculators or software.
Key Idea
• Exact values come from recognizing powers
• Approximations are used when exact powers are not present
Example
Evaluate the logarithmic expression
\( \mathrm{ \displaystyle \log_5 125 } \)
▶️ Answer/Explanation
Rewrite as an exponential equation:
\( \mathrm{ \displaystyle 5^a = 125 } \)
Since \( \mathrm{5^3 = 125} \),
\( \mathrm{ \displaystyle \log_5 125 = 3 } \)
Example
Estimate the value of
\( \mathrm{ \displaystyle \log_{10} 7 } \)
▶️ Answer/Explanation
The number 7 is not a power of 10.
Using technology,
\( \mathrm{ \displaystyle \log_{10} 7 \approx 0.845 } \)
Conclusion
Technology allows us to approximate logarithmic values that cannot be found exactly.
Logarithmic Scales and Multiplicative Change
On a logarithmic scale, equal spacing on the scale represents a multiplicative change rather than an additive change.
Each unit increase on a logarithmic scale corresponds to multiplying by the base of the logarithm.
For comparison:
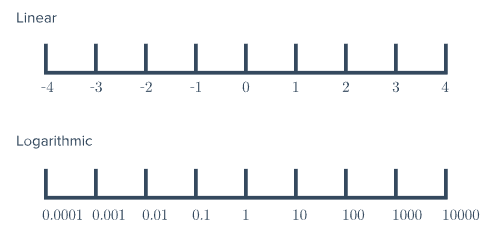
• On a standard (linear) scale, units increase additively, such as \( \mathrm{0,1,2,3,\ldots} \)
• On a logarithmic scale with base 10, units increase multiplicatively, such as \( \mathrm{10^0,10^1,10^2,10^3,\ldots} \)
This means that each step to the right on a base-10 logarithmic scale represents a value that is 10 times larger than the previous value.
Logarithmic scales are especially useful for representing data that span many orders of magnitude, such as sound intensity, earthquake magnitude, and population growth.
Example
A graph uses a logarithmic scale with base 10 on the horizontal axis.
If one point is at \( \mathrm{10^2} \) and another is one unit to the right, find the value represented by the second point.
▶️ Answer/Explanation
Each unit increase represents multiplication by 10.
\( \mathrm{ \displaystyle 10^2 \times 10 = 10^3 } \)
Conclusion
The second point represents the value \( \mathrm{10^3} \).
Example
Two values on a base-10 logarithmic scale are separated by 3 units.
Determine how many times larger the greater value is compared to the smaller value.
▶️ Answer/Explanation
Each unit corresponds to a factor of 10.
\( \mathrm{ \displaystyle 10^3 = 1000 } \)
Conclusion
The larger value is 1000 times greater than the smaller value.
