AP Precalculus -3.11 Secant, Cosecant, and Cotangent- Study Notes - Effective Fall 2023
AP Precalculus -3.11 Secant, Cosecant, and Cotangent- Study Notes – Effective Fall 2023
AP Precalculus -3.11 Secant, Cosecant, and Cotangent- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify key characteristics of functions that involve quotients of the sine and cosine functions.
Key Concepts:
The Secant Function
The Cosecant Function
Graphs of the Secant and Cosecant Functions
The Cotangent Function
Graphical Behavior of the Cotangent Function
The Secant Function
The secant function is defined as the reciprocal of the cosine function.
\( f(\theta) = \sec \theta = \dfrac{1}{\cos \theta} \)![]()
The secant function is defined only when the cosine function is not zero.
\( \cos \theta \ne 0 \)
Since \( \cos \theta = 0 \) at angles of the form
\( \theta = \dfrac{\pi}{2} + k\pi \), where \( k \) is an integer,
the secant function is undefined at these values and has vertical asymptotes there.
Because secant is the reciprocal of cosine, it has the same period as cosine, which is
\( 2\pi \).
The range of the secant function is
\( (-\infty, -1] \cup [1, \infty) \).
Example:
Evaluate \( \sec\!\left(\dfrac{\pi}{3}\right) \).
▶️ Answer/Explanation
First, find the cosine value:
\( \cos\!\left(\dfrac{\pi}{3}\right) = \dfrac{1}{2} \)
Now take the reciprocal:
\( \sec\!\left(\dfrac{\pi}{3}\right) = \dfrac{1}{\frac{1}{2}} = 2 \)
Final answer: \( \sec\!\left(\dfrac{\pi}{3}\right) = 2 \).
Example:
Determine where the function \( y = \sec \theta \) is undefined.
▶️ Answer/Explanation
The secant function is undefined when the cosine is zero.
This occurs at
\( \theta = \dfrac{\pi}{2} + k\pi \), where \( k \) is any integer.
Conclusion: \( y = \sec \theta \) is undefined at these values and has vertical asymptotes there.
The Cosecant Function
The cosecant function is defined as the reciprocal of the sine function.
\( f(\theta) = \csc \theta = \dfrac{1}{\sin \theta} \)![]()
The cosecant function is defined only when the sine function is not zero.
\( \sin \theta \ne 0 \)
Since \( \sin \theta = 0 \) at angles of the form
\( \theta = k\pi \), where \( k \) is an integer,
the cosecant function is undefined at these values and has vertical asymptotes there.
Because cosecant is the reciprocal of sine, it has the same period as sine, which is
\( 2\pi \).
The range of the cosecant function is
\( (-\infty, -1] \cup [1, \infty) \).
Example:
Evaluate \( \csc\!\left(\dfrac{\pi}{2}\right) \).
▶️ Answer/Explanation
First, evaluate the sine:
\( \sin\!\left(\dfrac{\pi}{2}\right) = 1 \)
Now take the reciprocal:
\( \csc\!\left(\dfrac{\pi}{2}\right) = \dfrac{1}{1} = 1 \)
Final answer: \( \csc\!\left(\dfrac{\pi}{2}\right) = 1 \).
Example:
Determine where the function \( y = \csc \theta \) is undefined.
▶️ Answer/Explanation
The cosecant function is undefined when the sine function equals zero.
This occurs at
\( \theta = k\pi \), where \( k \) is any integer.
Conclusion: \( y = \csc \theta \) has vertical asymptotes at these values.
Graphs of the Secant and Cosecant Functions
The secant and cosecant functions are reciprocal trigonometric functions, so their graphs reflect the behavior of the cosine and sine functions.
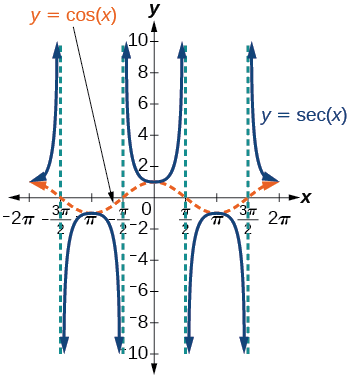
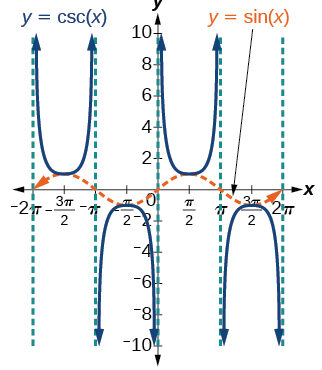
Vertical Asymptotes
The graph of the secant function, \( y = \sec \theta \), has vertical asymptotes at values of \( \theta \) where the cosine function is zero.
\( \cos \theta = 0 \Rightarrow \theta = \dfrac{\pi}{2} + k\pi \)
The graph of the cosecant function, \( y = \csc \theta \), has vertical asymptotes at values of \( \theta \) where the sine function is zero.
\( \sin \theta = 0 \Rightarrow \theta = k\pi \)
where \( k \) is any integer.
Range
Because secant and cosecant are reciprocals of cosine and sine, their output values cannot lie between −1 and 1.
Range: \( (-\infty, -1] \cup [1, \infty) \)
This means the graphs consist of branches that lie entirely above \( y = 1 \) or below \( y = -1 \).
Example:
State the vertical asymptotes and range of the function \( y = \sec \theta \).
▶️ Answer/Explanation
Vertical asymptotes
\( \theta = \dfrac{\pi}{2} + k\pi \)
Range
\( (-\infty, -1] \cup [1, \infty) \)
Example:
Explain why the range of \( y = \csc \theta \) does not include values between −1 and 1.
▶️ Answer/Explanation
The sine function has values between −1 and 1.
Taking the reciprocal of any value in this interval produces a value with magnitude greater than or equal to 1.
Therefore, the range excludes values between −1 and 1.
The Cotangent Function
The cotangent function is defined as the reciprocal of the tangent function.
\( f(\theta) = \cot \theta = \dfrac{1}{\tan \theta} \)
Because the tangent function is undefined when \( \cos \theta = 0 \), the cotangent function can also be written in terms of sine and cosine as
\( \cot \theta = \dfrac{\cos \theta}{\sin \theta} \)![]()
The cotangent function is defined only when the denominator is not zero.
\( \sin \theta \ne 0 \)
Since \( \sin \theta = 0 \) at angles of the form
\( \theta = k\pi \), where \( k \) is an integer,
the cotangent function is undefined at these values and has vertical asymptotes there.
The cotangent function has the same period as the tangent function, which is
\( \pi \).
The range of the cotangent function is
\( (-\infty, \infty) \).
Example:
Evaluate \( \cot\!\left(\dfrac{\pi}{4}\right) \).
▶️ Answer/Explanation
Using sine and cosine values,
\( \sin\!\left(\dfrac{\pi}{4}\right) = \dfrac{\sqrt{2}}{2} \)
\( \cos\!\left(\dfrac{\pi}{4}\right) = \dfrac{\sqrt{2}}{2} \)
Now compute the ratio:
\( \cot\!\left(\dfrac{\pi}{4}\right) = \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \)
Example:
Determine where the function \( y = \cot \theta \) is undefined.
▶️ Answer/Explanation
The cotangent function is undefined when \( \sin \theta = 0 \).
\( \theta = k\pi \), where \( k \) is any integer.
Conclusion: \( y = \cot \theta \) has vertical asymptotes at these values.
Graphical Behavior of the Cotangent Function
The cotangent function
\( f(\theta) = \cot \theta \) 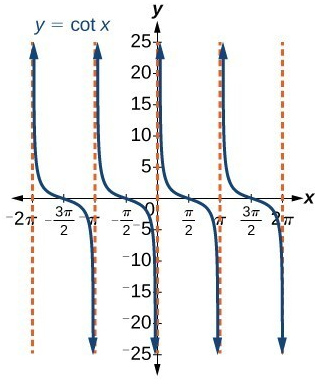
has vertical asymptotes at domain values where the tangent function equals zero.
Since
\( \tan \theta = 0 \) when \( \theta = k\pi \), where \( k \) is an integer,
the graph of \( y = \cot \theta \) has vertical asymptotes at
\( \theta = k\pi \)
Between any two consecutive asymptotes, the cotangent function is strictly decreasing.
This decreasing behavior repeats every period of the function, which is
\( \pi \).
As \( \theta \) approaches a vertical asymptote from the left, the output values increase without bound, and as \( \theta \) approaches the asymptote from the right, the output values decrease without bound.
Example:
State the vertical asymptotes of the function \( y = \cot \theta \).
▶️ Answer/Explanation
Vertical asymptotes occur where \( \tan \theta = 0 \).
\( \theta = k\pi \), where \( k \) is any integer.
Final answer: The vertical asymptotes are at \( \theta = k\pi \).
Example:
Describe the behavior of \( y = \cot \theta \) on the interval
\( (0, \pi) \).
▶️ Answer/Explanation
The interval \( (0, \pi) \) lies between two consecutive asymptotes at \( \theta = 0 \) and \( \theta = \pi \).
On this interval, the cotangent function decreases continuously.
As \( \theta \to 0^+ \), \( \cot \theta \to \infty \).
As \( \theta \to \pi^- \), \( \cot \theta \to -\infty \).
Conclusion: \( y = \cot \theta \) is decreasing between consecutive asymptotes.
