AP Precalculus -3.12 Equivalent Trigonometric Forms- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.12 Equivalent Trigonometric Forms- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.12 Equivalent Trigonometric Forms- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The function $ f $ is defined by $ f(\theta) = \cos(2\theta) $. Which is an equivalent expression for $ f(\theta) $?

(A) 1
(B) $ 1 – 2\cos^2\theta $
(C) $ 1 – 2\sin^2\theta $
(D) $ 2\cos\theta\sin\theta $

▶️ Answer/Explanation

Detailed solution

Using the double-angle identity:
$ \cos(2\theta) = \cos^2\theta – \sin^2\theta $.
Replace $ \cos^2\theta = 1 – \sin^2\theta $:
$ \cos(2\theta) = (1 – \sin^2\theta) – \sin^2\theta = 1 – 2\sin^2\theta $.
✅ Answer: (C)

Question

On the unit circle, first angle $ \theta $ gives point $(a, b)$. Second angle $ 2\theta $ gives $(c, d)$. Express $ c, d $ in terms of $ a, b $.

(A) $ c = -b, d = -a $
(B) $ c = 2a, d = 2b $
(C) $ c = a^2 + b^2, d = 2ab $
(D) $ c = a^2 – b^2, d = 2ab $

▶️ Answer/Explanation

Detailed solution

On unit circle: $ a = \cos\theta, b = \sin\theta $.
Then $ c = \cos(2\theta) = \cos^2\theta – \sin^2\theta = a^2 – b^2 $.
$ d = \sin(2\theta) = 2\sin\theta\cos\theta = 2ab $.
✅ Answer: (D)

Question

The function $ f(x) = \cos x (1 + \tan^2 x) $. Which expression is equivalent to $ f(x) $?

(A) $ \sec x $
(B) $ \cos^3 x $
(C) $ \tan x \sec x $
(D) $ \cot x \csc x $

▶️ Answer/Explanation

Detailed solution

Using $ 1 + \tan^2 x = \sec^2 x $:
$ f(x) = \cos x \cdot \sec^2 x = \cos x \cdot \frac{1}{\cos^2 x} = \frac{1}{\cos x} = \sec x $.
✅ Answer: (A)

Question

Right triangle: hypotenuse = 1, side opposite angle $ \frac{5\pi}{12} $ has length $ x $. Given $ \frac{5\pi}{12} = \frac{3\pi}{12} + \frac{2\pi}{12} $, find $ x $.

(A) $ \left( \frac{\sqrt{2}}{2} \right) \left( \frac{\sqrt{2}}{2} \right) + \left( \frac{1}{2} \right) \left( \frac{\sqrt{3}}{2} \right) $
(B) $ \left( \frac{\sqrt{2}}{2} \right) \left( \frac{\sqrt{3}}{2} \right) + \left( \frac{\sqrt{2}}{2} \right) \left( \frac{1}{2} \right) $
(C) $ \left( \frac{\sqrt{2}}{2} \right) \left( \frac{\sqrt{3}}{2} \right) – \left( \frac{\sqrt{2}}{2} \right) \left( \frac{1}{2} \right) $
(D) $ \left( \frac{\sqrt{2}}{2} \right) \left( \frac{1}{2} \right) – \left( \frac{\sqrt{2}}{2} \right) \left( \frac{\sqrt{3}}{2} \right) $

▶️ Answer/Explanation

Detailed solution

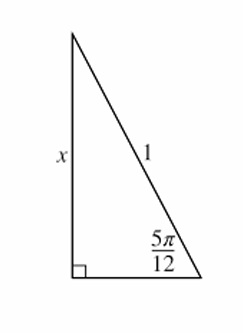
$ x = \sin\frac{5\pi}{12} $.
Let $ \frac{3\pi}{12} = \frac{\pi}{4} $, $ \frac{2\pi}{12} = \frac{\pi}{6} $.
Using sum identity: $ \sin\left(\frac{\pi}{4} + \frac{\pi}{6}\right) = \sin\frac{\pi}{4}\cos\frac{\pi}{6} + \cos\frac{\pi}{4}\sin\frac{\pi}{6} $.
$ \sin\frac{\pi}{4} = \frac{\sqrt{2}}{2}, \cos\frac{\pi}{6} = \frac{\sqrt{3}}{2} $, $ \cos\frac{\pi}{4} = \frac{\sqrt{2}}{2}, \sin\frac{\pi}{6} = \frac{1}{2} $.
Thus $ x = \left(\frac{\sqrt{2}}{2}\right)\left(\frac{\sqrt{3}}{2}\right) + \left(\frac{\sqrt{2}}{2}\right)\left(\frac{1}{2}\right) $.
✅ Answer: (B)

Question

The identity $ \sin(x + \frac{\pi}{2}) = \cos x $ shows cosine is a horizontal translation of sine. Which identity verifies this directly?

(A) The sum identity for sine
(B) The sum identity for cosine
(C) The double-angle identity for sine
(D) The double-angle identity for cosine

▶️ Answer/Explanation

Detailed solution

The sum identity for sine: $ \sin(A + B) = \sin A \cos B + \cos A \sin B $.
Let $ A = x, B = \frac{\pi}{2} $:
$ \sin(x + \frac{\pi}{2}) = \sin x \cos\frac{\pi}{2} + \cos x \sin\frac{\pi}{2} $.
Since $ \cos\frac{\pi}{2} = 0 $ and $ \sin\frac{\pi}{2} = 1 $, we get $ \cos x $.
✅ Answer: (A)

Question

The function $ g(x) = 7\sin(2x) $. Which is an equivalent form?

(A) $ 14\cos x \sin x $
(B) $ (7\cos x)(7\sin x) $
(C) $ 7\cos^2 x – 7\sin^2 x $
(D) $ 7 – 14\sin^2 x $

▶️ Answer/Explanation

Detailed solution

Using the double-angle identity: $ \sin(2x) = 2\sin x \cos x $.
Thus $ g(x) = 7 \cdot 2\sin x \cos x = 14\sin x \cos x $.
✅ Answer: (A)

Question

Where both expressions are defined, which of the following is equivalent to $\frac{\sec^{2}x-1}{\sec^{2}x}$?

(A) $\frac{\tan^{2}x}{\sin^{2}x}$
(B) $\frac{\tan^{2}x}{\cos^{2}x}$
(C) $\sin^{2}x$
(D) $\cos^{2}x$

▶️ Answer/Explanation

Detailed solution

1. Use Pythagorean Identity:
$\sec^2 x – 1 = \tan^2 x$.

2. Simplify Fraction:
$\frac{\tan^2 x}{\sec^2 x} = \tan^2 x \cdot \cos^2 x$
$= \frac{\sin^2 x}{\cos^2 x} \cdot \cos^2 x = \sin^2 x$

✅ Answer: (C)

Question

The function $ g $ is given by $ g(x) = 7 \sin(2x) $. Which of the following is an equivalent form for $ g(x) $?

(A) $ g(x) = 14 \cos x \sin x $
(B) $ g(x) = (7 \cos x)(7 \sin x) $
(C) $ g(x) = 7 \cos^2 x – 7 \sin^2 x $
(D) $ g(x) = 7 – 14 \sin^2 x $

▶️ Answer/Explanation

Detailed solution

Using the double-angle identity:
\[ \sin(2x) = 2 \sin x \cos x \]
Thus, \[ g(x) = 7 \sin(2x) = 7 \cdot 2 \sin x \cos x = 14 \sin x \cos x \]
This matches option (A).
✅ Answer: (A)

Question

Where both expressions are defined, which of the following is equivalent to $\frac{\sec^2 x – 1}{\sec^2 x}$?

(A) $\frac{\tan^2 x}{\sin^2 x}$

(B) $\frac{\tan^2 x}{\cos^2 x}$

(D) $\sin^2 x$

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

Step 1: Identify the Pythagorean identity in the numerator. We know that $\tan^2 x + 1 = \sec^2 x$, therefore $\sec^2 x – 1 = \tan^2 x$.
Step 2: Substitute this into the expression: $\frac{\tan^2 x}{\sec^2 x}$.
Step 3: Rewrite in terms of sine and cosine: $\tan^2 x = \frac{\sin^2 x}{\cos^2 x}$ and $\sec^2 x = \frac{1}{\cos^2 x}$.
Step 4: Divide the fractions: $\frac{\sin^2 x}{\cos^2 x} \div \frac{1}{\cos^2 x} = \frac{\sin^2 x}{\cos^2 x} \cdot \cos^2 x$.
Step 5: Cancel the $\cos^2 x$ terms to get the final result: $\sin^2 x$.

Question

The function of $h$ is given by $h(x) = \sin \left(\beta + \frac{\pi}{3}\right)$, where $0 < \beta < \frac{\pi}{2}$. Which of the following is an equivalent form for $h(x)$?

(A) $\frac{1}{2} \sin \beta + \frac{\sqrt{3}}{3} \cos \beta$

(B) $\frac{1}{2} \sin \beta – \frac{\sqrt{3}}{2} \cos \beta$

(D) $\sin \beta + \frac{\sqrt{3}}{2}$

▶️ Answer/Explanation

Detailed solution

The problem asks for the expansion of the expression $h(x) = \sin \left(\beta + \frac{\pi}{3}\right)$. This requires the sine addition formula:

$\sin(A + B) = \sin A \cos B + \cos A \sin B$

Here, we substitute $A = \beta$ and $B = \frac{\pi}{3}$:

$h(x) = \sin \beta \cos \left(\frac{\pi}{3}\right) + \cos \beta \sin \left(\frac{\pi}{3}\right)$

Next, substitute the exact trigonometric values for the angle $\frac{\pi}{3}$ ($60^\circ$):

$\cos \left(\frac{\pi}{3}\right) = \frac{1}{2}$

$\sin \left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}$

Replacing these values back into the equation:

$h(x) = \sin \beta \left(\frac{1}{2}\right) + \cos \beta \left(\frac{\sqrt{3}}{2}\right)$

Rearranging the terms gives:

$h(x) = \frac{1}{2} \sin \beta + \frac{\sqrt{3}}{2} \cos \beta$

Comparing this result with the options, it corresponds to the form in Option (A). (Note: The option in the image shows $\frac{\sqrt{3}}{3}$, which is likely a typographical error for $\frac{\sqrt{3}}{2}$).

Question

The functions $ g $ and $ h $ are given by:
$$ g(x) = 2 \log a – 3 \log b + \frac{\log a}{2} + \log (100 c) $$
$$ h(x) = \cot x \sec^{2} x – \tan x $$

(A) i. Rewrite $ g(x) $ as a single logarithm with base 10 without negative exponents in any part of the expression. Your result should be simplified in the form $ \log(\text{expression}) $.
ii. Rewrite $ h(x) $ as an expression in which $ \cot x $ appears once and no other trigonometric functions are involved.

(B) The functions $ j $ and $ k $ are given by:
$$ j(x) = 3 \cot^{2} \theta + 3 \csc \theta $$
$$ k(x) = 7 e^{-2x} + 9 $$

i. Solve $ j(x) = -3 $ for values of $ x $ in the interval $ [0, 2\pi) $.
ii. Solve $ k(x) = 86 $ for all values of $ x $ in the domain of $ k $.

(C) Two functions $ a $ and $ b $ are given by:
$$ a(x) = 3 – 3 \csc 3\theta $$
$$ b(x) = -1 + \csc 3\theta $$

Find all the input values in the domain of $ a $ and $ b $ where $ a(x) $ and $ b(x) $ intersect.

Most-appropriate topic codes (CED):

• TOPIC 2.12: Logarithmic Function Manipulation — part (A) i
• TOPIC 3.11: Equivalent Representations of Trigonometric Functions — part (A) ii
• TOPIC 3.12: Trigonometric Equation Solving — part (B) i
• TOPIC 2.13: Exponential and Logarithmic Equations and Inequalities — part (B) ii
• TOPIC 3.12: Trigonometric Equation Solving — part (C)

▶️ Answer/Explanation

Detailed solution

(A) i. Logarithmic Simplification
Start with the given expression:
$ g(x) = 2 \log a + \frac{1}{2} \log a – 3 \log b + \log (100 c) $

Combine the $ \log a $ terms ($ 2 + 0.5 = 2.5 $):
$ \frac{5}{2} \log a – 3 \log b + \log (100 c) $

Use power rules to move coefficients inside the logarithms:
$ \log (a^{5/2}) – \log (b^3) + \log (100 c) $

Combine using product and quotient rules:
$ \log \left( \frac{100 c \cdot a^{5/2}}{b^3} \right) $

Final Answer: $ \log \left( \frac{100 a^{5/2} c}{b^3} \right) $

(A) ii. Trigonometric Simplification
Start with: $ h(x) = \cot x \sec^2 x – \tan x $

Convert to sine and cosine:
$ \left(\frac{\cos x}{\sin x}\right) \cdot \left(\frac{1}{\cos^2 x}\right) – \frac{\sin x}{\cos x} $

Simplify the first term:
$ \frac{1}{\sin x \cos x} – \frac{\sin x}{\cos x} $

Find a common denominator ($ \sin x \cos x $) and simplify:
$ \frac{1 – \sin^2 x}{\sin x \cos x} = \frac{\cos^2 x}{\sin x \cos x} $

Cancel terms:
$ \frac{\cos x}{\sin x} $

Final Answer: $ \cot x $

(B) i. Trigonometric Equation
Set $ j(x) = -3 $:
$ 3 \cot^2 \theta + 3 \csc \theta = -3 $

Divide by 3 and rearrange:
$ \cot^2 \theta + \csc \theta + 1 = 0 $

Substitute identity $ \cot^2 \theta = \csc^2 \theta – 1 $:
$ (\csc^2 \theta – 1) + \csc \theta + 1 = 0 $
$ \csc^2 \theta + \csc \theta = 0 $

Factor:
$ \csc \theta (\csc \theta + 1) = 0 $

Solve $ \csc \theta = -1 $ (since $ \csc \theta \neq 0 $):
$ \sin \theta = -1 $

[Image of unit circle sine values]

In the interval $ [0, 2\pi) $:
Final Answer: $ \theta = \frac{3\pi}{2} $

(B) ii. Exponential Equation
Set $ k(x) = 86 $:
$ 7 e^{-2x} + 9 = 86 $

Subtract 9 and divide by 7:
$ 7 e^{-2x} = 77 \implies e^{-2x} = 11 $

Take the natural log:
$ -2x = \ln 11 $

Final Answer: $ x = -\frac{1}{2} \ln 11 $

(C) Intersection
Set $ a(x) = b(x) $:
$ 3 – 3 \csc 3\theta = -1 + \csc 3\theta $

Rearrange:
$ 4 = 4 \csc 3\theta \implies \csc 3\theta = 1 $

So, $ \sin 3\theta = 1 $. The sine function equals 1 at $ \frac{\pi}{2} $ plus full rotations:
$ 3\theta = \frac{\pi}{2} + 2k\pi $

Final Answer: $ \theta = \frac{\pi}{6} + \frac{2k\pi}{3} $, where $ k \in \mathbb{Z} $

Question

Directions:

Unless otherwise specified, the domain of a function $ f $ is assumed to be the set of all real numbers $ x $ for which $ f(x) $ is a real number. Angle measures for trigonometric functions are assumed to be in radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be obtained without a calculator. For example, $ \log_2 8 $, $ \cos(\frac{\pi}{2}) $, and $ \sin^{-1}(1) $ can be evaluated without a calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and logarithms, where applicable. For example, $ 2x + 3x $, $ 5^2 \cdot 5^3 $, $ \frac{x^5}{x^2} $, and $ \ln 3 + \ln 5 $ should be rewritten in equivalent forms.
For each part of the question, show the work that leads to your answers.

Part A
The functions $ g $ and $ h $ are given by

$ g(x) = \log_5(4x – 2) $
$ h(x) = \sin^{-1}(8x) $

(i) Solve $ g(x) = 3 $ for values of $ x $ in the domain of $ g $.

(ii) Solve $ h(x) = \frac{\pi}{4} $ for values of $ x $ in the domain of $ h $.

Part B
The functions $ j $ and $ k $ are given by

$ j(x) = (\sec x)(\cot x) $
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $

(i) Rewrite $ j(x) $ as an expression involving $ \sin x $ and no other trigonometric functions.

(ii) Rewrite $ k(x) $ as an expression of the form $ 4^{(ax+b)} $, where $ a $ and $ b $ are constants.

Part C
The function $ m $ is given by

$ m(x) = \sqrt{3}\tan(x + \frac{\pi}{2}) $.

Find all values in the domain of $ m $ that yield an output value of 1.

▶️ Answer/Explanation

Detailed solution

Part A
(i) Solve $ g(x) = 3 $
Start with the given equation:
$ \log_5(4x – 2) = 3 $
Convert the logarithmic equation to exponential form ($ y = \log_b x \iff x = b^y $):
$ 4x – 2 = 5^3 $
Evaluate the exponent:
$ 4x – 2 = 125 $
Add 2 to both sides:
$ 4x = 127 $
Divide by 4:
$ x = \frac{127}{4} $

(ii) Solve $ h(x) = \frac{\pi}{4} $
Start with the given equation:
$ \sin^{-1}(8x) = \frac{\pi}{4} $
Take the sine of both sides to isolate the argument:
$ 8x = \sin\left(\frac{\pi}{4}\right) $
Substitute the exact value of $ \sin\left(\frac{\pi}{4}\right) $:
$ 8x = \frac{\sqrt{2}}{2} $
Divide by 8:
$ x = \frac{\sqrt{2}}{16} $

Part B
(i) Rewrite $ j(x) $
Start with the function definition:
$ j(x) = (\sec x)(\cot x) $
Substitute the reciprocal and quotient identities ($ \sec x = \frac{1}{\cos x} $ and $ \cot x = \frac{\cos x}{\sin x} $):
$ j(x) = \left(\frac{1}{\cos x}\right) \left(\frac{\cos x}{\sin x}\right) $
Cancel the $ \cos x $ terms:
$ j(x) = \frac{1}{\sin x} $

(ii) Rewrite $ k(x) $
Start with the function definition:
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $
To write in the form $ 4^{(ax+b)} $, convert bases 16 and 2 to base 4.
Since $ 16 = 4^2 $ and $ 2 = \sqrt{4} = 4^{1/2} = 4^{0.5} $:
$ k(x) = \frac{(4^2)^{3x} \cdot 4^x}{4^{0.5}} $
Apply the power of a power rule ($ (a^m)^n = a^{mn} $):
$ k(x) = \frac{4^{6x} \cdot 4^x}{4^{0.5}} $
Apply the product rule for exponents ($ a^m \cdot a^n = a^{m+n} $) in the numerator:
$ k(x) = \frac{4^{6x + x}}{4^{0.5}} = \frac{4^{7x}}{4^{0.5}} $
Apply the quotient rule for exponents ($ \frac{a^m}{a^n} = a^{m-n} $):
$ k(x) = 4^{7x – 0.5} $ (or $ 4^{7x – \frac{1}{2}} $)
Thus, $ a = 7 $ and $ b = -0.5 $.

Part C
Find values where $ m(x) = 1 $
Set the function equal to 1:
$ \sqrt{3}\tan\left(x + \frac{\pi}{2}\right) = 1 $
Isolate the tangent function by dividing by $ \sqrt{3} $:
$ \tan\left(x + \frac{\pi}{2}\right) = \frac{1}{\sqrt{3}} $
Determine the reference angle. We know that $ \tan\left(\frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} $.
Set up the general solution for tangent ($ \theta = \text{ref} + n\pi $):
$ x + \frac{\pi}{2} = \frac{\pi}{6} + n\pi $, where $ n $ is any integer.
Solve for $ x $ by subtracting $ \frac{\pi}{2} $ from both sides:
$ x = \frac{\pi}{6} – \frac{\pi}{2} + n\pi $
Find a common denominator (6) to combine fractions:
$ x = \frac{\pi}{6} – \frac{3\pi}{6} + n\pi $
$ x = -\frac{2\pi}{6} + n\pi $
Simplify the fraction:
$ x = -\frac{\pi}{3} + n\pi $

Question

Directions:

Unless otherwise specified, the domain of a function $ f $ is assumed to be the set of all real numbers $ x $ for which $ f(x) $ is a real number. Angle measures for trigonometric functions are assumed to be in radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be obtained without a calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and logarithms where applicable.
For each part of the question, show the work that leads to your answers.

(A) The functions $ g $ and $ h $ are given by

$ g(x) = 3^{(2x)} \cdot 3^{(x+4)} $
$ h(x) = 2\tan^2 x – 1 $

(i) Solve $ g(x) = 27 $ for values of $ x $ in the domain of $ g $.
(ii) Solve $ h(x) = 5 $ for values of $ x $ in the interval $ [0, 2\pi) $.

(B) The functions $ j $ and $ k $ are given by

$ j(x) = 2\log_{10}(x+3) – \log_{10} x – \log_{10} 3 $
$ k(x) = \frac{(\tan^2 x)(\cot x)}{\csc x} $

(i) Rewrite $ j(x) $ as a single logarithm base 10 without negative exponents in any part of the expression. Your result should be of the form $ \log_{10}(\text{expression}) $.
(ii) Rewrite $ k(x) $ as a fraction involving $ \sec x $ and no other trigonometric functions.

$ m(x) = \frac{2^{(5x+3)}}{\left(2^{(x-2)}\right)^3} $

Find all input values in the domain of $ m $ that yield an output value of $ \frac{1}{16} $.

▶️ Answer/Explanation

Detailed Solution

(A)(i) Solve $ g(x) = 27 $

First, simplify the expression for $ g(x) $ using the property of exponents $ a^m \cdot a^n = a^{m+n} $.
$ g(x) = 3^{2x} \cdot 3^{x+4} = 3^{(2x + x + 4)} = 3^{(3x+4)} $
Set $ g(x) $ equal to 27 and rewrite 27 as a base of 3:
$ 3^{(3x+4)} = 27 $
$ 3^{(3x+4)} = 3^3 $
Since the bases are equal, the exponents must be equal:
$ 3x + 4 = 3 $
$ 3x = 3 – 4 $
$ 3x = -1 $
$ x = -\frac{1}{3} $

(A)(ii) Solve $ h(x) = 5 $ on $ [0, 2\pi) $

Set the expression for $ h(x) $ equal to 5:
$ 2\tan^2 x – 1 = 5 $
Add 1 to both sides:
$ 2\tan^2 x = 6 $
Divide by 2:
$ \tan^2 x = 3 $
Take the square root of both sides:
$ \tan x = \pm\sqrt{3} $
The reference angle for $ \tan \theta = \sqrt{3} $ is $ \frac{\pi}{3} $.
Since we have $ \pm\sqrt{3} $, we must consider solutions in all four quadrants within the interval $ [0, 2\pi) $:
Quadrant I: $ x = \frac{\pi}{3} $
Quadrant II: $ x = \pi – \frac{\pi}{3} = \frac{2\pi}{3} $
Quadrant III: $ x = \pi + \frac{\pi}{3} = \frac{4\pi}{3} $
Quadrant IV: $ x = 2\pi – \frac{\pi}{3} = \frac{5\pi}{3} $
Solution set: $ x = \frac{\pi}{3}, \frac{2\pi}{3}, \frac{4\pi}{3}, \frac{5\pi}{3} $

(B)(i) Rewrite $ j(x) $ as a single logarithm

Given: $ j(x) = 2\log_{10}(x+3) – \log_{10} x – \log_{10} 3 $
Use the power rule $ n\log a = \log(a^n) $:
$ = \log_{10}((x+3)^2) – \log_{10} x – \log_{10} 3 $
Factor out the negative sign for the last two terms to group them:
$ = \log_{10}((x+3)^2) – (\log_{10} x + \log_{10} 3) $
Use the product rule $ \log a + \log b = \log(ab) $:
$ = \log_{10}((x+3)^2) – \log_{10}(3x) $
Use the quotient rule $ \log a – \log b = \log(\frac{a}{b}) $:
$ = \log_{10}\left(\frac{(x+3)^2}{3x}\right) $

(B)(ii) Rewrite $ k(x) $ involving $ \sec x $

Given: $ k(x) = \frac{(\tan^2 x)(\cot x)}{\csc x} $
First, simplify the numerator using $ \tan x \cdot \cot x = 1 $:
$ (\tan^2 x)(\cot x) = \tan x \cdot (\tan x \cdot \cot x) = \tan x \cdot 1 = \tan x $
Now substitute back into the expression:
$ k(x) = \frac{\tan x}{\csc x} $
Convert to sine and cosine:
$ = \frac{\frac{\sin x}{\cos x}}{\frac{1}{\sin x}} $
$ = \frac{\sin x}{\cos x} \cdot \frac{\sin x}{1} = \frac{\sin^2 x}{\cos x} $
We need the expression in terms of $ \sec x $. Use the identity $ \sin^2 x = 1 – \cos^2 x $:
$ = \frac{1 – \cos^2 x}{\cos x} $
Substitute $ \cos x = \frac{1}{\sec x} $:
$ = \frac{1 – \left(\frac{1}{\sec x}\right)^2}{\frac{1}{\sec x}} $
$ = \frac{1 – \frac{1}{\sec^2 x}}{\frac{1}{\sec x}} $
Find a common denominator for the numerator:
$ = \frac{\frac{\sec^2 x – 1}{\sec^2 x}}{\frac{1}{\sec x}} $
Multiply by the reciprocal of the denominator:
$ = \frac{\sec^2 x – 1}{\sec^2 x} \cdot \frac{\sec x}{1} $
$ = \frac{\sec^2 x – 1}{\sec x} $

(C) Find input values for $ m(x) = \frac{1}{16} $

First, simplify the expression for $ m(x) $:
$ m(x) = \frac{2^{(5x+3)}}{\left(2^{(x-2)}\right)^3} $
Simplify the denominator using the power rule $ (a^m)^n = a^{m \cdot n} $:
$ \left(2^{(x-2)}\right)^3 = 2^{3(x-2)} = 2^{3x-6} $
Now apply the quotient rule $ \frac{a^m}{a^n} = a^{m-n} $:
$ m(x) = \frac{2^{5x+3}}{2^{3x-6}} = 2^{(5x+3) – (3x-6)} $
$ = 2^{5x + 3 – 3x + 6} $
$ = 2^{2x + 9} $
Set $ m(x) = \frac{1}{16} $ and rewrite $ \frac{1}{16} $ as a power of 2:
$ \frac{1}{16} = \frac{1}{2^4} = 2^{-4} $
Equate the simplified $ m(x) $ to $ 2^{-4} $:
$ 2^{2x + 9} = 2^{-4} $
Equate the exponents:
$ 2x + 9 = -4 $
$ 2x = -13 $
$ x = -\frac{13}{2} $ or $ -6.5 $

Question

(A) The function $g$ and $h$ are given by

$g(x) = 3 \ln x – \frac{1}{2} \ln x$

$h(x) = \frac{\sin^2 x – 1}{\cos x}$

(i) Rewrite $g(x)$ as a single natural logarithm without negative exponents in any part of the expression. Your result should be of the form $\ln(\text{expression})$.
(ii) Rewrite $h(x)$ as an expression in which $\cos x$ appears once and no other trigonometric functions are involved.

(B) The functions $j$ and $k$ are given by

$j(x) = 2(\sin x)(\cos x)$

$k(x) = 8e^{(3x)} – e$

(i) Solve $j(x) = 0$ for values of $x$ in the interval $\left[0, \frac{\pi}{2}\right]$.
(ii) Solve $k(x) = 3e$ for values of $x$ in the domain of $k$.

$m(x) = \cos(2x) + 4$

Find all input values in the domain of $m$ that yield an output of $\frac{9}{2}$.

▶️ Answer/Explanation

Detailed solution

(A)(i) Rewrite $g(x)$

The function is given by $g(x) = 3 \ln x – \frac{1}{2} \ln x$.
Combine the like terms:
$g(x) = \left(3 – \frac{1}{2}\right) \ln x$
$g(x) = \frac{5}{2} \ln x$
Apply the power property of logarithms, $a \ln b = \ln(b^a)$:
$g(x) = \ln\left(x^{5/2}\right)$

(A)(ii) Rewrite $h(x)$

The function is given by $h(x) = \frac{\sin^2 x – 1}{\cos x}$.
Recall the Pythagorean identity: $\sin^2 x + \cos^2 x = 1$.
Rearrange the identity to isolate the numerator expression: $\sin^2 x – 1 = -\cos^2 x$.
Substitute this into the function:
$h(x) = \frac{-\cos^2 x}{\cos x}$
Simplify the expression by canceling one $\cos x$ term:
$h(x) = -\cos x$

(B)(i) Solve $j(x) = 0$

Set the function equal to zero: $2(\sin x)(\cos x) = 0$.
Divide both sides by 2:
$\sin x \cos x = 0$
By the zero product property, either $\sin x = 0$ or $\cos x = 0$.
Case 1: $\sin x = 0$. In the interval $\left[0, \frac{\pi}{2}\right]$, $x = 0$.
Case 2: $\cos x = 0$. In the interval $\left[0, \frac{\pi}{2}\right]$, $x = \frac{\pi}{2}$.
The solutions are $x = 0$ and $x = \frac{\pi}{2}$.

(B)(ii) Solve $k(x) = 3e$

Set the function equal to $3e$:
$8e^{(3x)} – e = 3e$
Add $e$ to both sides:
$8e^{(3x)} = 4e$
Divide both sides by 8:
$e^{(3x)} = \frac{4e}{8}$
$e^{(3x)} = \frac{e}{2}$
Take the natural logarithm ($\ln$) of both sides:
$\ln\left(e^{3x}\right) = \ln\left(\frac{e}{2}\right)$
Use logarithm properties to simplify ($\ln(e^a) = a$ and $\ln(a/b) = \ln a – \ln b$):
$3x = \ln e – \ln 2$
Since $\ln e = 1$:
$3x = 1 – \ln 2$
Divide by 3:
$x = \frac{1 – \ln 2}{3}$

(C) Find input values for $m(x) = \frac{9}{2}$

Set the function equal to $\frac{9}{2}$:
$\cos(2x) + 4 = \frac{9}{2}$
Subtract 4 from both sides (note that $4 = \frac{8}{2}$):
$\cos(2x) = \frac{9}{2} – \frac{8}{2}$
$\cos(2x) = \frac{1}{2}$
The reference angle for cosine equal to $\frac{1}{2}$ is $\frac{\pi}{3}$.
The general solution for $2x$ is:
$2x = \frac{\pi}{3} + 2\pi n$ or $2x = -\frac{\pi}{3} + 2\pi n$ (where $n$ is an integer).
Solve for $x$ by dividing by 2:
$x = \frac{\pi}{6} + \pi n$ or $x = -\frac{\pi}{6} + \pi n$
Combining these, the input values are $x = \pm \frac{\pi}{6} + \pi n$ for any integer $n$.

AP Precalculus -3.12 Equivalent Trigonometric Forms- MCQ Exam Style Questions - Effective Fall 2023