AP Precalculus -3.12 Equivalent Trigonometric Forms- Study Notes - Effective Fall 2023
AP Precalculus -3.12 Equivalent Trigonometric Forms- Study Notes – Effective Fall 2023
AP Precalculus -3.12 Equivalent Trigonometric Forms- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Rewrite trigonometric expressions in equivalent forms with the Pythagorean identity.
Rewrite trigonometric expressions in equivalent forms with sine and cosine sum identities.
Solve equations using equivalent analytic representations of trigonometric functions.
Key Concepts:
The Pythagorean Identity
Using the Pythagorean Identity to Derive Other Trigonometric Relationships
Sum Identities for Sine and Cosine
Difference and Double-Angle Identities
Verifying Trigonometric Identities
Solving Trigonometric Equations Using Equivalent Analytic Representations
The Pythagorean Identity
The Pythagorean Theorem can be applied to right triangles formed on the unit circle.
For an angle \( \theta \) in standard position, the point on the unit circle where the terminal ray intersects the circle has coordinates![]()
\( (\cos \theta, \sin \theta) \)
Because the radius of the unit circle is 1, the distance from the origin to this point is 1.
Applying the Pythagorean Theorem to the right triangle formed by the x-coordinate, y-coordinate, and the radius gives
\( (\cos \theta)^2 + (\sin \theta)^2 = 1^2 \)
This simplifies to the Pythagorean identity:
\( \sin^2 \theta + \cos^2 \theta = 1 \)
This identity is true for all real values of \( \theta \) and is fundamental in trigonometry.
Example:
Verify the Pythagorean identity for \( \theta = \dfrac{\pi}{3} \).
▶️ Answer/Explanation
Compute the sine and cosine values:
\( \sin\!\left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2} \)
\( \cos\!\left(\dfrac{\pi}{3}\right) = \dfrac{1}{2} \)
Substitute into the identity:
\( \left(\dfrac{\sqrt{3}}{2}\right)^2 + \left(\dfrac{1}{2}\right)^2 = \dfrac{3}{4} + \dfrac{1}{4} = 1 \)
Conclusion: The identity is verified.
Example:
Use the Pythagorean identity to find \( \cos \theta \) if \( \sin \theta = \dfrac{3}{5} \) and \( \theta \) lies in Quadrant II.
▶️ Answer/Explanation
Start with the identity:
\( \sin^2 \theta + \cos^2 \theta = 1 \)
Substitute \( \sin \theta = \dfrac{3}{5} \):
\( \left(\dfrac{3}{5}\right)^2 + \cos^2 \theta = 1 \)
\( \dfrac{9}{25} + \cos^2 \theta = 1 \)
Solve for \( \cos^2 \theta \):
\( \cos^2 \theta = \dfrac{16}{25} \)
Since \( \theta \) is in Quadrant II, cosine is negative.
\( \cos \theta = -\dfrac{4}{5} \)
Final answer: \( \cos \theta = -\dfrac{4}{5} \).
Using the Pythagorean Identity to Derive Other Trigonometric Relationships
The Pythagorean identity
\( \sin^2 \theta + \cos^2 \theta = 1 \)
can be algebraically manipulated to produce additional identities involving other trigonometric functions.
Deriving an Identity Involving Tangent and Secant
Divide both sides of the Pythagorean identity by \( \cos^2 \theta \), assuming \( \cos \theta \ne 0 \).
\( \dfrac{\sin^2 \theta}{\cos^2 \theta} + \dfrac{\cos^2 \theta}{\cos^2 \theta} = \dfrac{1}{\cos^2 \theta} \)
This simplifies to
\( \tan^2 \theta + 1 = \sec^2 \theta \)
Rewriting gives the identity
\( \tan^2 \theta = \sec^2 \theta – 1 \)
This identity is valid for all \( \theta \) where the expressions are defined.
Establishing Relationships Between Inverse Trigonometric Functions
The Pythagorean identity can also be used to establish relationships between inverse trigonometric functions.
If
\( \theta = \arcsin x \)
then
\( \sin \theta = x \)
Using the Pythagorean identity,
\( \cos \theta = \sqrt{1 – x^2} \)
provided \( \theta \) lies in the restricted range of the arcsine function.
Therefore, with appropriate domain restrictions,
\( \arcsin x = \arccos(\sqrt{1 – x^2}) \)
This relationship holds when
\( 0 \le x \le 1 \)
so that the square root is defined and the angle lies in the correct principal ranges.
Example:
Verify the identity
\( \tan^2 \theta = \sec^2 \theta – 1 \)
for \( \theta = \dfrac{\pi}{4} \).
▶️ Answer/Explanation
Compute each side.
\( \tan\!\left(\dfrac{\pi}{4}\right) = 1 \Rightarrow \tan^2\!\left(\dfrac{\pi}{4}\right) = 1 \)
\( \sec\!\left(\dfrac{\pi}{4}\right) = \sqrt{2} \Rightarrow \sec^2\!\left(\dfrac{\pi}{4}\right) – 1 = 2 – 1 = 1 \)
Conclusion: Both sides are equal, so the identity is verified.
Example:
Evaluate
\( \arccos(\sqrt{1 – x^2}) \)
when \( x = \dfrac{1}{2} \).
▶️ Answer/Explanation
\( \sqrt{1 – \left(\dfrac{1}{2}\right)^2} = \sqrt{\dfrac{3}{4}} = \dfrac{\sqrt{3}}{2} \)
Now find the angle in \( [0, \pi] \) whose cosine is \( \dfrac{\sqrt{3}}{2} \).
\( \arccos\!\left(\dfrac{\sqrt{3}}{2}\right) = \dfrac{\pi}{6} \)
Conclusion: This matches \( \arcsin\!\left(\dfrac{1}{2}\right) = \dfrac{\pi}{6} \), confirming the relationship.
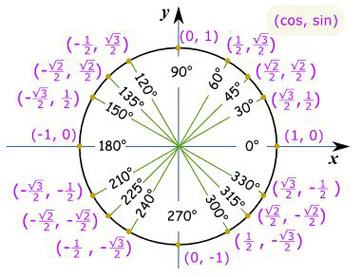
Sum Identities for Sine and Cosine
The sum identities allow trigonometric expressions involving the sum of two angles to be rewritten in terms of the sine and cosine of the individual angles.
Sine Sum Identity
\( \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \)
Cosine Sum Identity
\( \cos(\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \)
These identities are valid for all real values of \( \alpha \) and \( \beta \).
They are especially useful for:
- finding exact trigonometric values
- rewriting trigonometric expressions
- deriving other trigonometric identities
Example:
Use the sine sum identity to find the exact value of
\( \sin\!\left(\dfrac{5\pi}{12}\right) \).
▶️ Answer/Explanation
Write \( \dfrac{5\pi}{12} \) as a sum of angles:
\( \dfrac{5\pi}{12} = \dfrac{\pi}{4} + \dfrac{\pi}{6} \)
Apply the sine sum identity:
\( \sin\!\left(\dfrac{\pi}{4} + \dfrac{\pi}{6}\right) = \sin\dfrac{\pi}{4}\cos\dfrac{\pi}{6} + \cos\dfrac{\pi}{4}\sin\dfrac{\pi}{6} \)
Substitute known values:
\( = \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2} \)
\( = \dfrac{\sqrt{6} + \sqrt{2}}{4} \)
Example:
Use the cosine sum identity to evaluate
\( \cos\!\left(\dfrac{3\pi}{4} + \dfrac{\pi}{6}\right) \).
▶️ Answer/Explanation
Apply the cosine sum identity:
\( \cos\!\left(\dfrac{3\pi}{4} + \dfrac{\pi}{6}\right) = \cos\dfrac{3\pi}{4}\cos\dfrac{\pi}{6} – \sin\dfrac{3\pi}{4}\sin\dfrac{\pi}{6} \)
Substitute known values:
\( = \left(-\dfrac{\sqrt{2}}{2}\right)\!\left(\dfrac{\sqrt{3}}{2}\right) – \left(\dfrac{\sqrt{2}}{2}\right)\!\left(\dfrac{1}{2}\right) \)
\( = -\dfrac{\sqrt{6} + \sqrt{2}}{4} \)
Difference and Double-Angle Identities
The sum identities for sine and cosine can be adapted to create difference identities and double-angle identities.
These identities are obtained by choosing specific values for the angles in the sum formulas.
Difference Identities
Replacing \( \beta \) with \( -\beta \) in the sum identities gives the difference identities.
\( \sin(\alpha – \beta) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \)
\( \cos(\alpha – \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \)
Double-Angle Identities
Setting \( \alpha = \beta = \theta \) in the sum identities produces the double-angle identities.
\( \sin(2\theta) = 2\sin \theta \cos \theta \)
\( \cos(2\theta) = \cos^2 \theta – \sin^2 \theta \)
Using the Pythagorean identity, the cosine double-angle identity can also be written as
\( \cos(2\theta) = 1 – 2\sin^2 \theta \)
\( \cos(2\theta) = 2\cos^2 \theta – 1 \)
These identities are useful for simplifying expressions and finding exact trigonometric values.
Example:
Use a difference identity to find the exact value of
\( \sin\!\left(\dfrac{\pi}{3} – \dfrac{\pi}{6}\right) \).
▶️ Answer/Explanation
Apply the sine difference identity:
\( \sin(\alpha – \beta) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \)
Substitute values:
\( \sin\dfrac{\pi}{3}\cos\dfrac{\pi}{6} – \cos\dfrac{\pi}{3}\sin\dfrac{\pi}{6} \)
\( = \dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{3}}{2} – \dfrac{1}{2}\cdot\dfrac{1}{2} \)
\( = \dfrac{3 – 1}{4} = \dfrac{1}{2} \)
Example:
Use a double-angle identity to find the exact value of
\( \cos\!\left(\dfrac{\pi}{3}\right) \) given that \( \theta = \dfrac{\pi}{6} \).
▶️ Answer/Explanation
Since \( \dfrac{\pi}{3} = 2\left(\dfrac{\pi}{6}\right) \), use the cosine double-angle identity:
\( \cos(2\theta) = 2\cos^2 \theta – 1 \)
Substitute \( \cos\dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2} \):
\( 2\left(\dfrac{\sqrt{3}}{2}\right)^2 – 1 = 2\cdot\dfrac{3}{4} – 1 = \dfrac{1}{2} \)
Final answer: \( \cos\!\left(\dfrac{\pi}{3}\right) = \dfrac{1}{2} \).
Verifying Trigonometric Identities
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variable for which both sides are defined.
To verify a trigonometric identity, properties of trigonometric functions, known trigonometric identities, and algebraic techniques are used.
Common Strategies for Verification
Use reciprocal identities, such as \( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \)
Apply Pythagorean identities, such as \( \sin^2 \theta + \cos^2 \theta = 1 \)
Use sum, difference, and double-angle identities
Simplify algebraically by factoring, combining like terms, or finding common denominators
When verifying identities, it is important to manipulate only one side of the equation until it matches the other side.
Example:
Verify the identity
\( \dfrac{1}{\cos \theta} – \cos \theta = \dfrac{\sin^2 \theta}{\cos \theta} \).
▶️ Answer/Explanation
Start with the left-hand side:
\( \dfrac{1}{\cos \theta} – \cos \theta \)
Write both terms with a common denominator:
\( \dfrac{1 – \cos^2 \theta}{\cos \theta} \)
Apply the Pythagorean identity \( 1 – \cos^2 \theta = \sin^2 \theta \):
\( \dfrac{\sin^2 \theta}{\cos \theta} \)
Conclusion: The left-hand side simplifies to the right-hand side, so the identity is verified.
Example:
Verify the identity
\( \tan \theta + \cot \theta = \sec \theta \csc \theta \).
▶️ Answer/Explanation
Rewrite tangent and cotangent using sine and cosine:
\( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \)
\( \cot \theta = \dfrac{\cos \theta}{\sin \theta} \)
Add the fractions:
\( \dfrac{\sin^2 \theta + \cos^2 \theta}{\sin \theta \cos \theta} \)
Apply the Pythagorean identity:
\( \dfrac{1}{\sin \theta \cos \theta} \)
Rewrite using reciprocal identities:
\( \sec \theta \csc \theta \)
Conclusion: The identity is verified.
Solving Trigonometric Equations Using Equivalent Analytic Representations
Trigonometric equations and inequalities can often be solved more efficiently by rewriting expressions using equivalent analytic representations.
Equivalent forms use known identities and relationships between trigonometric functions while preserving the original meaning of the expression.
Choosing an appropriate equivalent form can make important information more accessible, such as:
- zeros and solutions
- domain restrictions
- simpler algebraic structure
Common equivalent representations include:
- reciprocal identities, such as \( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \)
- Pythagorean identities, such as \( \sin^2 \theta + \cos^2 \theta = 1 \)
- sum, difference, and double-angle identities
Using these equivalent forms allows trigonometric equations and inequalities to be reduced to simpler equations that can be solved algebraically.
Example:
Solve the equation
\( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \)
for \( 0 \le \theta < 2\pi \).
▶️ Answer/Explanation
Using the reciprocal identity, the equation becomes
\( \tan \theta = \tan \theta \)
This equation is true for all values of \( \theta \) where tangent is defined.
Since \( \tan \theta \) is undefined at \( \theta = \dfrac{\pi}{2} + k\pi \), those values must be excluded.
Final answer: All \( \theta \) in \( [0,2\pi) \) except \( \dfrac{\pi}{2} \) and \( \dfrac{3\pi}{2} \).
Example:
Solve the equation
\( \sin^2 \theta = 1 – \cos^2 \theta \)
for \( 0 \le \theta < 2\pi \).
▶️ Answer/Explanation
Using the Pythagorean identity, the equation becomes
\( \sin^2 \theta = \sin^2 \theta \)
This equation is true for all values of \( \theta \).
Therefore, every value of \( \theta \) in the interval satisfies the equation.
Final answer: All \( \theta \) in \( [0, 2\pi) \).
