AP Precalculus -3.15 Rates of Change in Polar Functions- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.15 Rates of Change in Polar Functions- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.15 Rates of Change in Polar Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

Consider the graph of the polar function $ r = f(\theta) $, where $ f(\theta) = 4\sin(2\theta) $, in the polar coordinate system. On the interval $ 0 \leq \theta \leq 2\pi $, which of the following is true about the graph of $ r = f(\theta) $?

(A) For the input values $ \theta = \frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \frac{7\pi}{4} $, the function $ r = f(\theta) $ has extrema that correspond to points that are farthest from the origin.
(B) For the input values $ \theta = \frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \frac{7\pi}{4} $, the function $ r = f(\theta) $ has extrema. However, only the points corresponding to $ \theta = \frac{\pi}{4} $ and $ \theta = \frac{5\pi}{4} $ are farthest from the origin.
(C) For the input values $ \theta = \frac{\pi}{2} $ and $ \theta = \frac{3\pi}{2} $, the function $ r = f(\theta) $ has extrema that correspond to points that are farthest from the origin.
(D) For the input values $ \theta = \frac{\pi}{2} $ and $ \theta = \frac{3\pi}{2} $, the function $ r = f(\theta) $ has extrema. However, only the point corresponding to $ \theta = \frac{\pi}{2} $ is farthest from the origin.

▶️ Answer/Explanation

Detailed solution

For $ r = 4\sin(2\theta) $, the extrema occur where $ \sin(2\theta) = \pm 1 $.
This happens when $ 2\theta = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, \frac{7\pi}{2} $, so $ \theta = \frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \frac{7\pi}{4} $.
At these angles, $ r = 4 $ or $ r = -4 $, but the distance from the origin is $ |r| = 4 $ in all four cases, so they are all farthest from the origin.
✅ Answer: (A)

Question

Consider the graph of the polar function $ r = f(\theta) $, where $ f(\theta) = 1 + 2 \sin \theta $, in the polar coordinate system for $ 0 \leq \theta \leq 2\pi $. Which of the following statements is true about the distance between the point with polar coordinates $ (f(\theta), \theta) $ and the origin?

(A) The distance is increasing for $ 0 \leq \theta \leq \frac{\pi}{2} $, because $ f(\theta) $ is positive and increasing on the interval.
(B) The distance is increasing for $ \frac{3\pi}{2} \leq \theta \leq \frac{11\pi}{6} $, because $ f(\theta) $ is negative and increasing on the interval.
(C) The distance is decreasing for $ 0 \leq \theta \leq \frac{\pi}{2} $, because $ f(\theta) $ is positive and decreasing on the interval.
(D) The distance is decreasing for $ \frac{3\pi}{2} \leq \theta \leq \frac{11\pi}{6} $, because $ f(\theta) $ is negative and decreasing on the interval.

▶️ Answer/Explanation

Detailed solution

In polar coordinates, the distance from the origin is given by $ r = f(\theta) $. However, distance must be non-negative. When $ f(\theta) $ is negative, the point is plotted $ |f(\theta)| $ units in the opposite direction, but the distance from the origin is $ |f(\theta)| $.

We check each option:

On $ 0 \leq \theta \leq \frac{\pi}{2} $: $ f'(\theta) = 2 \cos \theta > 0 $ (increasing), and $ f(\theta) > 0 $, so distance $ = f(\theta) $ is increasing. ✅ (A) is correct.
On $ \frac{3\pi}{2} \leq \theta \leq \frac{11\pi}{6} $: $ f(\theta) = 1 + 2 \sin \theta $. For $ \theta = \frac{3\pi}{2} $, $ f(\theta) = -1 $; for $ \theta = \frac{11\pi}{6} $, $ f(\theta) = 0 $. Since $ f(\theta) $ is negative and increasing toward 0, $ |f(\theta)| $ is decreasing. So the distance is decreasing, not increasing. (B) is false.
(C) contradicts (A), so false.
(D) states “because $ f(\theta) $ is negative and decreasing” — but $ f(\theta) $ is increasing here, not decreasing, so false.

✅ Answer: (A)

Question

A polar function is given by $ r = f(\theta) = -1 + \sin \theta $. As $\theta$ increases on the interval $0 < \theta < \frac{\pi}{2}$, which of the following is true about the points on the graph of $r = f(\theta)$ in the $xy$-plane?

(A) The points on the graph are above the $x$-axis and are getting closer to the origin.
(B) The points on the graph are above the $x$-axis and are getting farther from the origin.
(C) The points on the graph are below the $x$-axis and are getting closer to the origin.
(D) The points on the graph are below the $x$-axis and are getting farther from the origin.

▶️ Answer/Explanation

Detailed solution

For $0 < \theta < \frac{\pi}{2}$, $\sin \theta$ increases from 0 to 1.
Thus $f(\theta) = -1 + \sin \theta$ increases from $-1$ to $0$.
Since $f(\theta)$ is negative, points are in the direction opposite to terminal ray $\theta$; i.e., for $0 < \theta < \frac{\pi}{2}$, the corresponding Cartesian points lie in Quadrant IV (below the $x$-axis).
The distance from origin is $ |f(\theta)| = 1 – \sin \theta$, which decreases as $\theta$ increases.
✅ Answer: (C)

Question

Consider the graph of the polar function $ r = f(\theta) $, where $ f(\theta) = \theta (\theta – 2)(\theta – 4) $, in the polar coordinate system for $ 0 \leq \theta \leq 4 $. Which of the following statements is true?

(A) On the interval $ 2 < \theta < 2.1 $, the distance between $ (f(\theta), \theta) $ and the origin is increasing because the values of $ f(\theta) $ are negative and decreasing.
(B) On the interval $ 2 < \theta < 2.1 $, the distance between $ (f(\theta), \theta) $ and the origin is decreasing because the values of $ f(\theta) $ are negative and decreasing.
(C) On the interval $ 2 < \theta < 2.1 $, the distance between $ (f(\theta), \theta) $ and the origin is increasing because the values of $ f(\theta) $ are negative and increasing.
(D) On the interval $ 2 < \theta < 2.1 $, the distance between $ (f(\theta), \theta) $ and the origin is decreasing because the values of $ f(\theta) $ are negative and increasing.

▶️ Answer/Explanation

Detailed solution

For $ 2 < \theta < 2.1 $:
$ \theta > 0 $, $ \theta – 2 > 0 $, $ \theta – 4 < 0 $ ⇒ $ f(\theta) = \theta(\theta-2)(\theta-4) < 0 $.

Check derivative: $ f'(\theta) = (\theta-2)(\theta-4) + \theta(\theta-4) + \theta(\theta-2) $.
At $ \theta = 2 $, $ f'(2) = -4 < 0 $, so $ f $ is decreasing near $ \theta = 2 $.
Thus on $ 2 < \theta < 2.1 $, $ f(\theta) $ is negative and decreasing.

Distance from origin = $ |f(\theta)| = -f(\theta) $.
Since $ f $ is decreasing (more negative), $ |f| $ is increasing.
Therefore, distance is increasing.
✅ Answer: (A)

Question

Consider the graph of the polar function $ r = f(\theta) $, where $ f(\theta) = 2 \sin \theta – 1 $, in the polar coordinate system. Which of the following descriptions is true?

(A) As $ \theta $ increases from 0 to $ \frac{\pi}{6} $, the polar function $ r = f(\theta) $ is increasing, and the distance between the point $ (f(\theta), \theta) $ on the curve and the origin is increasing.
(B) As $ \theta $ increases from 0 to $ \frac{\pi}{6} $, the polar function $ r = f(\theta) $ is increasing, and the distance between the point $ (f(\theta), \theta) $ on the curve and the origin is decreasing.
(C) As $ \theta $ increases from 0 to $ \frac{\pi}{6} $, the polar function $ r = f(\theta) $ is decreasing, and the distance between the point $ (f(\theta), \theta) $ on the curve and the origin is increasing.
(D) As $ \theta $ increases from 0 to $ \frac{\pi}{6} $, the polar function $ r = f(\theta) $ is decreasing, and the distance between the point $ (f(\theta), \theta) $ on the curve and the origin is decreasing.

▶️ Answer/Explanation

Detailed solution

On $ 0 \leq \theta \leq \frac{\pi}{6} $:
$ f(\theta) = 2\sin\theta – 1 $.
Since $ \sin\theta $ increases from 0 to $ \frac12 $, $ f(\theta) $ increases from $ -1 $ to $ 0 $.
So $ f $ is increasing.

Also $ f(\theta) $ is negative (or zero at $ \theta = \frac{\pi}{6} $).
Distance from origin = $ |f(\theta)| = 1 – 2\sin\theta $.
As $ \theta $ increases, $ 1 – 2\sin\theta $ decreases.
Thus the distance is decreasing.

Conclusion: $ f(\theta) $ is increasing, distance is decreasing.
✅ Answer: (B)

Question

The polar function $r=f(\theta)$, where $f(\theta)=1+2\cos\theta$, is graphed in the polar coordinate system for $0\le\theta\le2\pi$ On which of the following intervals of $\theta$ is the distance between the point with polar coordinates $(f(\theta),\theta)$ and the origin decreasing?

(A) $(0,2.094)$ only
(B) $(2.094,4.189)$
(C) $(0,2.094)$ and $(3.142,4.189)$
(D) $(2.094,3.142)$ and $(4.189,6.283)$

▶️ Answer/Explanation

Detailed solution

1. Define the distance:
The distance from the origin is given by $|r| = |1+2\cos\theta|$. The distance decreases when $r$ moves towards 0.

2. Find where $r=0$:
$1+2\cos\theta = 0 \implies \cos\theta = -0.5$.
$\theta \approx 2.094$ ($\frac{2\pi}{3}$) and $\theta \approx 4.189$ ($\frac{4\pi}{3}$).

3. Analyze the intervals:
• Interval $(0, 2.094)$: $r$ decreases from $3$ to $0$. (Distance decreases).
• Interval $(3.142, 4.189)$ (which is $\pi$ to $\frac{4\pi}{3}$): $r$ increases from $-1$ to $0$. Since $r$ is negative and approaching 0, the absolute value (distance) is decreasing.

✅ Answer: (C)

Question

▶️ Answer/Explanation

Detailed solution

Distance from origin = $ |r| = |f(\theta)| $.
On $ 0 \leq \theta \leq \frac{\pi}{2} $:
$ f(\theta) = 1 + 2\sin\theta $ is positive (since $\sin\theta \ge 0$) and increasing (since $\sin\theta$ increases). So $ |f(\theta)| = f(\theta) $ increases ⇒ distance increases.
Thus (A) is true.
Check others:
On $ \frac{3\pi}{2} \leq \theta \leq \frac{11\pi}{6} $: $ \sin\theta $ increases from -1 to -0.5, so $ f(\theta) = 1+2\sin\theta $ increases from -1 to 0, but it’s negative, so $ |f(\theta)| $ decreases (from 1 to 0) ⇒ distance decreases, not increases. (B) false.
(C) and (D) contradict sign/monotonicity analysis.
✅ Answer: (A)

Question

In the function $r = f(\theta)$, $f\left(\frac{\pi}{4}\right) = 2$. If the rate of change is $-3$ and is changing at a rate of $2$ at $\frac{\pi}{4} < \theta < \frac{\pi}{2}$, then which one of the following can be a possible value of $f\left(\frac{\pi}{3}\right)$?

a. $r = 2$
b. $r = 5$
c. $r = 1$
d. $r = -1$

▶️ Answer/Explanation

Detailed solution

Given $f\left(\frac{\pi}{4}\right) = 2$, $f’\left(\frac{\pi}{4}\right) = -3$, and $f”(\theta) = 2$.
Let $\Delta \theta = \frac{\pi}{3} – \frac{\pi}{4} = \frac{\pi}{12} \approx 0.2618$.
Using the Taylor expansion: $f(\theta) \approx f(a) + f'(a)(\Delta \theta) + \frac{1}{2}f”(a)(\Delta \theta)^2$.
Substitute the values: $f\left(\frac{\pi}{3}\right) \approx 2 + (-3)\left(\frac{\pi}{12}\right) + \frac{1}{2}(2)\left(\frac{\pi}{12}\right)^2$.
$f\left(\frac{\pi}{3}\right) \approx 2 – 0.7854 + 0.0685$.
$f\left(\frac{\pi}{3}\right) \approx 1.2831$.
Among the given choices, $r = 1$ is the closest possible value.
Correct Option: c

Question

In the polar coordinate system, the graph of a polar function $r = f(\theta)$ is shown with a domain of all real values of $\theta$ for $0 \le \theta \le 2\pi$. On this following interval of $\theta$, the graph has no holes, passes through each point exactly one time, and as $\theta$ increases, the graph passes through the labeled points $A, B, C,$ and $D$, in that order. On which of the following intervals is the average rate of change of $r$ with respect to $\theta$ greatest?

(A) From $A$ to $C$

(B) From $B$ to $C$

(D) From $C$ to $D$

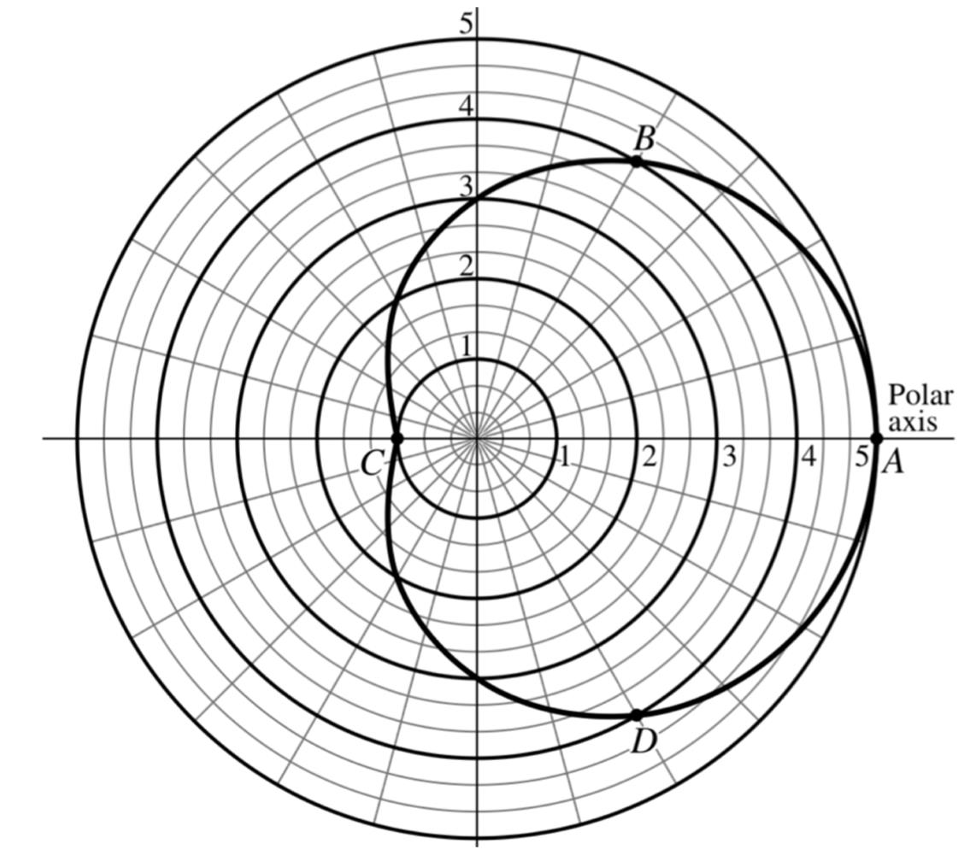
▶️ Answer/Explanation

Detailed solution

The average rate of change of $r$ with respect to $\theta$ is given by the ratio: $$\frac{\Delta r}{\Delta \theta} = \frac{r_{final} – r_{initial}}{\theta_{final} – \theta_{initial}}$$

Based on the grid, we can estimate the radius $r$ at each point:
• A: $r = 5$
• B: $r \approx 4$
• C: $r = 1$
• D: $r \approx 4$

For intervals (A) From $A$ to $C$ and (B) From $B$ to $C$, the radius $r$ decreases ($5 \to 1$ and $4 \to 1$), so the rate of change is negative.

For interval (C) From $B$ to $D$, the radius starts at $r \approx 4$ and returns to $r \approx 4$, meaning the net change $\Delta r$ is near zero, so the rate is approximately zero.

For interval (D) From $C$ to $D$, the radius increases from $r = 1$ to $r \approx 4$. Since $\Delta r > 0$ and $\Delta \theta > 0$, the rate of change is positive.

Since a positive value is greater than zero or a negative value, the greatest average rate of change occurs on the interval from $C$ to $D$.

Question

Consider the graph of the polar function $r = f(\theta)$, where $\theta$ is increasing in the polar coordinate system on the interval $0 \leq \theta \leq 2\pi$. Given that $f(\theta) < 0$ and decreasing on the interval $\pi \leq \theta \leq \frac{3\pi}{2}$, which of the following statements is true about the distance between polar coordinates $(f(\theta), \theta)$ and the origin?

(A) The distance is increasing for $0 \leq \theta \leq 2\pi$.

(B) The distance is decreasing for $0 \leq \theta \leq 2\pi$.

(D) The distance is decreasing for $\pi \leq \theta \leq \frac{3\pi}{2}$.

▶️ Answer/Explanation

Detailed solution

The correct answer is (C).

The distance from the origin to a polar point $(r, \theta)$ is given by $|r| = |f(\theta)|$.
On the interval $\pi \leq \theta \leq \frac{3\pi}{2}$, we are given that $f(\theta) < 0$, so the distance is $d(\theta) = -f(\theta)$.
We are also given that $f(\theta)$ is decreasing, which implies its derivative is negative: $f'(\theta) < 0$.
To find how the distance changes, we differentiate $d(\theta)$ with respect to $\theta$: $d'(\theta) = -f'(\theta)$.
Since $f'(\theta)$ is negative, $-f'(\theta)$ must be positive, meaning $d'(\theta) > 0$.
A positive derivative indicates an increasing function, so the distance is increasing on this interval.

Question

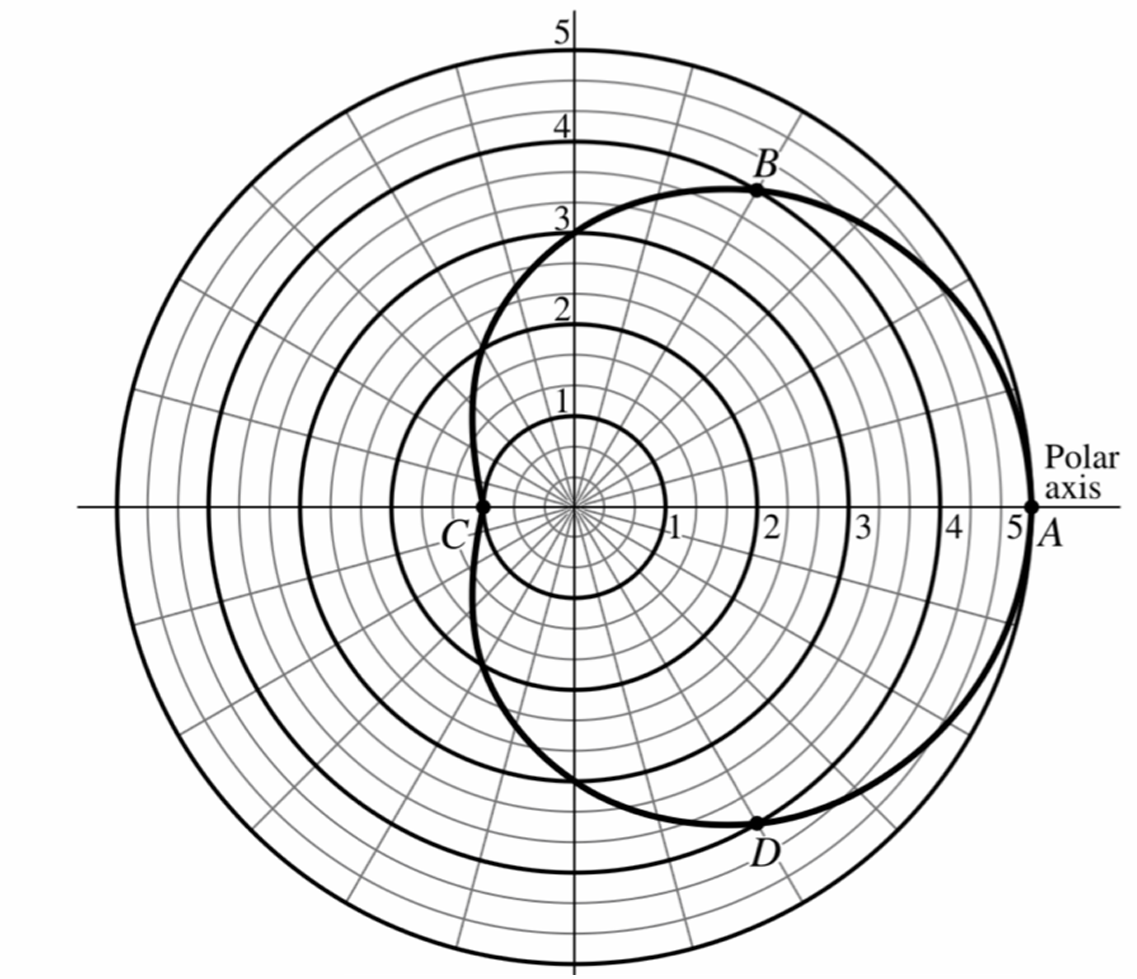
In the polar coordinate system, the graph of a polar function $r = f(\theta)$ is shown with a domain of all real values of $\theta$ for $0 \le \theta < 2\pi$. On this interval of $\theta$, the graph has no holes, passes through each point exactly one time, and as $\theta$ increases, the graph passes through the labeled points $A, B, C,$ and $D$, in that order. On which of the following intervals is the average rate of change of $r$ with respect to $\theta$ greatest?

(A) From $A$ to $C$
(B) From $B$ to $C$
(C) From $B$ to $D$
(D) From $C$ to $D$

▶️ Answer/Explanation

Detailed solution

The average rate of change of $r$ with respect to $\theta$ is given by the formula $\frac{\Delta r}{\Delta \theta} = \frac{r_2 – r_1}{\theta_2 – \theta_1}$.
Point $C$ is at the smallest radius ($r \approx 1$) and point $D$ is at a much larger radius ($r \approx 4.5$).
From $C$ to $D$, the value of $r$ increases significantly over a relatively small change in angle $\Delta \theta$.
In intervals (A) and (B), the radius $r$ is decreasing, resulting in a negative average rate of change.
In interval (C), the radius increases from $B$ ($r \approx 3.5$) to $D$ ($r \approx 4.5$), but over a much larger $\Delta \theta$.
Therefore, the steep positive increase in radius per radian occurs from $C$ to $D$.
The average rate of change is greatest on the interval from $C$ to $D$.
Correct Option: (D)

AP Precalculus -3.15 Rates of Change in Polar Functions- MCQ Exam Style Questions - Effective Fall 2023