AP Precalculus -3.2 Sine, Cosine, and Tangent- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -3.2 Sine, Cosine, and Tangent- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -3.2 Sine, Cosine, and Tangent- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
▶️ Answer/Explanation
For a point on a circle of radius \( r = 4 \) at angle \( \theta = \frac{5\pi}{6} \):
\( x = r \cos\theta = 4 \cos\left(\frac{5\pi}{6}\right) = 4 \cdot \left(-\frac{\sqrt{3}}{2}\right) = -2\sqrt{3} \)
\( y = r \sin\theta = 4 \sin\left(\frac{5\pi}{6}\right) = 4 \cdot \frac{1}{2} = 2 \)
Thus, the intersection point is \( (-2\sqrt{3}, 2) \), which is in Quadrant II.
✅ Answer: (A)
▶️ Answer/Explanation
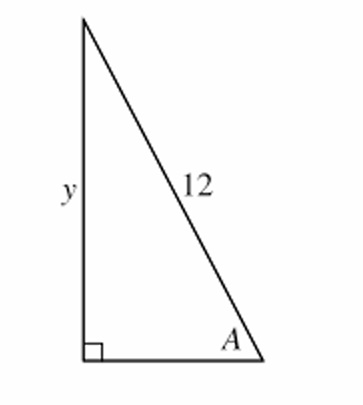
In a right triangle, the sine of angle \( A \) is the ratio of the opposite side \( y \) to the hypotenuse. From the figure, the hypotenuse is 12, so \( \sin A = \frac{y}{12} \).
To express \( A \) as a function of \( y \), we take the inverse sine: \( A = \sin^{-1}\left(\frac{y}{12}\right) \).
Thus, \( f(y) = \sin^{-1}\left(\frac{y}{12}\right) \).
✅ Answer: (D)
▶️ Answer/Explanation
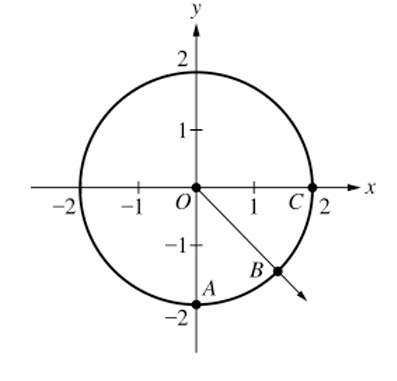
From the figure (assuming standard positions):
– Angle \( AOB \) is measured from positive x-axis to ray \( OB \).
– Given \( \angle COB = \angle AOB \), and likely \( A \) is on positive x-axis, \( C \) is on positive y-axis or similar.
– If \( OA \) is along positive x-axis, \( OC \) along positive y-axis, then \( \angle AOB = \angle COB \) implies \( OB \) bisects the quadrant.
For Quadrant IV: \( OB \) at \( \frac{7\pi}{4} \) (if starting from +x, rotating clockwise to match symmetry).
Radius is 2, so coordinates: \( (2\cos\frac{7\pi}{4}, 2\sin\frac{7\pi}{4}) \).
✅ Answer: (C)
▶️ Answer/Explanation
Points:
\( A: (20\cos\frac{2\pi}{3}, 20\sin\frac{2\pi}{3}) = \left(20\cdot\left(-\frac12\right), 20\cdot\frac{\sqrt{3}}{2}\right) = (-10, 10\sqrt{3}) \)
\( B: (20\cos\frac{4\pi}{3}, 20\sin\frac{4\pi}{3}) = \left(20\cdot\left(-\frac12\right), 20\cdot\left(-\frac{\sqrt{3}}{2}\right)\right) = (-10, -10\sqrt{3}) \)
The points are vertically aligned (same \( x \)-coordinate).
Distance = \( |10\sqrt{3} – (-10\sqrt{3})| = 20\sqrt{3} \).
That’s equal to \( 20\sin\frac{2\pi}{3} – 20\sin\frac{4\pi}{3} \) because:
\( 20\sin\frac{2\pi}{3} = 20\cdot\frac{\sqrt{3}}{2} = 10\sqrt{3} \)
\( 20\sin\frac{4\pi}{3} = 20\cdot\left(-\frac{\sqrt{3}}{2}\right) = -10\sqrt{3} \)
Difference: \( 10\sqrt{3} – (-10\sqrt{3}) = 20\sqrt{3} \), which is the vertical distance.
✅ Answer: (D)
▶️ Answer/Explanation
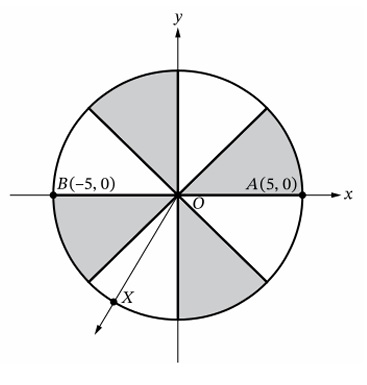
Given \( X = \left(-\frac{5}{2}, -\frac{5\sqrt{3}}{2}\right) \).
Radius \( r = \sqrt{\left(\frac{5}{2}\right)^2 + \left(\frac{5\sqrt{3}}{2}\right)^2} = \sqrt{\frac{25}{4}+\frac{75}{4}} = \sqrt{25} = 5 \).
The coordinates match \( \left(5\cdot\left(-\frac12\right), 5\cdot\left(-\frac{\sqrt{3}}{2}\right)\right) \), so \( \cos\theta = -\frac12, \sin\theta = -\frac{\sqrt{3}}{2} \).
That’s \( \theta = \frac{4\pi}{3} \) (Quadrant III).
\( B \) is at angle \( \pi \) (since it’s at \((-5,0)\)).
Angle \( XOB \) = \( \theta_X – \theta_B = \frac{4\pi}{3} – \pi = \frac{\pi}{3} \).
✅ Answer: (B)
▶️ Answer/Explanation
The slope of the terminal ray of an angle in standard position is given by \( \tan\theta \).
For \( \theta = \frac{\pi}{3} \), \( \tan\left(\frac{\pi}{3}\right) = \sqrt{3} \).
✅ Answer: (D)
▶️ Answer/Explanation
Tangent = \( \frac{y}{x} = \frac{-0.9}{0.4} = -\frac{9}{4} \).
Slope of terminal ray = tangent = \( -\frac{9}{4} \).
✅ Answer: (C)
▶️ Answer/Explanation
1. Condition for Coterminal Angles:
Angles share a terminal ray if their difference is a multiple of \(2\pi\).
2. Check Option (C):
\(\frac{8\pi}{3} – \frac{2\pi}{3} = \frac{6\pi}{3} = 2\pi\).
Since the difference is exactly \(2\pi\), they are coterminal.
✅ Answer: (C)
▶️ Answer/Explanation
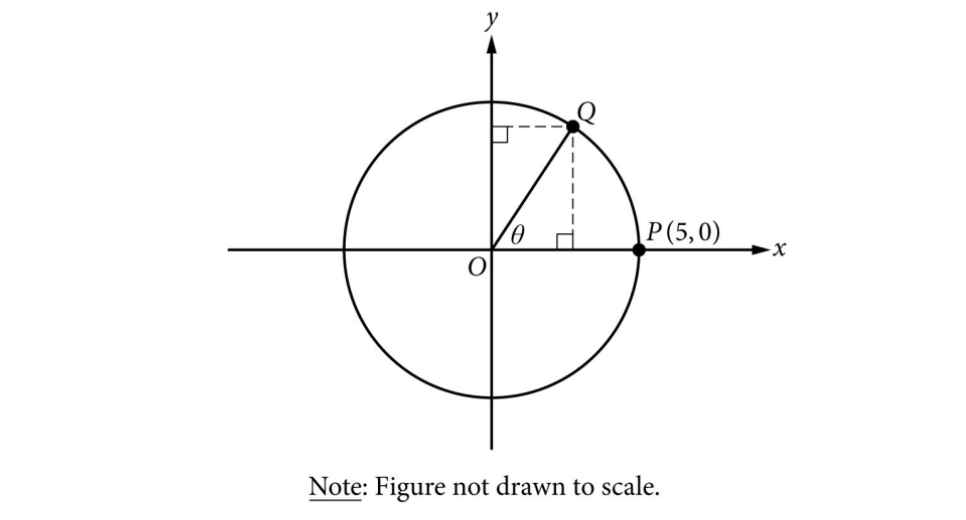
1. Determine the Radius:
Point \(P\) is at \((5,0)\) and is on the circle. Thus, the radius \(r = 5\).
2. Determine the Angle \(\theta\):
The arc length formula is \(s = r\theta\).
Given \(s = 6\) and \(r = 5\), we have \(6 = 5\theta\), so \(\theta = \frac{6}{5}\) radians.
3. Find the Distance from the Y-axis:
The distance of a point \((x, y)\) from the y-axis is \(|x|\).
The x-coordinate of point \(Q\) is \(x = r\cos\theta = 5\cos(\frac{6}{5})\).
Therefore, the distance is \(5\cos(\frac{6}{5})\).
✅ Answer: (C)
▶️ Answer/Explanation
1. Definition:
Slope \(m\) of terminal ray = \(\tan\theta\).
2. Calculation:
Given \(\tan\theta = -\frac{3}{4}\).
Slope \(m = -\frac{3}{4}\).
✅ Answer: (C)
▶️ Answer/Explanation
Identify the coordinates of the given point: \(x = \sqrt{17}\) and \(y = -8\).
Recall the trigonometric ratio for tangent: \(\tan \theta = \frac{y}{x}\).
Substitute the values: \(\tan \theta = \frac{-8}{\sqrt{17}}\).
Rationalize the denominator by multiplying the top and bottom by \(\sqrt{17}\).
Calculation: \(\frac{-8 \cdot \sqrt{17}}{\sqrt{17} \cdot \sqrt{17}} = -\frac{8\sqrt{17}}{17}\).
Compare the result with the given choices.
The correct option is d.
▶️ Answer/Explanation
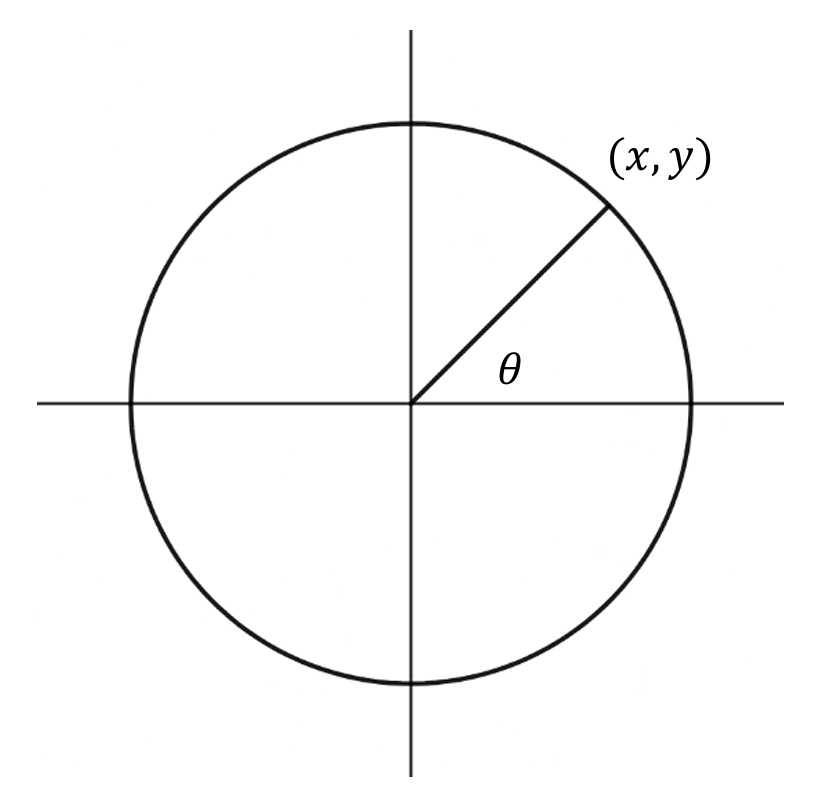
The slope of the radial line from the origin $(0,0)$ to the terminal point is $m_{radius} = \tan(\theta)$.
Substituting the given angle, the radial slope is $m_{radius} = \tan\left(\frac{\pi}{5}\right) \approx 0.7265$.
A tangent line to a circle is perpendicular to the radius at the point of contact.
Perpendicular slopes are negative reciprocals: $m_{tangent} = -\frac{1}{m_{radius}}$.
Thus, $m_{tangent} = -\frac{1}{\tan(\pi/5)} = -\cot\left(\frac{\pi}{5}\right)$.
Calculating the value: $-\frac{1}{0.7265} \approx -1.376$.
Rounding to two decimal places, the slope is $-1.38$.
The correct option is b.
▶️ Answer/Explanation
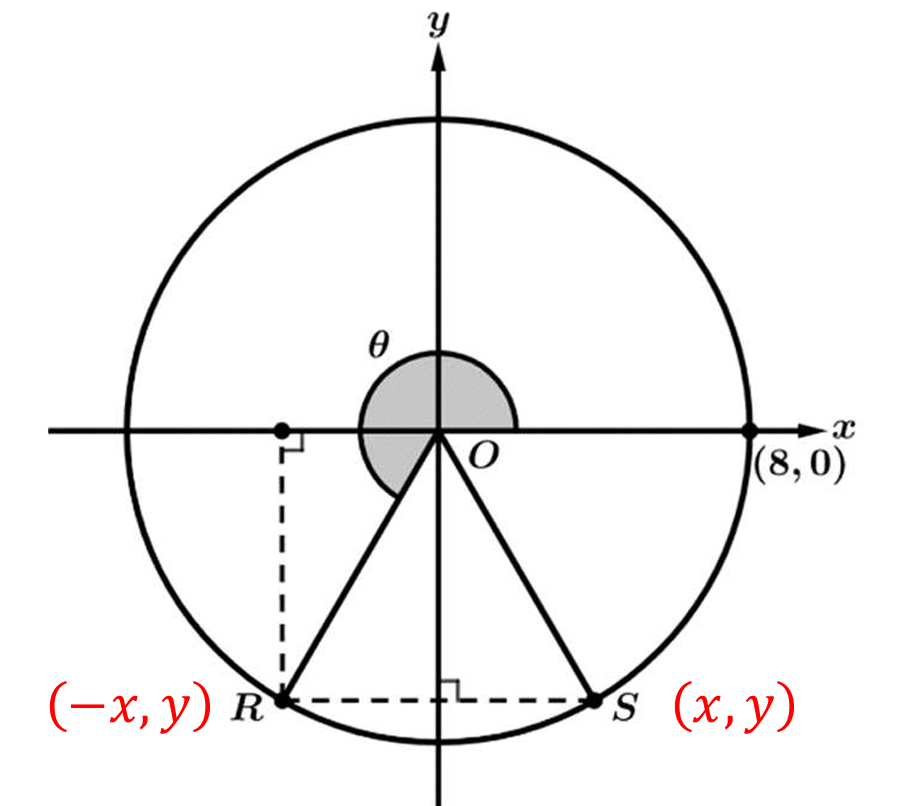
The circle intersects the positive x-axis at the point \((8, 0)\), indicating that the radius of the circle is \(r = 8\).
By definition, for any angle \(\theta\) in standard position, the cosine is the ratio of the x-coordinate of the point on the terminal ray to the radius (\(\cos \theta = \frac{X}{r}\)).
The terminal ray of angle \(\theta\) intersects the circle at point \(R\), which has the coordinates \((-x, y)\).
The x-coordinate of \(R\) is \(-x\), which represents the horizontal displacement of the point from the y-axis.
Substituting these values into the cosine definition gives \(\cos \theta = \frac{-x}{8}\).
Therefore, the correct statement is that \(\cos \theta = \frac{-x}{8}\) because it relates the horizontal displacement of \(R\) to the radius.
▶️ Answer/Explanation
Angles that are in standard position and share a terminal ray are called coterminal angles.
Two angles \(\alpha\) and \(\beta\) are coterminal if their difference is an integer multiple of \(2\pi\). That is, \(\alpha – \beta = 2\pi k\), where \(k\) is an integer.
Let’s check the difference for each option:
(A) \( -\frac{\pi}{2} – \frac{\pi}{2} = -\pi \) (Not a multiple of \(2\pi\))
(B) \( -\frac{\pi}{2} – (-\frac{3\pi}{2}) = \pi \) (Not a multiple of \(2\pi\))
(C) \( \frac{\pi}{2} – (-\frac{3\pi}{2}) = \frac{\pi}{2} + \frac{3\pi}{2} = \frac{4\pi}{2} = 2\pi \) (This is a multiple of \(2\pi\))
(D) \( \frac{\pi}{2} – \frac{3\pi}{2} = -\pi \) (Not a multiple of \(2\pi\))
Therefore, the angles in option (C) share the same terminal ray.
▶️ Answer/Explanation
The correct answer is (C).
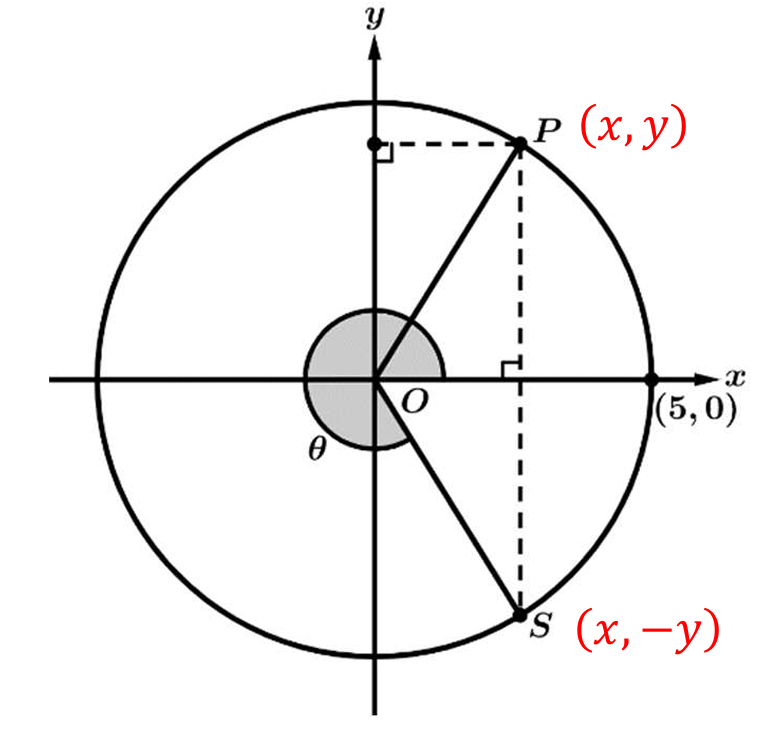
1. By definition, for any point \((X, Y)\) on the terminal ray of an angle \(\theta\) in standard position, \(\sin \theta = \frac{Y}{r}\), where \(r\) is the distance from the origin.
2. The terminal ray of angle \(\theta\) intersects the circle at point \(S\), which has the coordinates \((x, -y)\).
3. The circle intersects the positive \(x\)-axis at \((5,0)\), which implies the radius of the circle is \(r = 5\).
4. The vertical displacement of point \(S\) from the \(x\)-axis corresponds to its \(y\)-coordinate, which is \(-y\).
5. Substituting these values into the sine definition gives \(\sin \theta = \frac{-y}{5}\).
6. This matches option (C), which correctly identifies the ratio as the vertical displacement of \(S\) divided by the distance to the origin.
▶️ Answer/Explanation
Angles in standard position that share a terminal ray are called coterminal angles.
For two angles \(\alpha\) and \(\beta\) to be coterminal, their difference must be an integer multiple of a full rotation, \(2\pi\).
The condition is: \(\beta – \alpha = 2\pi k\), where \(k\) is an integer.
Check (A): \(\frac{7\pi}{6} – \frac{\pi}{6} = \pi\) (Not a multiple of \(2\pi\)).
Check (B): \(-\frac{5\pi}{3} – (-\frac{\pi}{3}) = -\frac{4\pi}{3}\) (Not a multiple of \(2\pi\)).
Check (C): \(\frac{\pi}{2} – (-\frac{\pi}{2}) = \pi\) (Not a multiple of \(2\pi\)).
Check (D): \(\frac{9\pi}{4} – \frac{\pi}{4} = \frac{8\pi}{4} = 2\pi\). This satisfies the condition with \(k=1\).
Therefore, option (D) is the correct answer.
▶️ Answer/Explanation
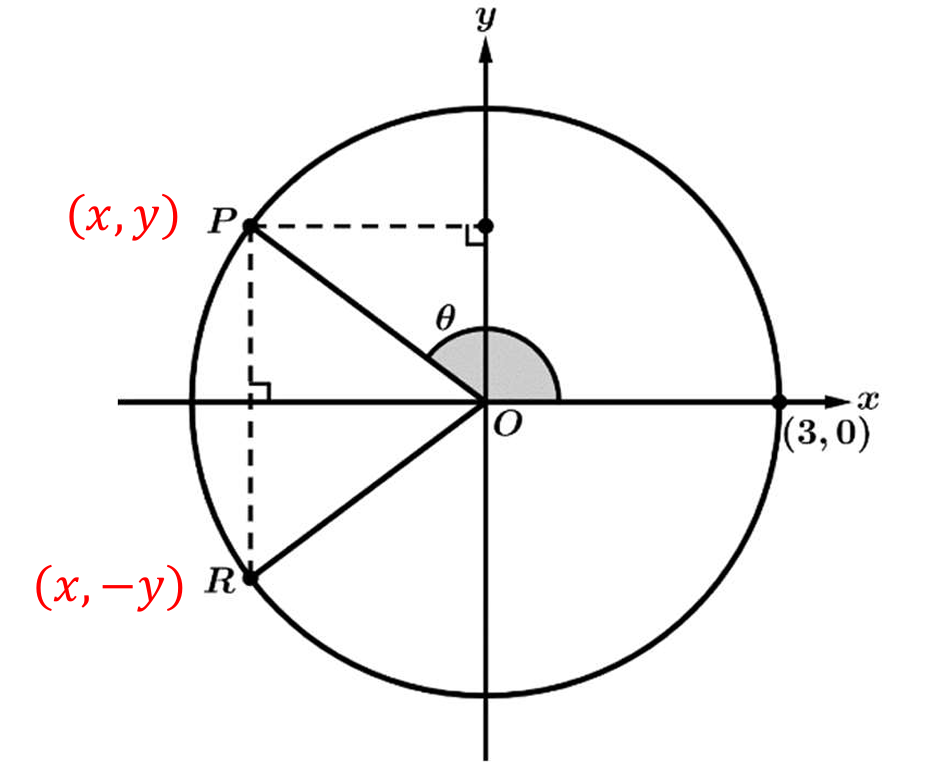
The tangent of an angle \(\theta\) in standard position is defined by the coordinates of a point on its terminal ray.
In this figure, the point \(P(x, y)\) lies specifically on the terminal ray of the angle \(\theta\).
By definition, \(\tan \theta = \frac{\text{ordinate}}{\text{abscissa}} = \frac{y}{x}\).
The coordinate \(y\) corresponds to the vertical displacement of the point \(P\) from the x-axis.
The coordinate \(x\) corresponds to the horizontal displacement of the point \(P\) from the y-axis (origin).
Therefore, \(\tan \theta\) is correctly described as the ratio of the vertical displacement of \(P\) to the horizontal displacement of \(P\).
Point \(R\) lies on a different ray (corresponding to angle \(-\theta\)), so its coordinates define \(\tan(-\theta)\), not \(\tan(\theta)\).
Thus, the correct statement corresponds to option (A).
▶️ Answer/Explanation
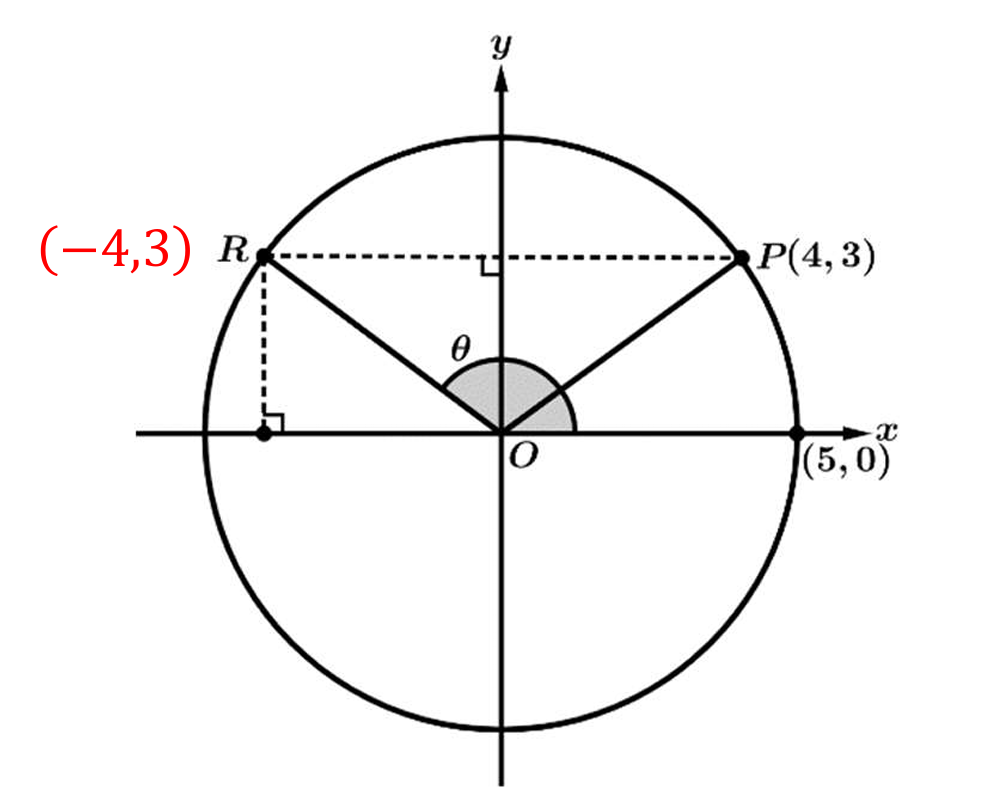
The dashed horizontal line connecting \(R\) and \(P\) indicates they have the same \(y\)-coordinate. Since \(P\) is \((4, 3)\), then \(y_R = 3\).
Point \(R\) lies on the circle defined by \(x^2 + y^2 = r^2\). With \(r=5\) and \(y=3\), we solve for \(x_R\).
\(x_R^2 + 3^2 = 5^2 \Rightarrow x_R^2 + 9 = 25 \Rightarrow x_R^2 = 16\).
Since \(R\) is in the second quadrant, its \(x\)-coordinate must be negative, so \(x_R = -4\). Thus, \(R = (-4, 3)\).
The definition of the tangent function for a point \((x, y)\) on the terminal ray is \(\tan \theta = \frac{y}{x}\).
Substituting the coordinates of \(R\): \(\tan \theta = \frac{3}{-4}\).
Therefore, \(\tan \theta = -\frac{3}{4}\).
Correct Option: (A)
▶️ Answer/Explanation
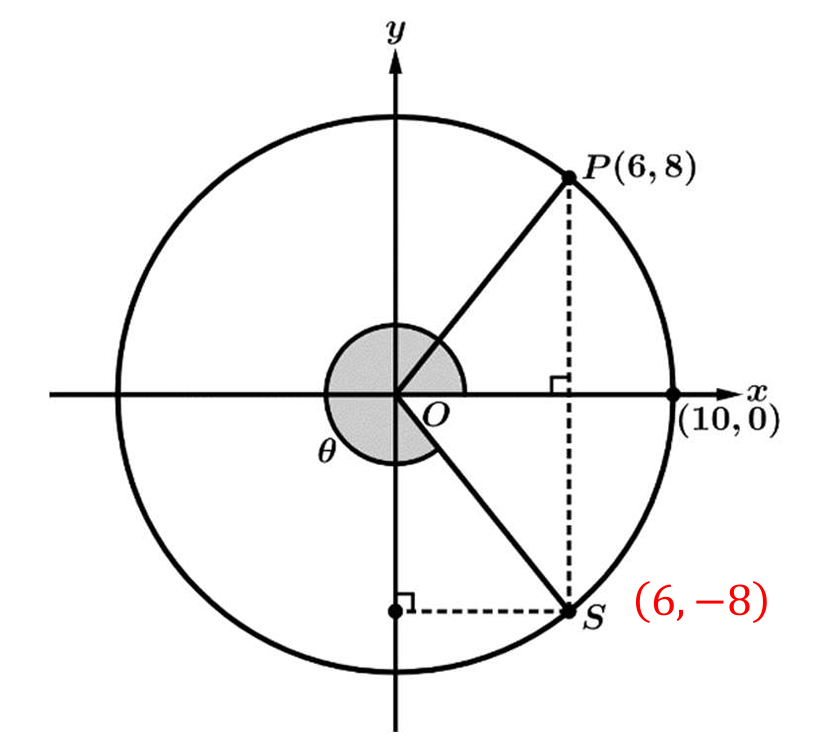
From the figure, point \( S \) shares the same x-coordinate as point \( P(6, 8) \), so \( x_S = 6 \).
Since \( S \) lies on the circle in the fourth quadrant, its y-coordinate is negative.
Using the circle equation \( x^2 + y^2 = r^2 \) with \( r=10 \), we get \( 6^2 + y^2 = 10^2 \), which yields \( y = -8 \).
The definition of sine for an angle in standard position is \( \sin \theta = \frac{y}{r} \).
Substituting the values for point \( S \): \( y = -8 \) and \( r = 10 \).
Thus, \( \sin \theta = \frac{-8}{10} = -\frac{4}{5} \).
Correct Option: (A)
▶️ Answer/Explanation
The correct option is (D).
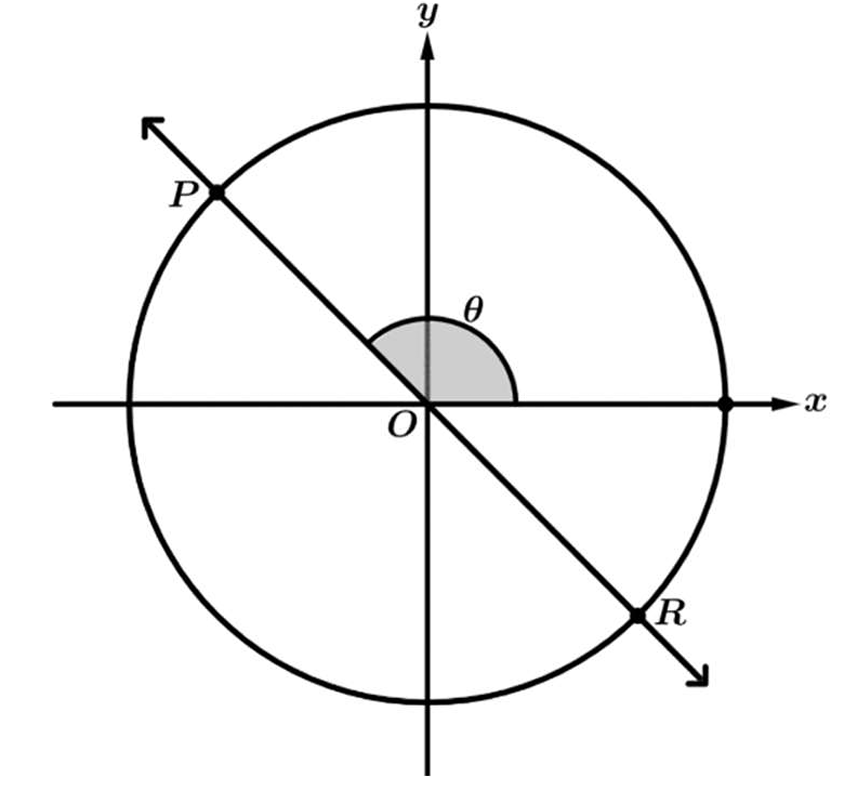
• The terminal ray of angle \(\theta\) lies on the line given by the equation \(y = -\frac{4}{3}x\).
• The slope of a line passing through the origin is given by \(m\) in the equation \(y = mx\). Here, the slope \(m = -\frac{4}{3}\).
• By definition, the tangent of an angle \(\theta\) in standard position is equal to the slope of its terminal ray.
• Therefore, \(\tan \theta = -\frac{4}{3}\).
• To check other values: Since the ray is in Quadrant II, let \(x = -3\) and \(y = 4\). The radius \(r = \sqrt{(-3)^2 + 4^2} = 5\).
• Calculating cosine: \(\cos \theta = \frac{x}{r} = -\frac{3}{5}\). This confirms options (A) and (B) are incorrect.
▶️ Answer/Explanation
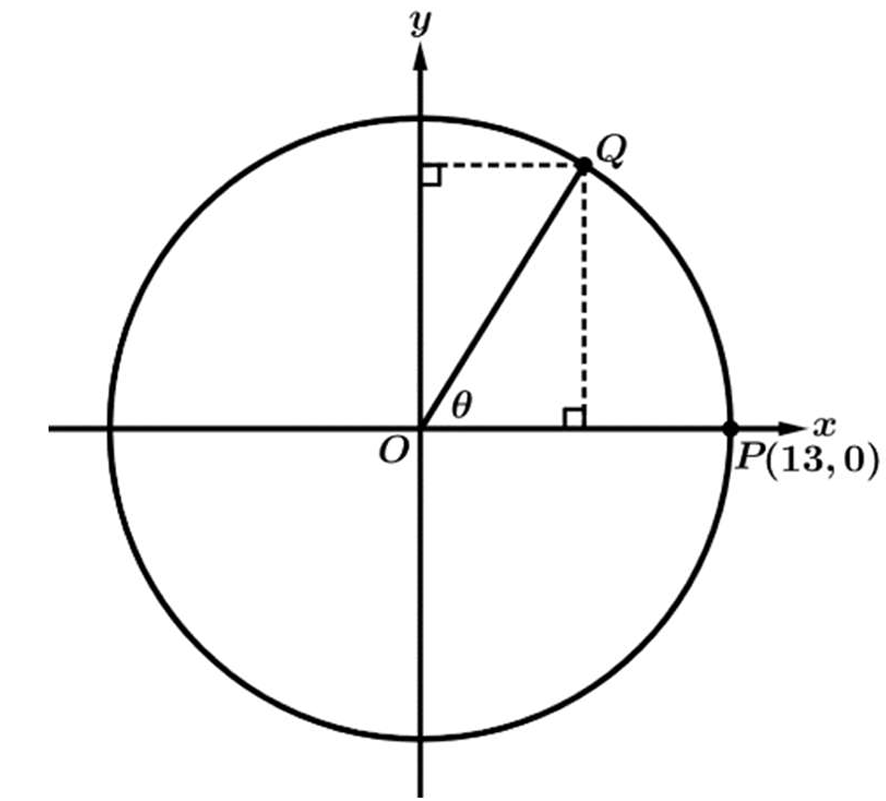
Step 1: Identify the radius of the circle. Since point \(P(13, 0)\) lies on the circle centered at the origin \((0,0)\), the radius is \(r = 13\).
Step 2: Calculate the angle \(\theta\). The length of the intercepted arc \(PQ\) is given as \(s = 15\). Using the formula \(s = r\theta\), we determine that \(\theta = \frac{s}{r} = \frac{15}{13}\) radians.
Step 3: Determine the coordinates of point \(Q\). For a circle with radius \(r\) and angle \(\theta\), the coordinates of a point on the circle are \((x, y) = (r\cos\theta, r\sin\theta)\).
Step 4: Find the distance from the \(x\)-axis. The distance of point \(Q\) from the \(x\)-axis is the vertical distance, which corresponds to the \(y\)-coordinate.
Step 5: Substitute the known values. The \(y\)-coordinate is \(13\sin(\theta)\). Substituting \(\theta = \frac{15}{13}\), we get \(13\sin\left(\frac{15}{13}\right)\), which matches option (D).
▶️ Answer/Explanation
The correct answer is (C).
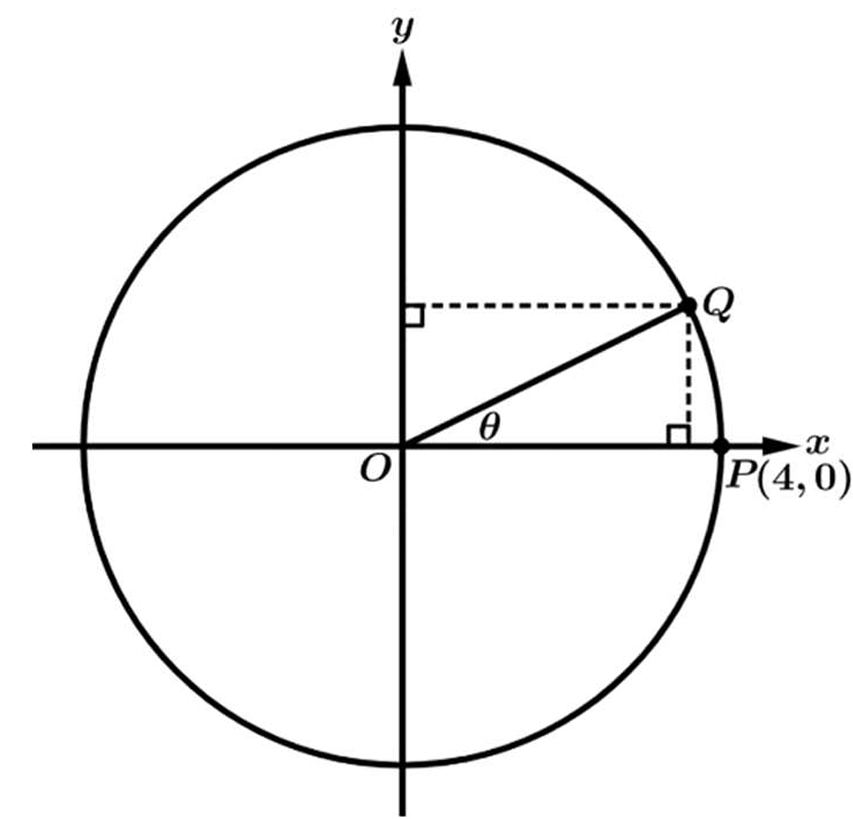
Since point \(P(4, 0)\) lies on the circle centered at the origin, the radius of the circle is \(r = 4\).
Using the arc length formula \(s = r\theta\), where \(s=3\) and \(r=4\), we find the angle: \(3 = 4\theta \Rightarrow \theta = \frac{3}{4}\) radians.
The coordinates of point \(Q\) on the circle are determined by \((x, y) = (r \cos \theta, r \sin \theta)\).
Substituting our values, the coordinates for \(Q\) become \(\left(4 \cos \left(\frac{3}{4}\right), 4 \sin \left(\frac{3}{4}\right)\right)\).
The distance of any point from the \(y\)-axis is represented by the absolute value of its \(x\)-coordinate.
Therefore, the distance of point \(Q\) from the \(y\)-axis is \(4 \cos\left(\frac{3}{4}\right)\).
▶️ Answer/Explanation
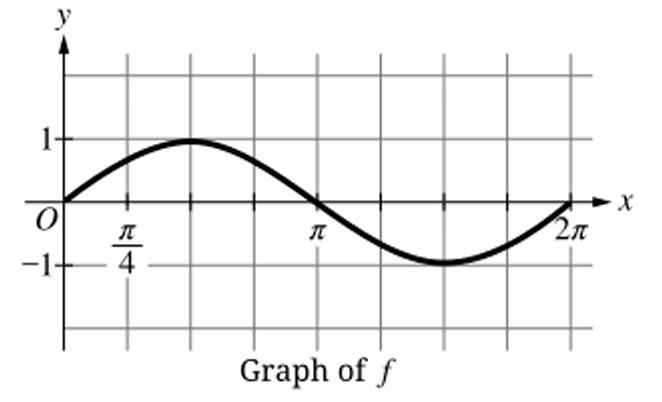
The graph starts at $(0,0)$ and follows the shape of $y = \sin(x)$.
On a unit circle, the coordinates of point $P$ are $(\cos\theta, \sin\theta)$.
The $y$-coordinate, $\sin\theta$, represents the vertical displacement from the $x$-axis.
“Displacement” is used instead of “distance” because the function $f$ has negative values.
Distance is always non-negative, whereas $f$ is negative on the interval $(\pi, 2\pi)$.
Therefore, $f$ represents the vertical displacement of $P$ for $0 \le \theta \le 2\pi$.
The correct option is (C).
▶️ Answer/Explanation
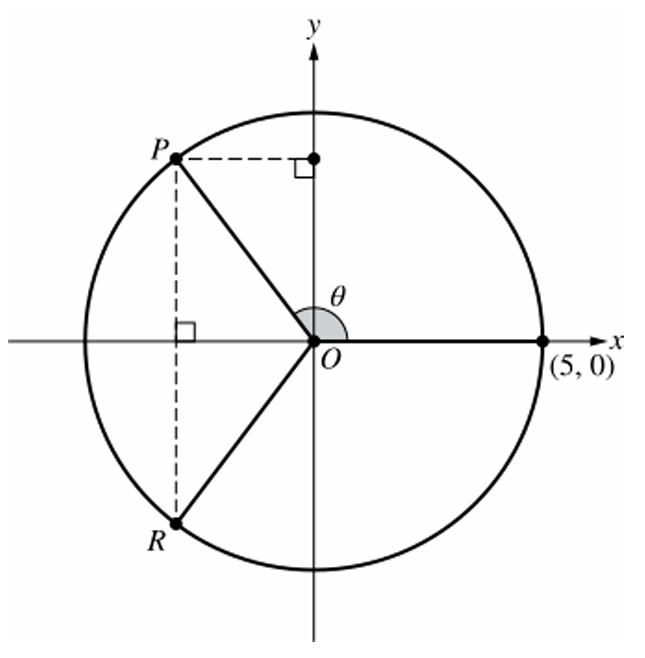
The circle is centered at the origin $(0, 0)$ and passes through $(5, 0)$, so its radius $r$ is $5$.
Point $P(x, y)$ lies on the terminal ray of the angle $\theta$ in standard position.
By trigonometric definition on a circle, $\sin \theta$ is the ratio of the $y$-coordinate to the radius: $\sin \theta = \frac{y}{r}$.
The $y$-coordinate represents the vertical displacement of point $P$ from the $x$-axis.
The radius $r = 5$ represents the distance from the origin to point $P$.
Therefore, $\sin \theta = \frac{y}{5}$ based on the position and coordinates of point $P$.
This matches option (D).
▶️ Answer/Explanation
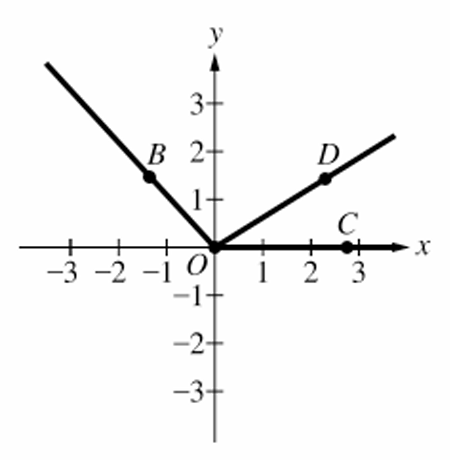
An angle is in standard position if its vertex is at the origin $(0,0)$ and its initial ray lies on the positive $x$-axis.
In the given figure, point $C$ lies on the positive $x$-axis at $(3,0)$, making ray $OC$ the initial ray.
Angle $COB$ starts at ray $OC$ and rotates counter-clockwise to terminal ray $OB$.
Therefore, angle $COB$ is in standard position with initial ray $OC$ and terminal ray $OB$.
Options (C) and (D) are incorrect because the initial ray for standard position must be $OC$, not $OB$ or $OD$.
Option (A) is incorrect because it swaps the definitions of the initial and terminal rays.
The correct statement is (B).
▶️ Answer/Explanation
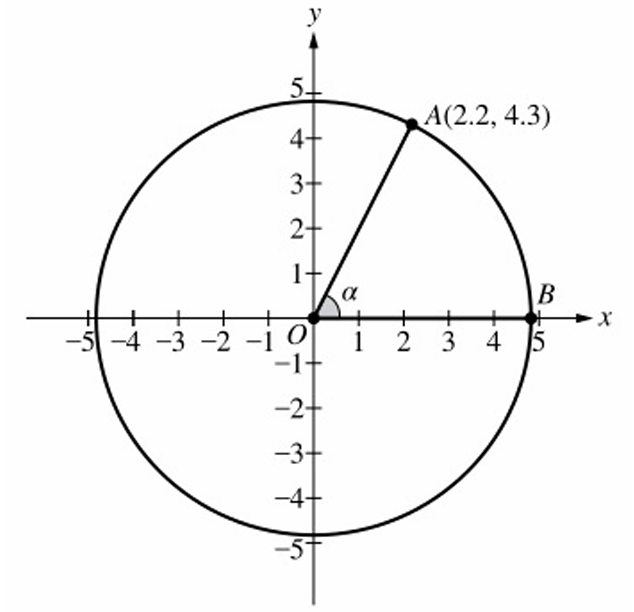
Point $A$ lies on the circle with coordinates $(x, y) = (2.2, 4.3)$.
The radius of the circle is given as $r = 4.8$.
For an angle $\alpha$ in standard position, the sine is defined as $\sin \alpha = \frac{y}{r}$.
Substitute the $y$-coordinate of point $A$, which is $4.3$.
Substitute the radius value, which is $4.8$.
Therefore, $\sin \alpha = \frac{4.3}{4.8}$.
The correct option is (B).
▶️ Answer/Explanation
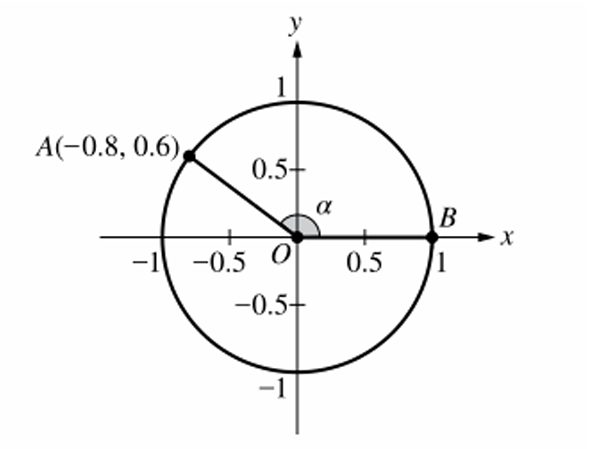
The terminal side of angle $\alpha$ intersects the unit circle at point $A(-0.8, 0.6)$.
By definition, for any point $(x, y)$ on a unit circle, $x = \cos \alpha$ and $y = \sin \alpha$.
The $x$-coordinate of point $A$ is given as $-0.8$.
Therefore, $\cos \alpha = -0.8$.
The correct option is (A).
▶️ Answer/Explanation
(A)(i) Rewrite \(g(x)\)
The function is given by \(g(x) = 3 \ln x – \frac{1}{2} \ln x\).
Combine the like terms:
\(g(x) = \left(3 – \frac{1}{2}\right) \ln x\)
\(g(x) = \frac{5}{2} \ln x\)
Apply the power property of logarithms, \(a \ln b = \ln(b^a)\):
\(g(x) = \ln\left(x^{5/2}\right)\)
(A)(ii) Rewrite \(h(x)\)
The function is given by \(h(x) = \frac{\sin^2 x – 1}{\cos x}\).
Recall the Pythagorean identity: \(\sin^2 x + \cos^2 x = 1\).
Rearrange the identity to isolate the numerator expression: \(\sin^2 x – 1 = -\cos^2 x\).
Substitute this into the function:
\(h(x) = \frac{-\cos^2 x}{\cos x}\)
Simplify the expression by canceling one \(\cos x\) term:
\(h(x) = -\cos x\)
(B)(i) Solve \(j(x) = 0\)
Set the function equal to zero: \(2(\sin x)(\cos x) = 0\).
Divide both sides by 2:
\(\sin x \cos x = 0\)
By the zero product property, either \(\sin x = 0\) or \(\cos x = 0\).
Case 1: \(\sin x = 0\). In the interval \(\left[0, \frac{\pi}{2}\right]\), \(x = 0\).
Case 2: \(\cos x = 0\). In the interval \(\left[0, \frac{\pi}{2}\right]\), \(x = \frac{\pi}{2}\).
The solutions are \(x = 0\) and \(x = \frac{\pi}{2}\).
(B)(ii) Solve \(k(x) = 3e\)
Set the function equal to \(3e\):
\(8e^{(3x)} – e = 3e\)
Add \(e\) to both sides:
\(8e^{(3x)} = 4e\)
Divide both sides by 8:
\(e^{(3x)} = \frac{4e}{8}\)
\(e^{(3x)} = \frac{e}{2}\)
Take the natural logarithm (\(\ln\)) of both sides:
\(\ln\left(e^{3x}\right) = \ln\left(\frac{e}{2}\right)\)
Use logarithm properties to simplify (\(\ln(e^a) = a\) and \(\ln(a/b) = \ln a – \ln b\)):
\(3x = \ln e – \ln 2\)
Since \(\ln e = 1\):
\(3x = 1 – \ln 2\)
Divide by 3:
\(x = \frac{1 – \ln 2}{3}\)
(C) Find input values for \(m(x) = \frac{9}{2}\)
Set the function equal to \(\frac{9}{2}\):
\(\cos(2x) + 4 = \frac{9}{2}\)
Subtract 4 from both sides (note that \(4 = \frac{8}{2}\)):
\(\cos(2x) = \frac{9}{2} – \frac{8}{2}\)
\(\cos(2x) = \frac{1}{2}\)
The reference angle for cosine equal to \(\frac{1}{2}\) is \(\frac{\pi}{3}\).
The general solution for \(2x\) is:
\(2x = \frac{\pi}{3} + 2\pi n\) or \(2x = -\frac{\pi}{3} + 2\pi n\) (where \(n\) is an integer).
Solve for \(x\) by dividing by 2:
\(x = \frac{\pi}{6} + \pi n\) or \(x = -\frac{\pi}{6} + \pi n\)
Combining these, the input values are \(x = \pm \frac{\pi}{6} + \pi n\) for any integer \(n\).