AP Precalculus -3.2 Sine, Cosine, and Tangent- Study Notes - Effective Fall 2023
AP Precalculus -3.2 Sine, Cosine, and Tangent- Study Notes – Effective Fall 2023
AP Precalculus -3.2 Sine, Cosine, and Tangent- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine the sine, cosine, and tangent of an angle using the unit circle.
Key Concepts:
Angles in Standard Position
Radian Measure of an Angle
Sine of an Angle Using the Unit Circle
Cosine of an Angle Using the Unit Circle
Tangent of an Angle Using the Unit Circle
Angles in Standard Position
In the coordinate plane, an angle is said to be in standard position when its vertex is located at the origin and one of its rays lies along the positive x-axis.
The ray that lies on the positive x-axis is called the initial ray. The other ray is called the terminal ray.
Direction of Rotation
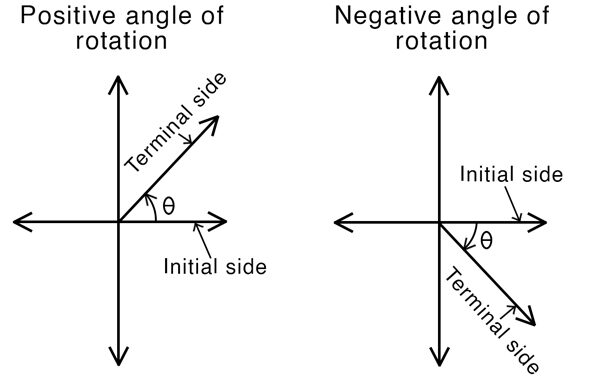
A positive angle measure corresponds to a counterclockwise rotation from the positive x-axis.
A negative angle measure corresponds to a clockwise rotation from the positive x-axis.
Coterminal Angles
Angles in standard position that share the same terminal ray are called coterminal angles.
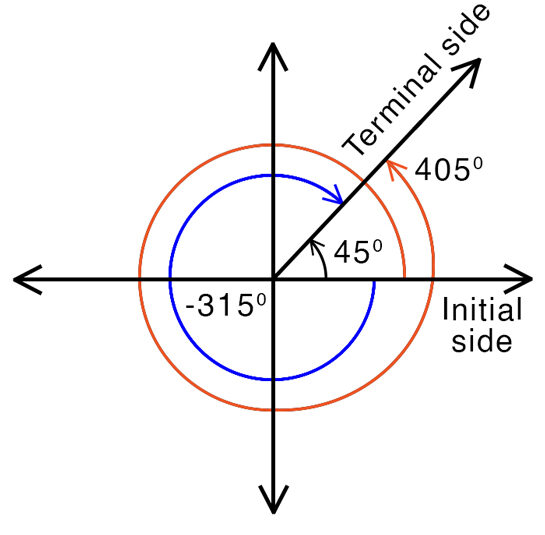
Coterminal angles differ by an integer number of full revolutions.
\( \theta + 360k \) degrees or \( \theta + 2\pi k \) radians, where \( k \) is an integer
Example:
Describe the angle \( 120^\circ \) in standard position and give one positive and one negative coterminal angle.
▶️ Answer/Explanation
The angle \( 120^\circ \) is measured counterclockwise from the positive x-axis, so it is a positive angle in standard position.
A positive coterminal angle is:
\( 120 + 360 = 480^\circ \)
A negative coterminal angle is:
\( 120 – 360 = -240^\circ \)
All three angles share the same terminal ray.
Example:
Determine whether the angles \( -\frac{\pi}{3} \) and \( \frac{5\pi}{3} \) are coterminal.
▶️ Answer/Explanation
Two angles are coterminal if their difference is an integer multiple of \( 2\pi \).
Compute the difference:
\( \frac{5\pi}{3} – \left(-\frac{\pi}{3}\right) = \frac{6\pi}{3} = 2\pi \)
Since the difference is \( 2\pi \), the angles differ by one full revolution.
Conclusion: The angles are coterminal and share the same terminal ray.
Radian Measure of an Angle
The radian measure of an angle in standard position is defined using a circle centered at the origin.
Specifically, the radian measure of an angle is the ratio of the length of the arc subtended by the angle to the radius of the circle.
\( \text{Radian measure} = \dfrac{\text{arc length}}{\text{radius}} \)
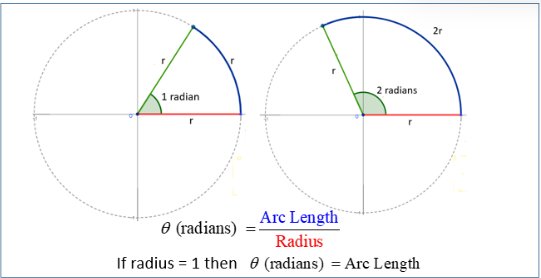
If the circle has radius \( r \) and the arc length is \( s \), then the radian measure \( \theta \) is
\( \theta = \dfrac{s}{r} \)
Unit Circle Interpretation
A unit circle is a circle with radius 1.
On the unit circle, the radian measure of an angle is numerically equal to the length of the arc it subtends.
If \( r = 1 \), then \( \theta = s \)
This makes radians especially useful for studying trigonometric and periodic functions.
Example:
An angle in standard position subtends an arc of length 5 units on a circle with radius 2 units. Find the radian measure of the angle.
▶️ Answer/Explanation
Use the radian formula:
\( \theta = \dfrac{s}{r} \)
Substitute \( s = 5 \) and \( r = 2 \):
\( \theta = \dfrac{5}{2} \)
Final answer: The radian measure is \( \dfrac{5}{2} \) radians.
Example:
An angle subtends an arc of length \( \pi \) on the unit circle. Find the radian measure of the angle.
▶️ Answer/Explanation
On the unit circle, the radius is 1.
Using \( \theta = \dfrac{s}{r} \):
\( \theta = \dfrac{\pi}{1} = \pi \)
Final answer: The radian measure of the angle is \( \pi \) radians.
Sine of an Angle Using the Unit Circle
Consider an angle \( \theta \) in standard position and a circle centered at the origin.
The terminal ray of the angle intersects the circle at a point \( P \).
The sine of the angle is defined as the ratio of the vertical displacement of point \( P \) from the x-axis to the distance from the origin to point \( P \).
\( \sin \theta = \dfrac{\text{vertical displacement of } P}{\text{distance from origin to } P} \)
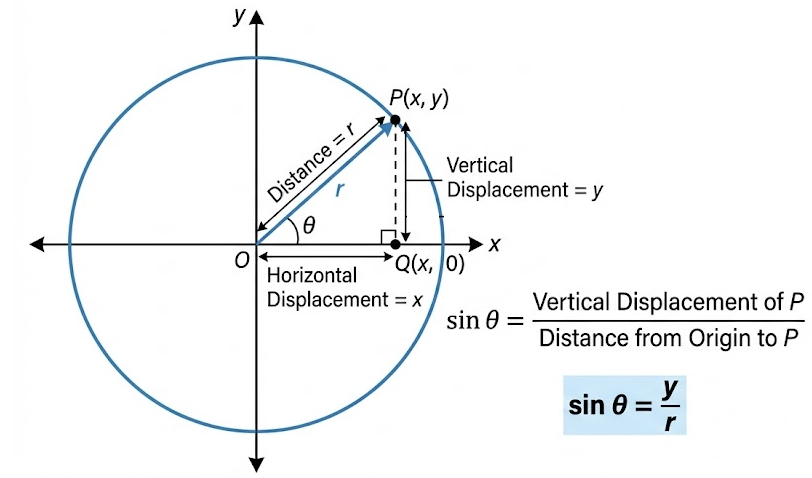
If the circle has radius \( r \), then the distance from the origin to point \( P \) is \( r \).
Unit Circle Interpretation
On the unit circle, the radius is 1.
Therefore, for a unit circle, the sine of an angle is simply the y-coordinate of point \( P \).
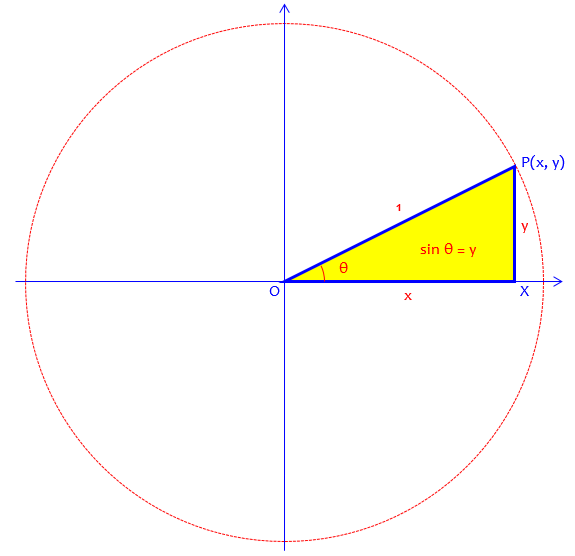
If \( P = (x, y) \), then \( \sin \theta = y \)
This definition allows sine values to be interpreted directly from the coordinate plane.
Example:
An angle \( \theta \) in standard position intersects the unit circle at the point \( P = \left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right) \). Find \( \sin \theta \).
▶️ Answer/Explanation
On the unit circle, the sine of the angle equals the y-coordinate of point \( P \).
\( \sin \theta = \dfrac{\sqrt{3}}{2} \)
Final answer: \( \sin \theta = \dfrac{\sqrt{3}}{2} \).
Example:
An angle \( \theta \) intersects a circle of radius 5 at a point \( P \) with vertical displacement 3 units above the x-axis. Find \( \sin \theta \).
▶️ Answer/Explanation
Use the sine definition:
\( \sin \theta = \dfrac{\text{vertical displacement}}{\text{distance from origin}} \)
Substitute the given values:
\( \sin \theta = \dfrac{3}{5} \)
Final answer: \( \sin \theta = \dfrac{3}{5} \).
Cosine of an Angle Using the Unit Circle
Consider an angle \( \theta \) in standard position and a circle centered at the origin.
The terminal ray of the angle intersects the circle at a point \( P \).
The cosine of the angle is defined as the ratio of the horizontal displacement of point \( P \) from the y-axis to the distance from the origin to point \( P \).
\( \cos \theta = \dfrac{\text{horizontal displacement of } P}{\text{distance from origin to } P} \)
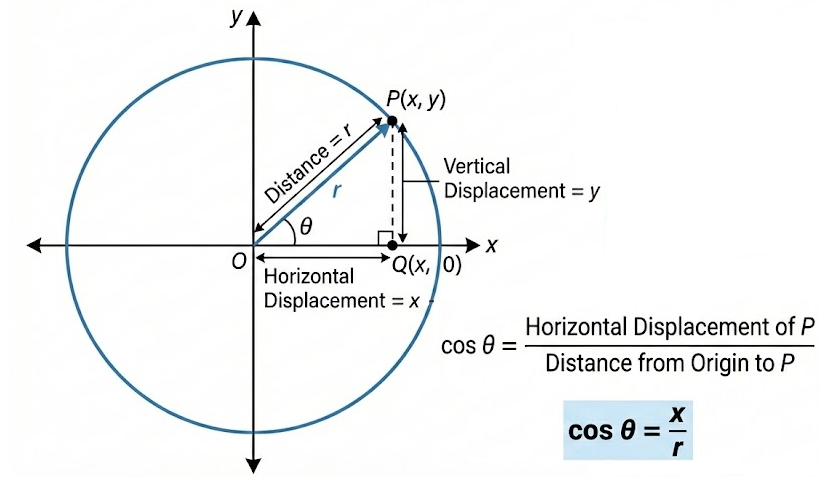
If the circle has radius \( r \), then the distance from the origin to point \( P \) is \( r \).
Unit Circle Interpretation
On the unit circle, the radius is 1.
Therefore, for a unit circle, the cosine of an angle is simply the x-coordinate of point \( P \).
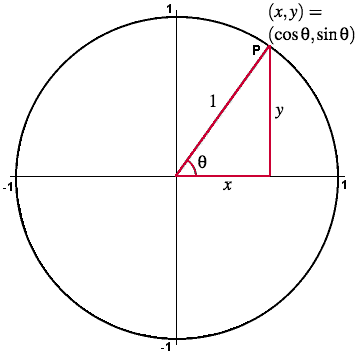
If \( P = (x, y) \), then \( \cos \theta = x \)
This definition allows cosine values to be interpreted directly from the coordinate plane.
Example:
An angle \( \theta \) in standard position intersects the unit circle at the point \( P = \left(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}\right) \). Find \( \cos \theta \).
▶️ Answer/Explanation
On the unit circle, the cosine of the angle equals the x-coordinate of point \( P \).
\( \cos \theta = -\dfrac{\sqrt{2}}{2} \)
Final answer: \( \cos \theta = -\dfrac{\sqrt{2}}{2} \).
Example:
An angle \( \theta \) intersects a circle of radius 10 at a point \( P \) with a horizontal displacement of 6 units to the right of the y-axis. Find \( \cos \theta \).
▶️ Answer/Explanation
Use the cosine definition:
\( \cos \theta = \dfrac{\text{horizontal displacement}}{\text{distance from origin}} \)
Substitute the given values:
\( \cos \theta = \dfrac{6}{10} = \dfrac{3}{5} \)
Final answer: \( \cos \theta = \dfrac{3}{5} \).
Tangent of an Angle Using the Unit Circle
Consider an angle \( \theta \) in standard position.
The tangent of the angle is defined as the slope of the terminal ray, provided that the slope exists.
Since slope is the ratio of vertical change to horizontal change, the tangent of an angle can be written as
\( \tan \theta = \dfrac{\text{vertical displacement}}{\text{horizontal displacement}} \)
When the terminal ray intersects the unit circle at a point \( P = (x, y) \), the vertical displacement is \( y \) and the horizontal displacement is \( x \).
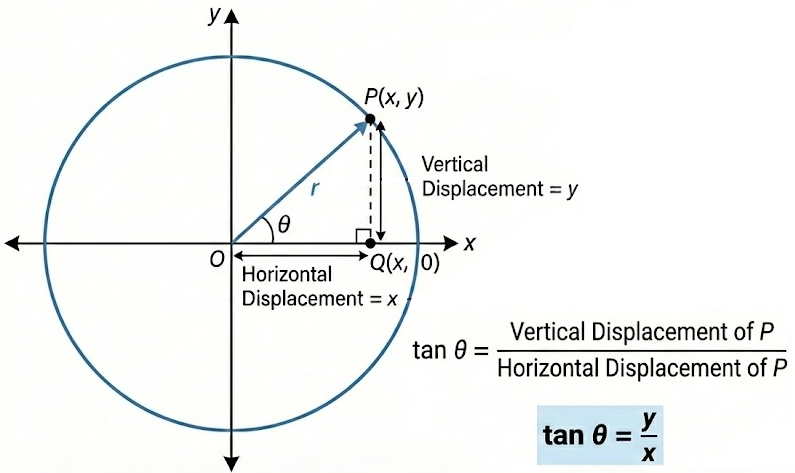
Therefore,
\( \tan \theta = \dfrac{y}{x} \), provided \( x \ne 0 \)
Relationship with Sine and Cosine
Since on the unit circle \( \sin \theta = y \) and \( \cos \theta = x \), the tangent can also be written as
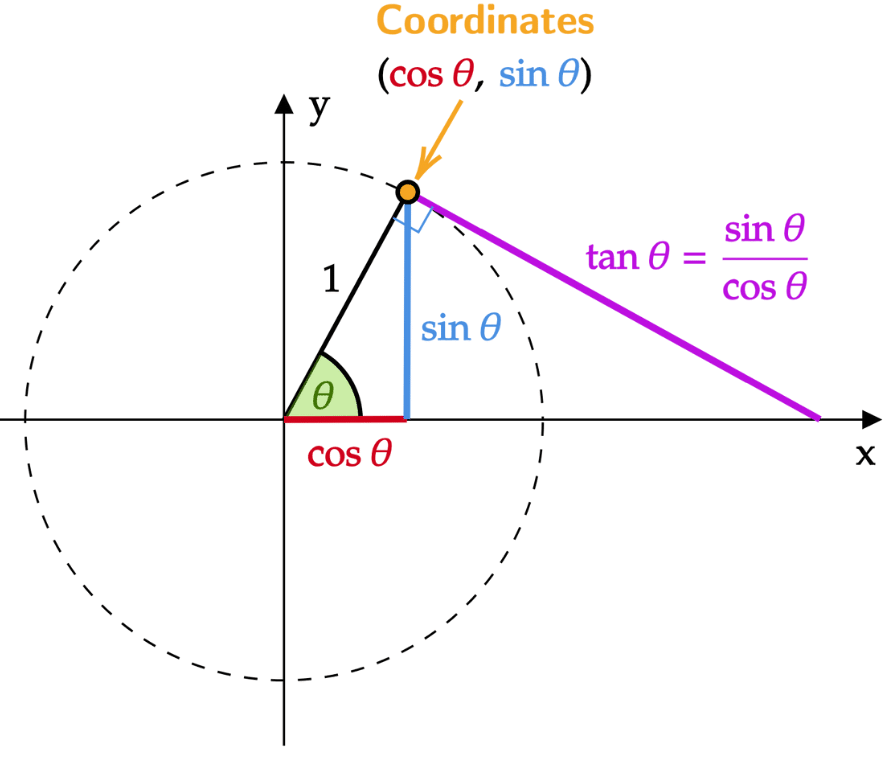
\( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \), provided \( \cos \theta \ne 0 \)
If the terminal ray is vertical, the tangent is undefined because the slope does not exist.
Example:
An angle \( \theta \) in standard position intersects the unit circle at the point \( P = \left(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}\right) \). Find \( \tan \theta \).
▶️ Answer/Explanation
Use the unit circle definition of tangent.
\( \tan \theta = \dfrac{y}{x} \)
Substitute the coordinates of point \( P \):
\( \tan \theta = \dfrac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \dfrac{1}{\sqrt{3}} \)
Final answer: \( \tan \theta = \dfrac{1}{\sqrt{3}} \).
Example:
Find \( \tan \theta \) if \( \sin \theta = -\dfrac{3}{5} \) and \( \cos \theta = \dfrac{4}{5} \).
▶️ Answer/Explanation
Use the identity \( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \).
\( \tan \theta = \dfrac{-\frac{3}{5}}{\frac{4}{5}} \)
Simplify:
\( \tan \theta = -\dfrac{3}{4} \)
Final answer: \( \tan \theta = -\dfrac{3}{4} \).
