AP Precalculus -3.3 Sine and Cosine Values- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.3 Sine and Cosine Values- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.3 Sine and Cosine Values- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

In the $ xy $-plane, the terminal ray of angle $ \theta $ in standard position intersects a circle of radius $ r $ at the point $ \left( 10, -10\sqrt{3} \right) $. What are the values of $ \theta $ and $ r $?

(A) $ \theta = \frac{5\pi}{3} $ and $ r = 10 $
(B) $ \theta = \frac{5\pi}{3} $ and $ r = 20 $
(C) $ \theta = \frac{11\pi}{6} $ and $ r = 10 $
(D) $ \theta = \frac{11\pi}{6} $ and $ r = 20 $

▶️ Answer/Explanation

Detailed solution

We have $ x = 10, y = -10\sqrt{3} $.
The ratio $ \frac{y}{x} = -\sqrt{3} $, so $ \tan\theta = -\sqrt{3} $.
In Quadrant IV, $ \theta = \frac{5\pi}{3} $ (since $\tan\frac{5\pi}{3} = -\sqrt{3}$).
Check: $ \cos\frac{5\pi}{3} = \frac12 $, $ \sin\frac{5\pi}{3} = -\frac{\sqrt{3}}{2} $.
Now, $ r\cos\theta = r \cdot \frac12 = 10 $ → $ r = 20 $.
Verify: $ r\sin\theta = 20 \cdot \left(-\frac{\sqrt{3}}{2}\right) = -10\sqrt{3} $,
Thus $ \theta = \frac{5\pi}{3} $ and $ r = 20 $.
✅ Answer: (B)

Question

The figure shows the terminal ray of angle $\theta$, in standard position, intersecting the unit circle at point $P$ in the $xy$-plane. The function $g$ is given by $g(z) = \cos z$. For the angle $\omega$ (not shown), $\theta < \omega < \pi$. Which of the following is true?

(A) $g(\omega) < g(\theta)$
(B) $g(\omega) > g(\theta)$
(C) $g(\omega) = g(\theta)$
(D) Depending on the value of $\omega$, sometimes $g(\omega) < g(\theta)$ and sometimes $g(\omega) > g(\theta)$.

▶️ Answer/Explanation

Detailed solution

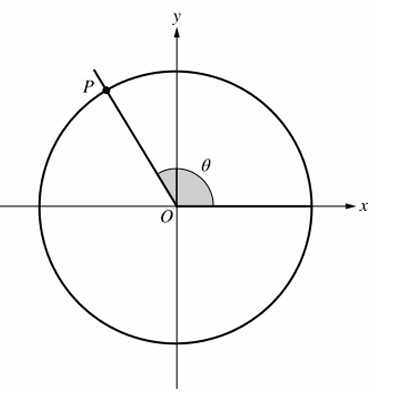
On the unit circle, $ \cos z $ gives the $ x $-coordinate.
From the diagram, $ \theta $ is in Quadrant I ($ 0 < \theta < \frac{\pi}{2} $) since $ P $ is in Quadrant I.
If $ \theta < \omega < \pi $, then $ \omega $ is in Quadrant II.
Cosine decreases from 1 to -1 as the angle goes from 0 to $ \pi $, so for $ \omega > \theta $, $ \cos\omega < \cos\theta $.
Thus $ g(\omega) < g(\theta) $.
✅ Answer: (A)

Question

The figure shows the terminal ray of angle $\theta$, in standard position, intersecting the unit circle at point $P$ in the $xy$-plane. The function $f$ is given by $f(z) = \sin z$. For the angle $\beta$ (not shown), $\frac{\pi}{2} < \beta < \theta$. Which of the following is true?

(A) $f(\beta) < f(\theta)$
(B) $f(\beta) > f(\theta)$
(C) $f(\beta) = f(\theta)$
(D) Depending on the value of $\beta$, sometimes $f(\beta) < f(\theta)$ and sometimes $f(\beta) > f(\theta)$.

▶️ Answer/Explanation

Detailed solution

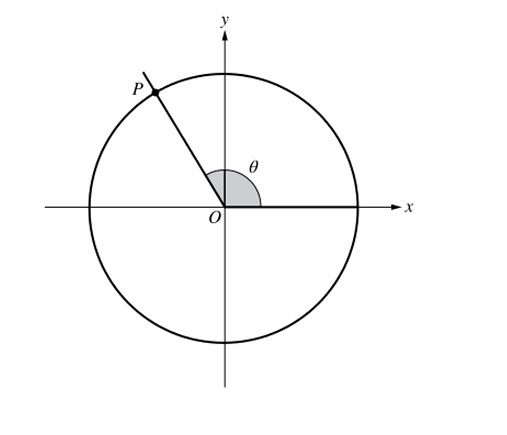
From the diagram, $ \theta $ is in Quadrant I and $ \theta > \frac{\pi}{2} $ ? Actually given $ \frac{\pi}{2} < \beta < \theta $, so $ \theta $ is > $ \frac{\pi}{2} $ as well, but since $ \theta $ is in Quadrant II from the figure (based on answer key reasoning). In Quadrant II, sine decreases as angle increases toward $ \pi $.
If $ \frac{\pi}{2} < \beta < \theta $, then $ \beta $ is closer to $ \frac{\pi}{2} $ where sine = 1, and $ \theta $ is farther from $ \frac{\pi}{2} $ so sine is smaller. Thus $ \sin\beta > \sin\theta $, so $ f(\beta) > f(\theta) $.
✅ Answer: (B)

Question

The figure shows equilateral triangle $ ABO $ with sides of length 10 in the $ xy $-plane. Segment $ AB $ is perpendicular to the $ x $-axis. The terminal ray of an angle $ \theta $ (not shown) in standard position passes through the point $ B $. What is the value of $ 10 \sin \theta $?

(A) $-5\sqrt{3}$
(B) $-\frac{\sqrt{3}}{2}$
(C) $\frac{1}{2}$
(D) 5

▶️ Answer/Explanation

Detailed solution

Step 1: Geometry of the triangle

Triangle $ABO$ is equilateral with side length $10$.
Hence,
$OA = OB = AB = 10$
and
$\angle AOB = 60^\circ.$

Step 2: Orientation in the coordinate plane

Segment $AB$ is perpendicular to the $x$-axis, so $A$ and $B$ have the same
$x$-coordinate and are symmetric about the $x$-axis.
Thus, the bisector of $\angle AOB$ lies along the negative $x$-axis.

Step 3: Determine the angle $\theta$

Since $\angle AOB = 60^\circ$, the ray $OB$ makes an angle of
$\theta = 180^\circ – 30^\circ = 150^\circ$
with the positive $x$-axis.

Step 4: Compute $10\sin\theta$

$\sin 150^\circ = \frac{1}{2}$

$10\sin\theta = 10 \cdot \frac{1}{2} = 5$

$\boxed{5}$

\textbf{Correct answer: (D)}

Question

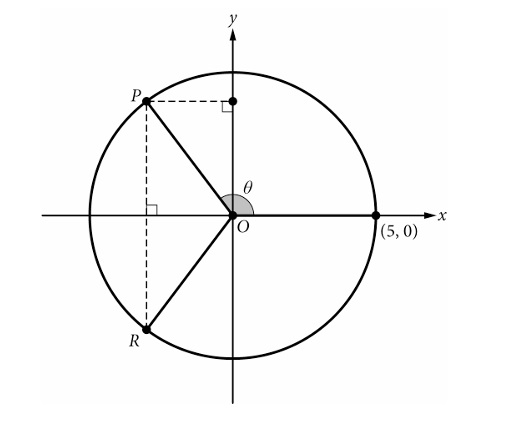
A circle centered at origin with radius 5 is shown. Point $P = (x, y)$ is on terminal ray of angle $\theta$, point $R = (x, -y)$. Which is true about $\sin\theta$?

(A) $ \sin\theta = \frac{x}{5} $, ratio of horizontal displacement of $P$ to distance from origin
(B) $ \sin\theta = \frac{x}{5} $, ratio of horizontal displacement of $R$ to distance from origin
(C) $ \sin\theta = -\frac{y}{5} $, ratio of vertical displacement of $R$ to distance from origin
(D) $ \sin\theta = \frac{y}{5} $, ratio of vertical displacement of $P$ to distance from origin

▶️ Answer/Explanation

Detailed solution

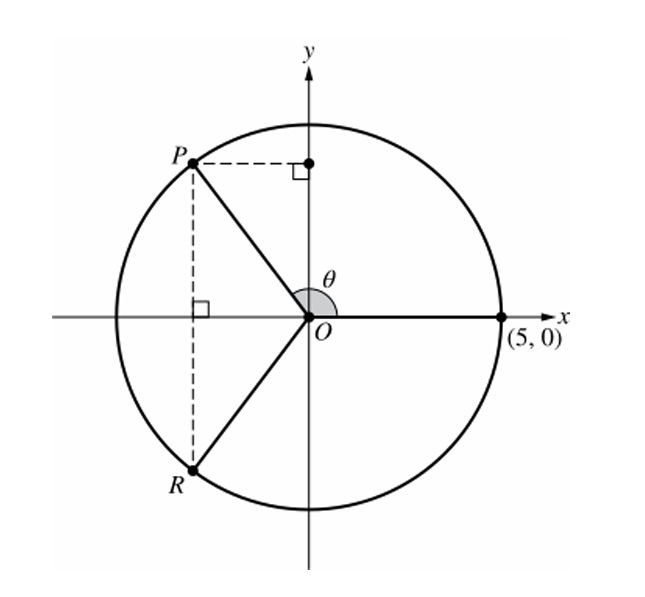
By definition on the unit circle (scaled by radius 5):
$ \sin\theta = \frac{\text{vertical displacement of }P}{ \text{distance from origin}} = \frac{y}{5} $.
✅ Answer: (D)

Question

The function $ f(x) = \sin(x + \frac{4\pi}{3}) $. What is $ f\left(\frac{3\pi}{4}\right) $?

(A) $ -\frac{\sqrt{6} – \sqrt{2}}{4} $
(B) $ \frac{\sqrt{2} + \sqrt{6}}{4} $
(C) $ \frac{\sqrt{2} – \sqrt{6}}{4} $
(D) $ \frac{\sqrt{6} – \sqrt{2}}{4} $

▶️ Answer/Explanation

Detailed solution

Use sum identity: $ \sin\left(\frac{3\pi}{4} + \frac{4\pi}{3}\right) = \sin\frac{3\pi}{4}\cos\frac{4\pi}{3} + \cos\frac{3\pi}{4}\sin\frac{4\pi}{3} $.
$ \sin\frac{3\pi}{4} = \frac{\sqrt{2}}{2} $, $ \cos\frac{4\pi}{3} = -\frac{1}{2} $, $ \cos\frac{3\pi}{4} = -\frac{\sqrt{2}}{2} $, $ \sin\frac{4\pi}{3} = -\frac{\sqrt{3}}{2} $.
Compute: $ \frac{\sqrt{2}}{2} \cdot -\frac{1}{2} + \left(-\frac{\sqrt{2}}{2}\right)\left(-\frac{\sqrt{3}}{2}\right) = -\frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} = \frac{\sqrt{6} – \sqrt{2}}{4} $.
✅ Answer: (D)

Question

A circle of radius 4.8 centered at origin has angle $ \alpha $ in standard position intersecting the circle at a point. Which is the value of $ \sin\alpha $?

(A) $ \frac{2.2}{4.8} $
(B) $ \frac{4.3}{4.8} $
(C) 2.2
(D) 4.3

▶️ Answer/Explanation

Detailed solution

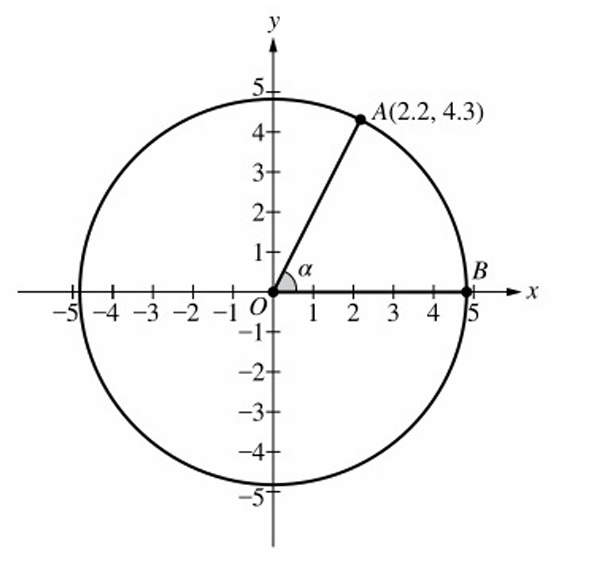
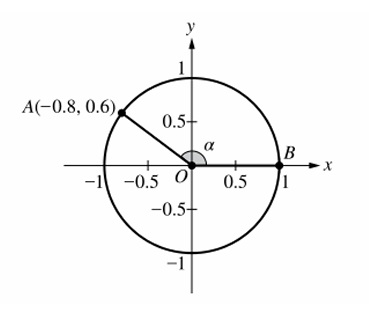
Sine is vertical displacement / radius.
From the figure (described in PDF), the vertical coordinate is 4.3.
Thus $ \sin\alpha = \frac{4.3}{4.8} $.
✅ Answer: (B)

Question

Unit circle with point $A(-0.8, 0.6)$ on terminal ray of angle $ \alpha $. What is $ \cos\alpha $?

(A) $-0.8$
(B) $-0.6$
(C) $0.6$
(D) $0.8$

▶️ Answer/Explanation

Detailed solution

On unit circle, $ \cos\alpha $ = $x$-coordinate of intersection point = $-0.8$.
✅ Answer: (A)

Question

The figure shows a circle centered at the origin with an angle of measure $\theta$ radians in standard position. The terminal ray of the angle intersects the circle at point $P$, and point $R$ also lies on the circle. The coordinates of $P$ are $(x, y)$, and the coordinates of $R$ are $(x, -y)$. Which of the following is true about the sine of $\theta$?

(A) $\sin \theta = \frac{x}{5}$, because it is the ratio of the horizontal displacement of $P$ from the $y$-axis to the distance between the origin and $P$.
(B) $\sin \theta = \frac{x}{5}$, because it is the ratio of the horizontal displacement of $R$ from the $y$-axis to the distance between the origin and $R$.
(C) $\sin \theta = -\frac{y}{5}$, because it is the ratio of the vertical displacement of $R$ from the $x$-axis to the distance between the origin and $R$.
(D) $\sin \theta = \frac{y}{5}$, because it is the ratio of the vertical displacement of $P$ from the $x$-axis to the distance between the origin and $P$.

▶️ Answer/Explanation

Detailed solution

Point $P$ is on the terminal ray of angle $\theta$. By definition, for a circle centered at the origin with radius $r$ (in the figure, radius = 5),
\[ \sin \theta = \frac{\text{vertical displacement of }P}{r} = \frac{y}{5} \]
Horizontal displacement gives cosine, not sine. $R$ is symmetric across the x-axis, so its vertical displacement is $-y$, giving $\sin(-\theta) = -\frac{y}{5}$, not $\sin \theta$.
Thus correct statement is: $\sin \theta = \frac{y}{5}$, because it’s the ratio of the vertical displacement of $P$ from the x-axis to the distance between the origin and $P$.
✅ Answer: (D)

Question

The figure above shows a circle of radius 5 along with the equilateral triangle $PQO$ . Which of the following gives the coordinates of point $P$?

(A) $\left( 5 \cos \frac{5\pi}{6}, 5 \sin \frac{5\pi}{6} \right)$

(B) $\left( 5 \cos \frac{\pi}{3}, 5 \sin \frac{\pi}{3} \right)$

(D) $\left( 5 \cos \frac{4\pi}{3}, 5 \sin \frac{4\pi}{3} \right)$

▶️ Answer/Explanation

Detailed solution

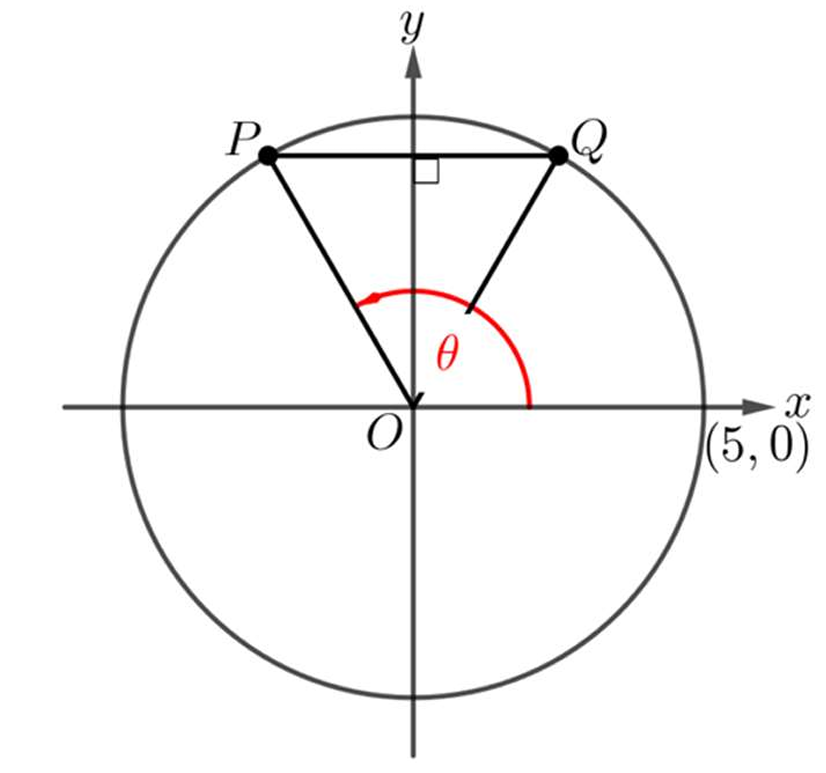
The coordinates of any point on a circle of radius $r$ are given by $(r \cos \theta, r \sin \theta)$, where $\theta$ is the angle from the positive x-axis. Here, $r=5$.
Since triangle $PQO$ is equilateral, the central angle $\angle POQ = \frac{\pi}{3}$ (which is $60^\circ$).
The triangle is symmetric about the y-axis, meaning the y-axis bisects $\angle POQ$. Thus, the angle between the positive y-axis and $OP$ is $\frac{1}{2} \cdot \frac{\pi}{3} = \frac{\pi}{6}$.
The positive y-axis itself is at an angle of $\frac{\pi}{2}$ relative to the positive x-axis.
Therefore, the total angle $\theta$ for point $P$ is the sum: $\theta = \frac{\pi}{2} + \frac{\pi}{6}$.
Calculating the sum: $\theta = \frac{3\pi}{6} + \frac{\pi}{6} = \frac{4\pi}{6} = \frac{2\pi}{3}$.
Hence, the coordinates of point $P$ are $\left( 5 \cos \frac{2\pi}{3}, 5 \sin \frac{2\pi}{3} \right)$.

Question

The figure above shows a circle of radius 10 along with the right triangle $PQO$. Which of the following gives the coordinates of point $P$?

(A) $\left( 10\cos\frac{\pi}{4}, 10\sin\frac{\pi}{4} \right)$

(B) $\left( -10\cos\frac{3\pi}{4}, 10\sin\frac{3\pi}{4} \right)$

(D) $\left( 10\cos\frac{5\pi}{4}, 10\sin\frac{5\pi}{4} \right)$

▶️ Answer/Explanation

Detailed solution

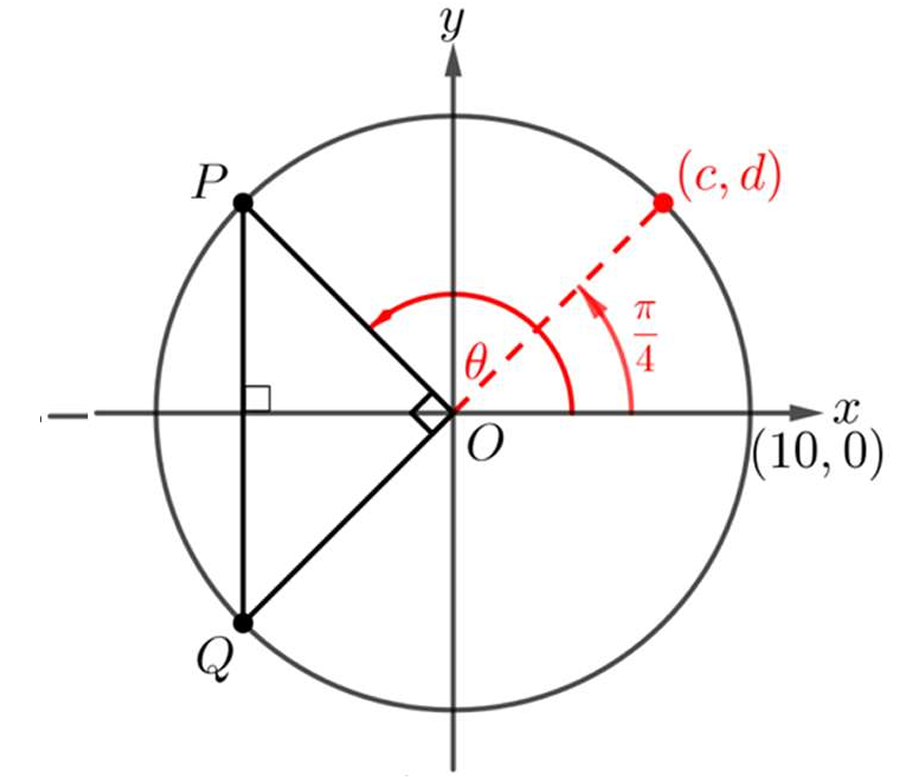
The point $P$ lies in the second quadrant where the x-coordinate is negative and the y-coordinate is positive.
Based on the symmetry shown in the diagram, point $P$ makes an angle of $\frac{3\pi}{4}$ with the positive x-axis, or has a reference angle of $\frac{\pi}{4}$ with the negative x-axis.
Using the reference angle $\frac{\pi}{4}$, the magnitude of the x-coordinate is $10\cos\frac{\pi}{4}$ and the y-coordinate is $10\sin\frac{\pi}{4}$.
Applying the signs for the second quadrant, the coordinates become $(-10\cos\frac{\pi}{4}, 10\sin\frac{\pi}{4})$.
Alternatively, checking the options: Option (C) is the only choice with a negative x-value and positive y-value, consistent with the second quadrant.
Therefore, the correct coordinates are given by choice (C).

Question

The function $ f $ is given by $ f(\theta) = 6 \cos \theta $. What are all values of $ \theta $, for $ 0 \le \theta < 2\pi $, where $ f(\theta) = -3 $?

(A) $ \theta = \frac{\pi}{6} $ and $ \theta = \frac{11\pi}{6} $

(B) $ \theta = \frac{5\pi}{6} $ and $ \theta = \frac{7\pi}{6} $

(D) $ \theta = \frac{2\pi}{3} $ and $ \theta = \frac{4\pi}{3} $

▶️ Answer/Explanation

Detailed solution

We are given the equation $ 6 \cos \theta = -3 $.
Isolate $ \cos \theta $ by dividing both sides by $ 6 $:
$ \cos \theta = -\frac{3}{6} = -\frac{1}{2} $
Since $ \cos \theta $ is negative, $ \theta $ must lie in Quadrant II or Quadrant III.
The reference angle for $ \cos \alpha = \frac{1}{2} $ is $ \frac{\pi}{3} $.
In Quadrant II: $ \theta = \pi – \frac{\pi}{3} = \frac{2\pi}{3} $.
In Quadrant III: $ \theta = \pi + \frac{\pi}{3} = \frac{4\pi}{3} $.
Therefore, the correct choice is (D).

Question

The function $g$ is given by $g(\theta) = 2 \sin \theta$. What are all values of $\theta$, for $0 \le \theta < 2\pi$, where $g(\theta) = \sqrt{2}$?

(A) $\theta = \frac{\pi}{4}$ and $\theta = \frac{3\pi}{4}$

(B) $\theta = \frac{\pi}{4}$ and $\theta = \frac{7\pi}{4}$

(D) $\theta = \frac{5\pi}{4}$ and $\theta = \frac{7\pi}{4}$

▶️ Answer/Explanation

Detailed solution

We start with the given equation: $2 \sin \theta = \sqrt{2}$.
Divide both sides by 2 to isolate the sine term: $\sin \theta = \frac{\sqrt{2}}{2}$.
Since $\sin \theta$ is positive, the angle $\theta$ must lie in Quadrant I or Quadrant II.
The reference angle for which $\sin \theta = \frac{\sqrt{2}}{2}$ is $\frac{\pi}{4}$.
In Quadrant I, the solution is $\theta = \frac{\pi}{4}$.
In Quadrant II, the solution is $\theta = \pi – \frac{\pi}{4} = \frac{3\pi}{4}$.
Therefore, the values are $\theta = \frac{\pi}{4}$ and $\theta = \frac{3\pi}{4}$.
Correct Option: (A)

Question

The function $ h $ is given by $ h(\theta) = 2 – \sin \theta $. What are all values of $ \theta $, for $ 0 \le \theta < 2\pi $, where $ h(\theta) = 2 $?

(A) $ \theta = \frac{\pi}{2} $ only

(B) $ \theta = \frac{3\pi}{2} $ only

(D) $ \theta = \frac{\pi}{2} $ and $ \theta = \frac{3\pi}{2} $

▶️ Answer/Explanation

Detailed solution

We are given the function $ h(\theta) = 2 – \sin \theta $ and set $ h(\theta) = 2 $.
Substituting the value, we get the equation: $ 2 – \sin \theta = 2 $.
Subtracting $ 2 $ from both sides simplifies to: $ -\sin \theta = 0 $, or $ \sin \theta = 0 $.
We look for solutions in the given interval $ 0 \le \theta < 2\pi $.
The sine function equals zero at integer multiples of $ \pi $, so $ \theta = 0 $ and $ \theta = \pi $.
Therefore, the correct values are $ \theta = 0 $ and $ \theta = \pi $, which matches option (C).

Question

The function $k$ is given by $k(\theta) = 1 – \cos \theta$. What are all values of $\theta$, for $0 \le \theta < 2\pi$, where $k(\theta) = 2$?

(A) $\theta = \frac{\pi}{2}$ only

(B) $\theta = \frac{3\pi}{2}$ only

(D) $\theta = \frac{\pi}{2}$ and $\theta = \frac{3\pi}{2}$

▶️ Answer/Explanation

Detailed solution

To find the value of $\theta$, we set the given function equal to 2:

\[1 – \cos \theta = 2\]

Subtract 1 from both sides to isolate the cosine term:

\[-\cos \theta = 1\]

Multiply both sides by -1:

\[\cos \theta = -1\]

We need to find $\theta$ in the interval $0 \le \theta < 2\pi$ where cosine is $-1$.

On the unit circle, $\cos \theta = -1$ only at $\theta = \pi$.

Thus, the correct option is (C).

Question

The figure shows the terminal ray of angle $\theta$, in standard position, intersecting the unit circle at position $P$ in the $xy$-plane. The function $f$ is given by $f(k) = \cos k$. For the angle $\alpha$ (not shown), $\theta < \alpha < \pi$. Which of the following is true?

(A) $f(\theta) = f(\alpha)$

(B) $f(\theta) < f(\alpha)$

(D) $f(\theta) < f(\alpha)$ and $f(\theta) > f(\alpha)$ are both true, depending on the angle of $\alpha$

▶️ Answer/Explanation

Detailed solution

The correct answer is (C).
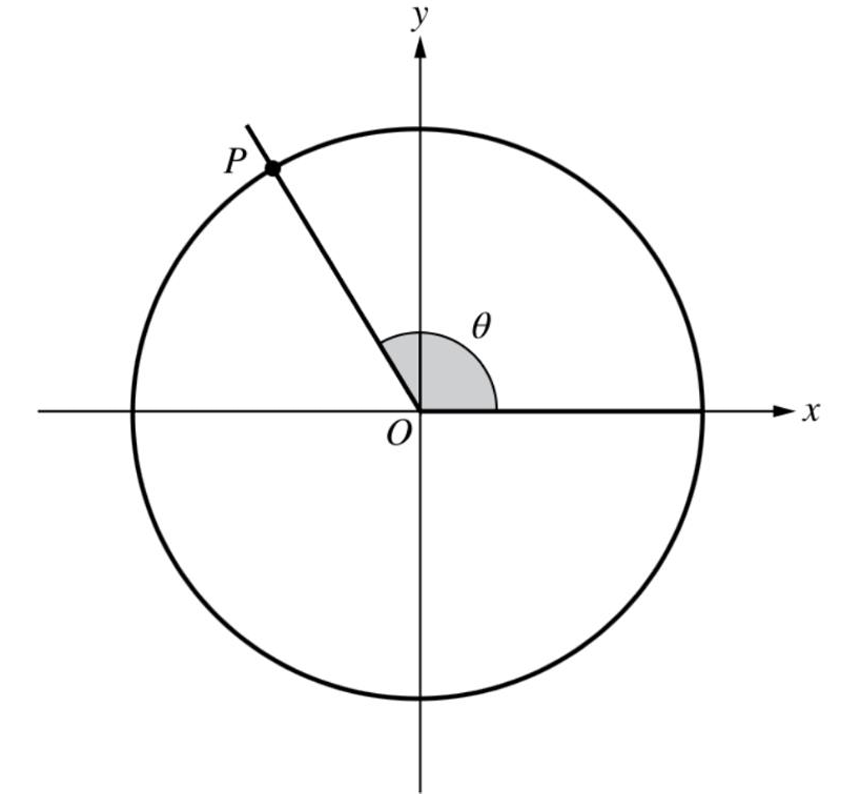
1. From the figure, the terminal ray of $\theta$ lies in the second quadrant. Thus, $\frac{\pi}{2} < \theta < \pi$.
2. The problem states that $\theta < \alpha < \pi$. This implies that $\alpha$ is also in the second quadrant but represents a larger rotation than $\theta$.
3. The function is defined as $f(k) = \cos k$. In the unit circle, the cosine of an angle corresponds to the $x$-coordinate of the point on the circle.
4. In the interval $(0, \pi)$, the cosine function is strictly decreasing. This means as the angle increases, the $x$-coordinate moves to the left (becomes more negative).
5. Since $\theta < \alpha$, the $x$-coordinate for angle $\alpha$ will be less than the $x$-coordinate for angle $\theta$.
6. Therefore, $\cos \theta > \cos \alpha$, which means $f(\theta) > f(\alpha)$.

Question

In the $xy$-plane, two different angles $\alpha$ and $\beta$ are in standard position and share a terminal ray. Based on this information, which of the following gives possible values for $\alpha$ and $\beta$?

(A) $\alpha = -\frac{\pi}{4}$ and $\beta = -\frac{7\pi}{4}$

(B) $\alpha = \frac{3\pi}{5}$ and $\beta = -\frac{3\pi}{5}$

(D) $\alpha = \frac{5\pi}{6}$ and $\beta = -\frac{\pi}{6}$

▶️ Answer/Explanation

Detailed solution

Angles in standard position that share a terminal ray are called coterminal angles.
For two angles to be coterminal, their difference must be an integer multiple of a full rotation, $2\pi$.
Let’s check the difference for option (C): $\beta – \alpha = \frac{8\pi}{3} – \frac{2\pi}{3}$.
Subtracting the numerators gives $\frac{6\pi}{3}$.
Simplifying the fraction results in $2\pi$.
Since the difference is exactly $2\pi$, the angles end at the same position.
Therefore, $\alpha$ and $\beta$ share a terminal ray.

Question

The figure shows a circle of radius $2$ along with four labeled points in the $xy$-plane. The measure of angle $COB$ is equal to the measure of angle $AOB$. What are the coordinates of point $B$?

(A) $\left( \cos\left( \frac{7\pi}{4} \right), \sin\left( \frac{7\pi}{4} \right) \right)$
(B) $\left( \sin\left( \frac{7\pi}{4} \right), \cos\left( \frac{7\pi}{4} \right) \right)$
(C) $\left( 2\cos\left( \frac{7\pi}{4} \right), 2\sin\left( \frac{7\pi}{4} \right) \right)$
(D) $\left( 2\sin\left( \frac{7\pi}{4} \right), 2\cos\left( \frac{7\pi}{4} \right) \right)$

▶️ Answer/Explanation

Detailed solution

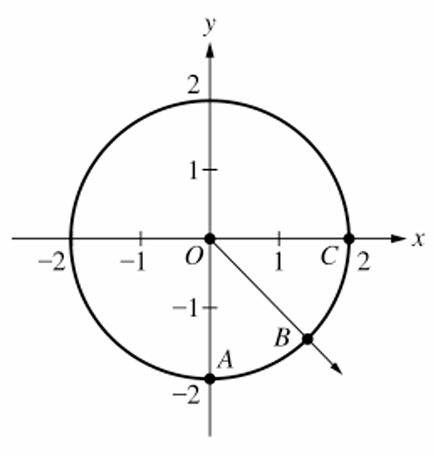
The circle has a radius $r = 2$.
Point $C$ is at $0$ radians and point $A$ is at $\frac{3\pi}{2}$ radians (or $-\frac{\pi}{2}$).
Since angle $COB$ equals angle $AOB$, $B$ is the midpoint of the arc between $0$ and $\frac{3\pi}{2}$ in the clockwise direction.
The angle $\theta$ for point $B$ in standard position is $2\pi – \frac{\pi}{4} = \frac{7\pi}{4}$ radians.
The coordinates of any point on a circle are given by $(r\cos\theta, r\sin\theta)$.
Substituting the values, the coordinates of $B$ are $\left( 2\cos\left( \frac{7\pi}{4} \right), 2\sin\left( \frac{7\pi}{4} \right) \right)$.
Therefore, the correct option is (C).

Question

In the $xy$-plane, an angle in standard position measures $\frac{5\pi}{6}$ radians. A circle centered at the origin has radius $4$. What are the coordinates of the point of intersection of the terminal ray of the angle and the circle?

(A) $(-2\sqrt{3}, 2)$
(B) $(-\frac{\sqrt{3}}{2}, \frac{1}{2})$
(C) $(\frac{\sqrt{3}}{2}, \frac{1}{2})$
(D) $(2\sqrt{3}, 2)$

▶️ Answer/Explanation

Detailed solution

The coordinates of a point on a circle are defined as $(x, y) = (r \cos \theta, r \sin \theta)$.
Given radius $r = 4$ and angle $\theta = \frac{5\pi}{6}$ radians.
The angle $\frac{5\pi}{6}$ is in the second quadrant, where cosine is negative and sine is positive.
Calculate $x = 4 \cos(\frac{5\pi}{6}) = 4 (-\frac{\sqrt{3}}{2}) = -2\sqrt{3}$.
Calculate $y = 4 \sin(\frac{5\pi}{6}) = 4 (\frac{1}{2}) = 2$.
The coordinates of the intersection point are $(-2\sqrt{3}, 2)$.
Therefore, the correct option is (A).

Question

Angles $A$ and $B$ are in standard position in the $xy$-plane. The measure of angle $A$ is $\frac{2\pi}{3}$ radians, and the measure of angle $B$ is $\frac{4\pi}{3}$ radians. The terminal rays of both angles intersect a circle centered at the origin with radius $20$. What is the distance between these two points of intersection: the circle and terminal ray of angle $A$, and the circle and terminal ray of angle $B$?

(A) $\cos\left(\frac{2\pi}{3}\right) – \cos\left(\frac{4\pi}{3}\right)$

(B) $20 \cos\left(\frac{2\pi}{3}\right) – 20 \cos\left(\frac{4\pi}{3}\right)$

(D) $20 \sin\left(\frac{2\pi}{3}\right) – 20 \sin\left(\frac{4\pi}{3}\right)$

▶️ Answer/Explanation

Detailed solution

The coordinates of a point on a circle of radius $r$ at angle $\theta$ are $(r \cos \theta, r \sin \theta)$.
Point $A$ is at $\left(20 \cos\left(\frac{2\pi}{3}\right), 20 \sin\left(\frac{2\pi}{3}\right)\right)$ and Point $B$ is at $\left(20 \cos\left(\frac{4\pi}{3}\right), 20 \sin\left(\frac{4\pi}{3}\right)\right)$.
Both angles have the same reference angle $\frac{\pi}{3}$, so their $x$-coordinates are both $20 \cos\left(\frac{2\pi}{3}\right) = 20 \cos\left(\frac{4\pi}{3}\right) = -10$.
Since the $x$-coordinates are identical, the points lie on a vertical line.
The distance is the difference between the $y$-coordinates: $y_A – y_B$.
This results in $20 \sin\left(\frac{2\pi}{3}\right) – 20 \sin\left(\frac{4\pi}{3}\right)$.
Thus, the correct option is (D).

Question

In the $xy$-plane, the terminal ray of angle $\theta$ in standard position intersects a circle of radius $r$ at the point $(10, -10\sqrt{3})$. What are the values of $\theta$ and $r$?

(A) $\theta = \frac{5\pi}{3}$ and $r = 10$
(B) $\theta = \frac{5\pi}{3}$ and $r = 20$
(C) $\theta = \frac{11\pi}{6}$ and $r = 10$
(D) $\theta = \frac{11\pi}{6}$ and $r = 20$

▶️ Answer/Explanation

Detailed solution

The radius is calculated using $r = \sqrt{x^2 + y^2} = \sqrt{10^2 + (-10\sqrt{3})^2}$.
This simplifies to $r = \sqrt{100 + 300} = \sqrt{400} = 20$.
The point $(10, -10\sqrt{3})$ lies in the fourth quadrant since $x > 0$ and $y < 0$.
The reference angle $\alpha$ is found by $\tan \alpha = \left| \frac{y}{x} \right| = \left| \frac{-10\sqrt{3}}{10} \right| = \sqrt{3}$.
Thus, $\alpha = \frac{\pi}{3}$, making the standard position angle $\theta = 2\pi – \frac{\pi}{3} = \frac{5\pi}{3}$.
Therefore, the correct values are $r = 20$ and $\theta = \frac{5\pi}{3}$.
The correct option is (B).

Question

The figure shows equilateral triangle $ABO$ with sides of length $10$ in the $xy$-plane. Segment $AB$ is perpendicular to the $x$-axis. The terminal ray of an angle $\theta$ (not shown) in standard position passes through the point $B$. What is the value of $10 \sin \theta$?

(A) $-5\sqrt{3}$
(B) $-\frac{\sqrt{3}}{2}$
(C) $\frac{1}{2}$
(D) $5$

▶️ Answer/Explanation

Detailed solution

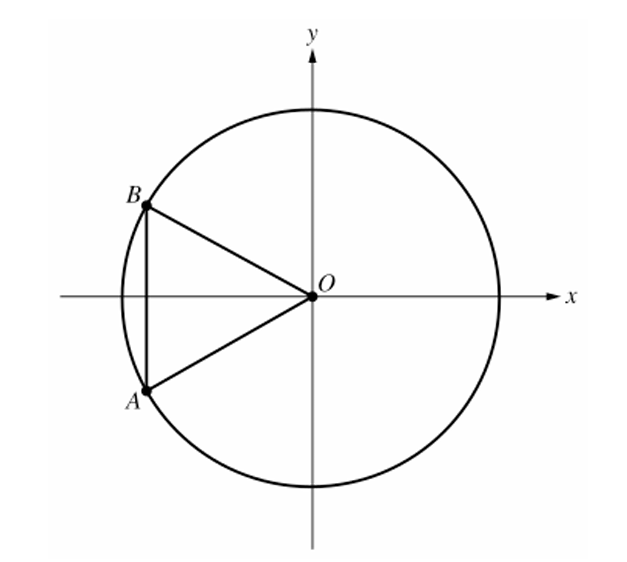
Since $\triangle ABO$ is equilateral with side length $10$, we have $OA = OB = AB = 10$.
Segment $AB$ is vertical and bisected by the $x$-axis due to the symmetry of the equilateral triangle centered at the origin horizontally.
The $y$-coordinate of point $B$ is half the length of side $AB$, which is $\frac{10}{2} = 5$.
Point $B$ lies on a circle centered at the origin with radius $r = OB = 10$.
In trigonometry, for any point $(x, y)$ on the terminal side of an angle $\theta$, $\sin \theta = \frac{y}{r}$.
Substituting the known values, we get $\sin \theta = \frac{5}{10} = \frac{1}{2}$.
The value of $10 \sin \theta$ is $10 \left( \frac{1}{2} \right) = 5$.
Therefore, the correct option is (D).

Question

The figure shows a spinner with eight congruent sectors in the $xy$-plane. The origin and three points are labeled. If the coordinates of $X$ are $\left( -\frac{5}{2}, \frac{-5\sqrt{3}}{2} \right)$, what is the measure of angle $XOB$?

(A) $\frac{\pi}{6}$
(B) $\frac{\pi}{3}$
(C) $\frac{7\pi}{6}$
(D) $\frac{4\pi}{3}$

▶️ Answer/Explanation

Detailed solution

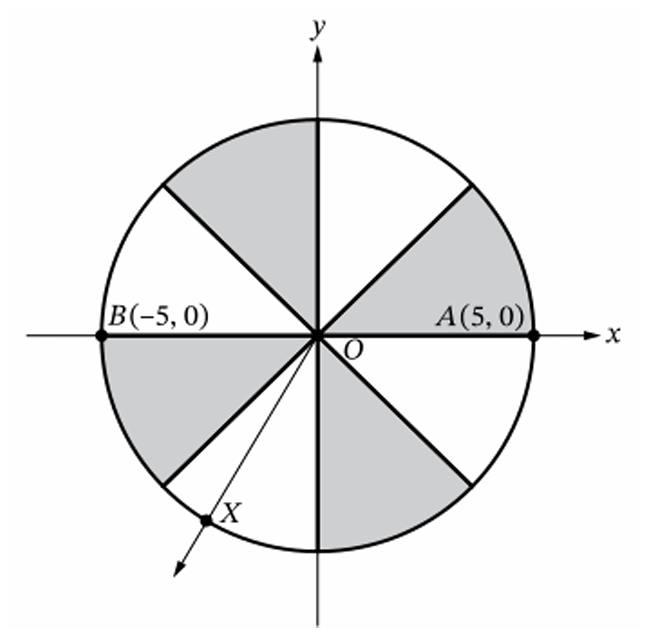
Point $B$ is on the negative $x$-axis, so its position corresponds to an angle of $\pi$ radians.
Point $X$ has coordinates $x = -\frac{5}{2}$ and $y = -\frac{5\sqrt{3}}{2}$ in Quadrant III.
The reference angle $\theta$ for $X$ is found using $\tan(\theta) = \left| \frac{y}{x} \right| = \left| \frac{-5\sqrt{3}/2}{-5/2} \right| = \sqrt{3}$.
This gives a reference angle of $\frac{\pi}{3}$ measured from the negative $x$-axis.
Since angle $XOB$ is the angle between the ray $OX$ and the ray $OB$ (the negative $x$-axis), the measure is simply the reference angle.
Therefore, the measure of angle $XOB$ is $\frac{\pi}{3}$.
The correct option is (B).

Question

The figure shows a circle centered at the origin with an angle of measure $\theta$ in standard position. The terminal ray of the angle intersects the circle at point $Q$. The coordinates of $P$ are $(4, 3)$ and the radius of the circle is $5$. What is the value of $\cos \theta$?

(A) $\cos \theta = -\frac{4}{5}$
(B) $\cos \theta = -\frac{3}{4}$
(C) $\cos \theta = \frac{3}{5}$
(D) $\cos \theta = \frac{4}{5}$

▶️ Answer/Explanation

Detailed solution

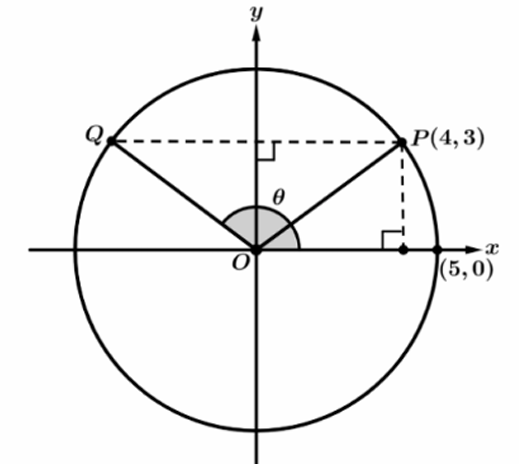
Point $P$ has coordinates $(4, 3)$, representing a horizontal distance of $4$ and a vertical distance of $3$.
Point $Q$ is the reflection of point $P$ across the $y$-axis, as shown by the dashed horizontal line.
The $x$-coordinate of $Q$ is the negative of the $x$-coordinate of $P$, so $Q = (-4, 3)$.
For any point $(x, y)$ on a circle of radius $r$, the cosine of the angle is defined as $\cos \theta = \frac{x}{r}$.
Given the radius $r = 5$ and the $x$-coordinate of $Q$ is $-4$.
Substituting these values gives $\cos \theta = \frac{-4}{5}$.
Therefore, the correct option is (A).

AP Precalculus -3.3 Sine and Cosine Values- MCQ Exam Style Questions - Effective Fall 2023