AP Precalculus -3.4 Sine and Cosine Graphs- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.4 Sine and Cosine Graphs- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.4 Sine and Cosine Graphs- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The figure gives the graphs of four functions labeled $ A $, $ B $, $ C $, and $ D $ in the $ xy $-plane. Which is the graph of $ f(x) = 2 \cos^{-1} x $?

(A) $ A $
(B) $ B $
(C) $ C $
(D) $ D $

▶️ Answer/Explanation

Detailed solution

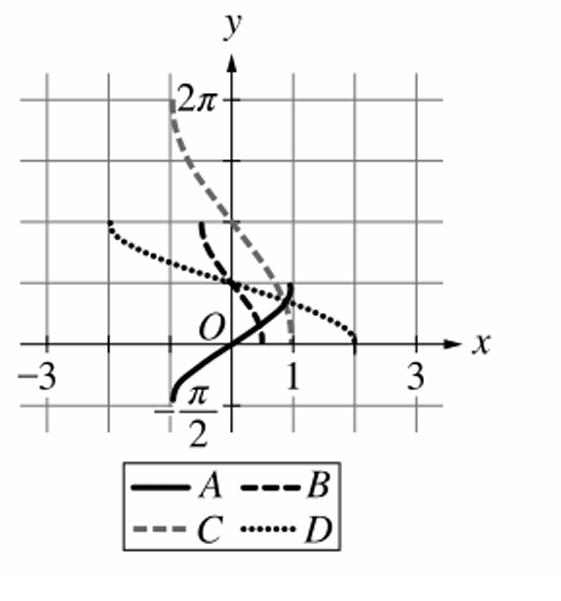
The function $ f(x) = 2\cos^{-1}x $ is a vertical stretch of $ y = \cos^{-1}x $ by factor 2.
– Domain: $ [-1, 1] $
– Range: $ [0, 2\pi] $ after stretch (since $ \cos^{-1}x $ ranges from $ 0 $ to $ \pi $, multiplying by 2 gives $ 0 $ to $ 2\pi $)
Graph $ C $ matches this vertical dilation.
✅ Answer: (C)

Question

Which of the following is the graph of $ f(x) = 2 \csc\left(\frac{2\pi}{3}x\right) $ in the $ xy $-plane?

▶️ Answer/Explanation

Detailed solution

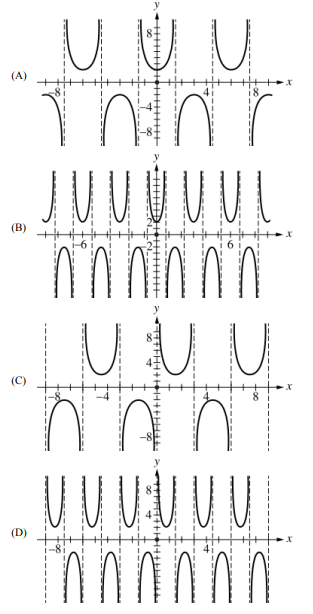
$ f(x) = 2\csc\left(\frac{2\pi}{3}x\right) $
– Cosecant is reciprocal of sine: $ \csc u = \frac{1}{\sin u} $
– Vertical asymptotes where $ \sin\left(\frac{2\pi}{3}x\right) = 0 $ → $ \frac{2\pi}{3}x = k\pi $ → $ x = \frac{3k}{2} = 1.5k $
– Period: $ \frac{2\pi}{2\pi/3} = 3 $
– Amplitude factor 2 outside → range: $ (-\infty, -2] \cup [2, \infty) $
Graph (D) matches these features: asymptotes every 1.5 units, period 3, branches outside $ [-2, 2] $.
✅ Answer: (D)

Question

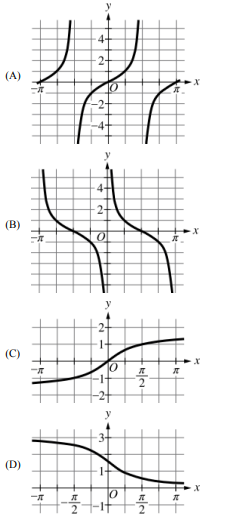
Which of the following is the graph of $ f(x) = \cot x $ in the $ xy $-plane?

▶️ Answer/Explanation

Detailed solution

$ f(x) = \cot x = \frac{\cos x}{\sin x} $
– Vertical asymptotes where $ \sin x = 0 $ → $ x = k\pi $
– Decreasing on each interval $ (k\pi, (k+1)\pi) $
– Passes through $ \left(\frac{\pi}{2} + k\pi, 0\right) $
Graph (B) matches this behavior.
✅ Answer: (B)

Question

The function $ g $ is given by $ g(\theta) = \cos \theta $. Which of the following describes $ g $ on the interval from $ \theta = \frac{3\pi}{2} $ to $ \theta = 2\pi $?

(A) $ g $ is decreasing, and the graph of $ g $ is concave down.
(B) $ g $ is decreasing, and the graph of $ g $ is concave up.
(C) $ g $ is increasing, and the graph of $ g $ is concave down.
(D) $ g $ is increasing, and the graph of $ g $ is concave up.

▶️ Answer/Explanation

Detailed solution

On $ \left( \frac{3\pi}{2}, 2\pi \right) $:
– Cosine increases from $ 0 $ to $ 1 $.
– The derivative $ g'(\theta) = -\sin\theta $ is positive (since sine is negative in Quadrant IV), so $ g $ is increasing.
– The second derivative $ g”(\theta) = -\cos\theta $ is negative (since cosine is positive in Quadrant IV), so concave down.
Thus: increasing and concave down.
✅ Answer: (C)

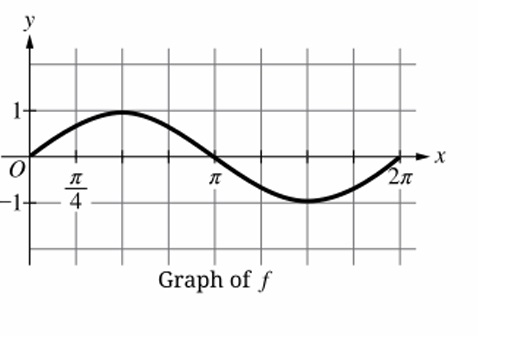
Question

The figure shows the graph of the function $ f $ in the $ xy $-plane. The function $ f $ is either a sine function or a cosine function. Consider an angle in standard position in another $ xy $-plane (not shown). The terminal ray of the angle intersects the unit circle at point $ P $. Which of the following is true about the relationship between $ f $ and $ P $?

(A) $ f $ gives the vertical distance of $ P $ from the $ x $-axis for angle measures from 0 to $ 2\pi $.
(B) $ f $ gives the horizontal distance of $ P $ from the $ y $-axis for angle measures from 0 to $ 2\pi $.
(C) $ f $ gives the vertical displacement of $ P $ from the $ x $-axis for angle measures from 0 to $ 2\pi $.
(D) $ f $ gives the horizontal displacement of $ P $ from the $ y $-axis for angle measures from 0 to $ 2\pi $.

▶️ Answer/Explanation

Detailed solution

The graph begins at the origin, increases to a maximum at $ \frac{\pi}{2} $, returns to zero at $ \pi $, goes to a minimum at $ \frac{3\pi}{2} $, and returns to zero at $ 2\pi $. This is the graph of $ f(x) = \sin x $.
On the unit circle, for an angle $ \theta $, the sine function gives the $ y $-coordinate of $ P $, which is the vertical displacement (signed distance) from the $ x $-axis.
Thus $ f(\theta) = \sin\theta $ gives the vertical displacement of $ P $ from the $ x $-axis.
✅ Answer: (C)

Question

The function $ f $ is given by $ f(\theta) = \cos \theta $, and the function $ g $ is given by $ g(\theta) = \sin \theta $. Which of the following describes $ f $ and $ g $ on the interval from $ \theta = \frac{\pi}{2} $ to $ \theta = \pi $?

(A) Both $ f $ and $ g $ are decreasing.
(B) Both $ f $ and $ g $ are increasing.
(C) $ f $ is decreasing, and $ g $ is increasing.
(D) $ f $ is increasing, and $ g $ is decreasing.

▶️ Answer/Explanation

Detailed solution

On $ \left( \frac{\pi}{2}, \pi \right) $:
– Cosine decreases from 0 to -1.
– Sine decreases from 1 to 0.
Thus both are decreasing.
✅ Answer: (A)

Question

The function $ f $ is given by $ f(\theta) = \sin \theta $. Which of the following describes $ f $ on the interval from $ \theta = \pi $ to $ \theta = \frac{3\pi}{2} $?

(A) $ f $ is decreasing, and the graph of $ f $ is concave down.
(B) $ f $ is decreasing, and the graph of $ f $ is concave up.
(C) $ f $ is increasing, and the graph of $ f $ is concave down.
(D) $ f $ is increasing, and the graph of $ f $ is concave up.

▶️ Answer/Explanation

Detailed solution

On $ \left( \pi, \frac{3\pi}{2} \right) $:
– Sine decreases from 0 to -1, so $ f $ is decreasing.
– Derivative $ f'(\theta) = \cos\theta $ is negative in Quadrant III, but becoming less negative (since cosine increases from -1 to 0), so slope is increasing → concave up.
– Second derivative $ f”(\theta) = -\sin\theta $: sine is negative in Quadrant III, so $ -\sin\theta > 0 $ → concave up.
Thus: decreasing and concave up.
✅ Answer: (B)

Question

The functions $ f $ and $ g $ are given by $ f(x) = \cos x $ and $ g(x) = \sin x $. In the $ xy $-plane, for how much of the interval $ 0 \leq x \leq 8\pi $ are the graphs of $ f $ and $ g $ both concave up?

(A) $ 0 $ units of $ x $
(B) $ \frac{\pi}{2} $ units of $ x $
(C) $ \pi $ units of $ x $
(D) $ 2\pi $ units of $ x $

▶️ Answer/Explanation

Detailed solution

Concavity:
– $ f(x)=\cos x $, $ f”(x)=-\cos x $ → concave up when $ -\cos x >0 $ → $ \cos x <0 $.
– $ g(x)=\sin x $, $ g”(x)=-\sin x $ → concave up when $ -\sin x >0 $ → $ \sin x <0 $.
Both concave up when $ \cos x <0 $ and $ \sin x <0 $ → Quadrant III: $ \pi < x < \frac{3\pi}{2} $ per period.
Length per period = $ \frac{\pi}{2} $.
Interval length $ 8\pi $ contains $ \frac{8\pi}{2\pi}=4 $ periods.
Total = $ 4 \times \frac{\pi}{2} = 2\pi $.
✅ Answer: (D)

Question

Which of the following best describes the behavior of $ g $ over the interval $ 0 < \theta < \frac{\pi}{2} $?

(A) $ g $ is increasing at an increasing rate.

(B) $ g $ is increasing at a decreasing rate.

(D) $ g $ is decreasing at a decreasing rate.

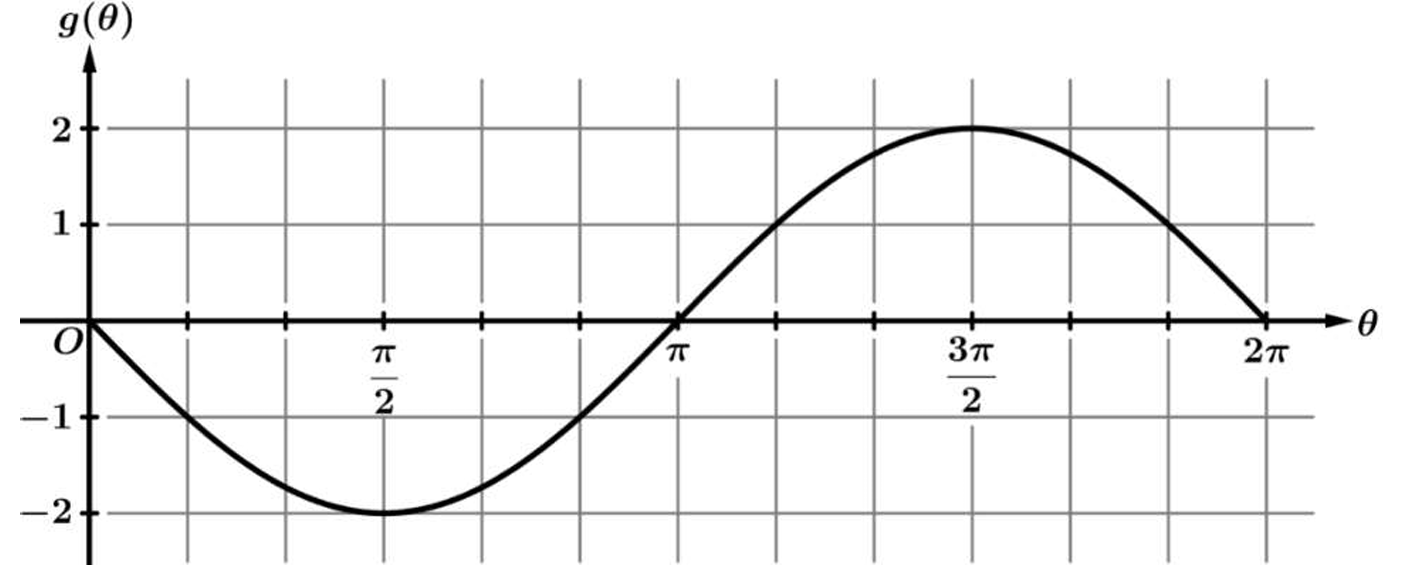
▶️ Answer/Explanation

Detailed solution

The correct answer is (C).

1. Analyze the function value: Looking at the graph in the interval $ 0 < \theta < \frac{\pi}{2} $, the curve goes downwards from the origin to a minimum. Since the values of $ g(\theta) $ are dropping, $ g $ is decreasing.

2. Analyze the rate of change (slope): The graph is concave up (curved like a cup) in this interval. Mathematically, the slope starts as a steep negative value and approaches zero (becomes less negative).

3. Interpret the rate: Since the slope is moving from a negative value towards zero (e.g., from -2 to -0.5), the numerical value of the rate is increasing.

Conclusion: Therefore, the function is decreasing (values going down) at an increasing rate (slope is increasing).

Question

Which of the following best describes the behavior of $ g $ over the interval $ \frac{\pi}{2} < \theta < \pi $?

(A) $ g $ is positive and increasing.

(B) $ g $ is positive and decreasing.

(D) $ g $ is negative and decreasing.

▶️ Answer/Explanation

Detailed solution

Step 1: Identify the interval on the horizontal axis from $ \theta = \frac{\pi}{2} $ to $ \theta = \pi $.
Step 2: Observe the position of the graph relative to the horizontal axis. In this region, the curve is strictly below the $ \theta $-axis, which means $ g(\theta) $ is negative.
Step 3: Analyze the slope of the curve. Starting from $ \theta = \frac{\pi}{2} $, the graph is at its minimum value of $ -2 $ and moves upwards to $ 0 $ at $ \theta = \pi $.
Step 4: Since the $ y $-values are getting larger (moving from negative towards zero), the function is increasing.
Step 5: Therefore, on the interval $ \frac{\pi}{2} < \theta < \pi $, $ g $ is negative and increasing.
Step 6: Comparing this with the given options, it corresponds to option (C).

Question

Which of the following best describes how the rate of change of $ g $ is changing over the interval $ \pi < \theta < \frac{3\pi}{2} $?

(A) The rate of change of $ g $ is increasing because the graph of $ g $ is concave up on the interval $ \pi < \theta < \frac{3\pi}{2} $.

(B) The rate of change of $ g $ is decreasing because the graph of $ g $ is concave up on the interval $ \pi < \theta < \frac{3\pi}{2} $.

(C) The rate of change of $ g $ is increasing because the graph of $ g $ is concave down on the interval $ \pi < \theta < \frac{3\pi}{2} $.

(D) The rate of change of $ g $ is decreasing because the graph of $ g $ is concave down on the interval $ \pi < \theta < \frac{3\pi}{2} $.

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

1. Analyze the Graph Shape: Observe the graph on the interval $ \pi < \theta < \frac{3\pi}{2} $. The curve is shaped like an inverted bowl, bending downwards.
2. Determine Concavity: This downward bending shape indicates that the graph is concave down on this interval.
3. Connect to Rate of Change: The “rate of change of $ g $” is the first derivative, $ g’ $. Concavity is determined by the second derivative, $ g” $.
4. Interpret Concavity: If a function is concave down, its derivative (slope) is decreasing.
5. Visual Verification: At $ \theta = \pi $, the slope is positive and steep. As $ \theta $ approaches $ \frac{3\pi}{2} $, the tangent line flattens out (slope approaches 0). Thus, the slope is decreasing.
6. Conclusion: The rate of change is decreasing because the graph is concave down.

Question

The graph of $g(\theta)$ is given. Which of the following best describes the rate of change of $g$ over the interval $\frac{3\pi}{2} < \theta < 2\pi$?

(A) The rate of change of $g$ is positive and increasing.

(B) The rate of change of $g$ is positive and decreasing.

(D) The rate of change of $g$ is negative and decreasing.

▶️ Answer/Explanation

Detailed solution

The correct option is (D).

1. Identify the relevant section of the graph: The interval $\frac{3\pi}{2} < \theta < 2\pi$ corresponds to the curve segment after the peak, descending towards the x-axis.
2. Determine the sign of the rate of change: In this interval, the function values $g(\theta)$ are dropping from the maximum (2) down to 0.
3. Since the function is strictly decreasing, the slope of the tangent (rate of change) is negative.
4. Analyze the behavior of the rate of change: At the peak $\theta = \frac{3\pi}{2}$, the slope is zero (horizontal tangent).
5. As $\theta$ increases towards $2\pi$, the graph becomes steeper in the downward direction.
6. This means the slope values are changing from 0 to negative numbers (e.g., -1, -2).
7. Since the value of the slope is going down (becoming more negative), the rate of change is decreasing.
8. Therefore, the rate of change of $g$ is negative and decreasing.

Question

On the interval $\left( 0, \frac{\pi}{2} \right)$, which of the following is true about $h$?

(A) $h$ is positive and increasing.

(B) $h$ is positive and decreasing.

(D) $h$ is negative and decreasing.

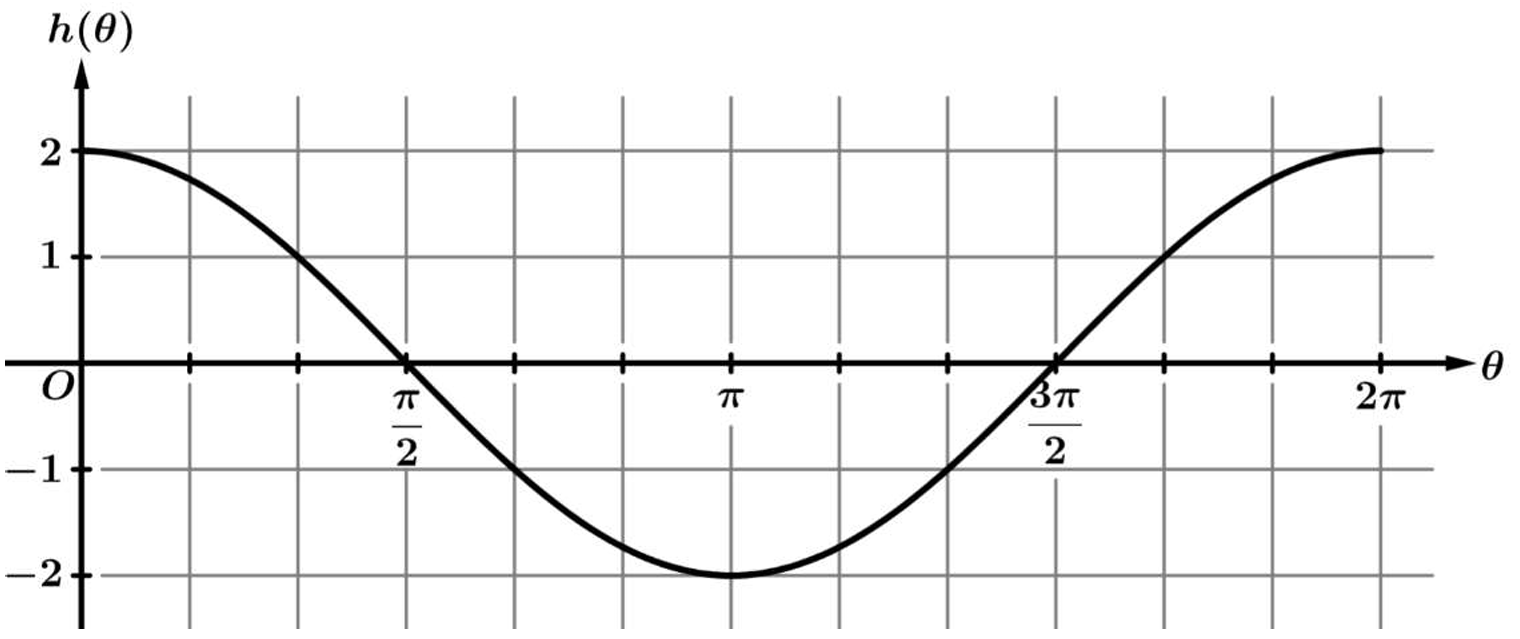
▶️ Answer/Explanation

Detailed solution

The correct answer is (B).

1. First, locate the interval $\left( 0, \frac{\pi}{2} \right)$ on the horizontal axis ($\theta$-axis) of the provided graph.

2. Observe the position of the function $h(\theta)$ relative to the x-axis. In this specific interval, the graph is entirely above the x-axis, which means $h$ is positive.

3. Next, observe the direction of the curve as you move from left to right (from $0$ to $\frac{\pi}{2}$).

4. The value of $h(\theta)$ starts at $2$ and goes down to $0$. A downward slope indicates that the function is decreasing.

5. Therefore, on the interval $\left( 0, \frac{\pi}{2} \right)$, $h$ is positive and decreasing.

Question

On the interval $\left(\frac{\pi}{2}, \pi\right)$, which of the following is true about $h$?

(A) $h$ is positive and increasing.

(B) $h$ is positive and decreasing.

(D) $h$ is negative and decreasing.

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

1. Identify the interval $\left(\frac{\pi}{2}, \pi\right)$ on the horizontal $\theta$-axis.
2. Observe the position of the curve relative to the horizontal axis. The graph lies below the x-axis in this interval, meaning the function values $h(\theta)$ are negative.
3. Analyze the slope of the curve as you move from left to right. The graph slopes downwards, going from a value of $0$ at $\frac{\pi}{2}$ to $-2$ at $\pi$.
4. Since the function values are falling, $h$ is decreasing.
5. Therefore, on this interval, $h$ is both negative and decreasing.

Question

On the interval $\left( \pi, \frac{3\pi}{2} \right)$, which of the following is true about $h$?

(A) $h$ is positive and increasing.

(B) $h$ is positive and decreasing.

(D) $h$ is negative and decreasing.

▶️ Answer/Explanation

Detailed solution

1. Identify the interval on the horizontal axis ($ \theta $-axis), which is from $ \pi $ to $ \frac{3\pi}{2} $.

2. Observe the position of the graph relative to the x-axis. In this interval, the curve lies entirely below the x-axis, meaning the value of $ h $ is negative.

3. Observe the direction of the curve. As we move from left to right (from $ \pi $ to $ \frac{3\pi}{2} $), the graph goes upwards from the minimum value of $-2$ towards $0$.

4. Since the graph is rising, the function is increasing.

5. Therefore, on the interval $\left( \pi, \frac{3\pi}{2} \right)$, $ h $ is both negative and increasing.

Correct Option: (C)

Question

On the interval $\left(\frac{3\pi}{2}, 2\pi\right)$, which of the following is true about $h$?

(A) $h$ is positive and increasing.

(B) $h$ is positive and decreasing.

(D) $h$ is negative and decreasing.

▶️ Answer/Explanation

Detailed solution

(A)
1. First, identify the relevant section of the graph on the horizontal axis between $\theta = \frac{3\pi}{2}$ and $\theta = 2\pi$.
2. Check the sign of the function: The curve lies entirely above the horizontal axis (the $\theta$-axis) in this interval, which means $h(\theta) > 0$ (it is positive).
3. Check the direction of the function: As you move from left to right along the interval, the curve goes upwards, rising from $0$ to $2$.
4. Since the curve is going up, the slope is positive, meaning the function is increasing.
5. Therefore, $h$ is positive and increasing.

Question

Which of the following correctly describes how the rate of change of $ h $ is changing on the interval $ \left(0, \frac{\pi}{2}\right) $?

(A) The rate of change of $ h $ is increasing because the graph of $ h $ is concave up.

(B) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave up.

(D) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave down.

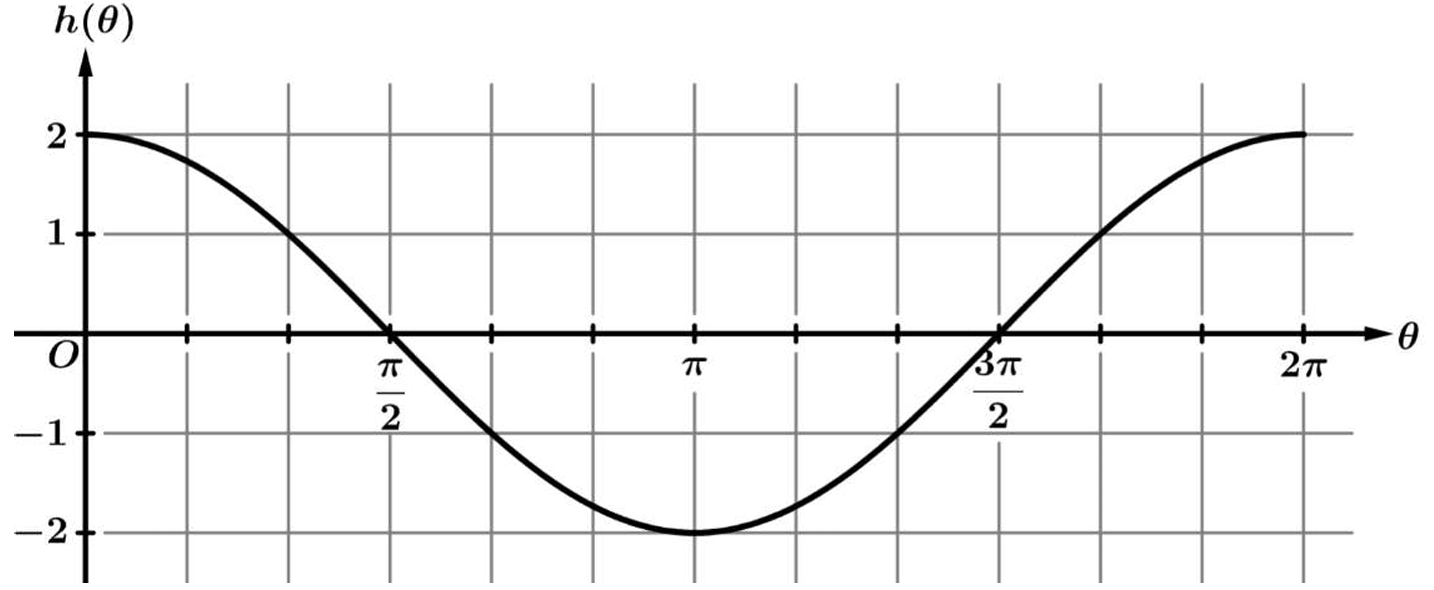
▶️ Answer/Explanation

Detailed solution

The “rate of change of $ h $” refers to the slope of the function (the first derivative, $ h’ $).

The change in this rate is determined by the concavity of the graph (the second derivative, $ h” $).

On the interval $ \left(0, \frac{\pi}{2}\right) $, the graph of $ h $ curves downwards, resembling an upside-down bowl.

This shape indicates that the graph is concave down in this region.

When a graph is concave down, the slope of the tangent lines decreases as $ \theta $ increases.

Therefore, the rate of change of $ h $ is decreasing because the graph of $ h $ is concave down.

Correct Option: (D)

Question

Which of the following correctly describes how the rate of change of $h$ is changing on the interval $\left(\frac{\pi}{2}, \pi\right)$?

(A) The rate of change of $h$ is increasing because the graph of $h$ is concave up.

(B) The rate of change of $h$ is decreasing because the graph of $h$ is concave up.

(D) The rate of change of $h$ is decreasing because the graph of $h$ is concave down.

▶️ Answer/Explanation

Detailed solution

The correct answer is (A).

1. Analyze the Graph Shape: Observe the curve of $h(\theta)$ on the interval $\left(\frac{\pi}{2}, \pi\right)$. The graph curves upwards, resembling the shape of a bowl “holding water.”
2. Determine Concavity: This upward curvature indicates that the function is concave up on this specific interval.
3. Relate Concavity to Rate of Change: By definition, if the graph of a function is concave up, its first derivative (which represents the rate of change) is increasing.
4. Verify with Slopes: At $\theta = \frac{\pi}{2}$, the slope is steep and negative. As $\theta$ approaches $\pi$, the slope becomes less negative and reaches zero. Since the slope values are rising from a negative number to zero, the rate of change is increasing.
5. Conclusion: Therefore, the rate of change of $h$ is increasing because the graph of $h$ is concave up.

Question

Which of the following correctly describes how the rate of change of $ h $ is changing on the interval $ \left( \pi, \frac{3\pi}{2} \right) $?

(A) The rate of change of $ h $ is increasing because the graph of $ h $ is concave up.

(B) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave up.

(D) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave down.

▶️ Answer/Explanation

Detailed solution

The correct answer is (A).

1. First, identify the section of the graph on the interval $ \left( \pi, \frac{3\pi}{2} \right) $. In this region, the curve is bending upwards (holding water), which means the graph is concave up.
2. The “rate of change of $ h $” refers to the first derivative, $ h'(\theta) $, or the slope of the tangent line.
3. “How the rate of change is changing” refers to the second derivative, $ h”(\theta) $.
4. When a graph is concave up, its second derivative is positive ($ h”(\theta) > 0 $).
5. A positive second derivative implies that the first derivative (the rate of change) is increasing.
6. Visually, the slope of the graph starts at $ 0 $ at $ \theta = \pi $ and becomes steeper in the positive direction as it approaches $ \frac{3\pi}{2} $.

Question

Which of the following correctly describes how the rate of change of $ h $ is changing on the interval $ \left( \frac{3\pi}{2}, 2\pi \right) $?

(A) The rate of change of $ h $ is increasing because the graph of $ h $ is concave up.

(B) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave up.

(D) The rate of change of $ h $ is decreasing because the graph of $ h $ is concave down.

▶️ Answer/Explanation

Detailed solution

The correct answer is (D).

The “rate of change of $ h $” represents the slope of the graph’s tangent line.

The phrase “how the rate of change is changing” refers to the concavity of the graph (the second derivative).

On the interval $ \left( \frac{3\pi}{2}, 2\pi \right) $, the graph curves downwards, resembling an inverted bowl.

This geometric shape indicates that the graph is concave down on this interval.

Mathematically, when a graph is concave down, its slope (rate of change) is strictly decreasing.

Therefore, the rate of change of $ h $ is decreasing because the graph of $ h $ is concave down.

Question

Let $ f $ be a sinusoidal function. The graph of $ y = f(x) $ is given in the $ xy $-plane. What is the period of $ f $?

(A) $ 2 $

(B) $ 3 $

(D) $ 6 $

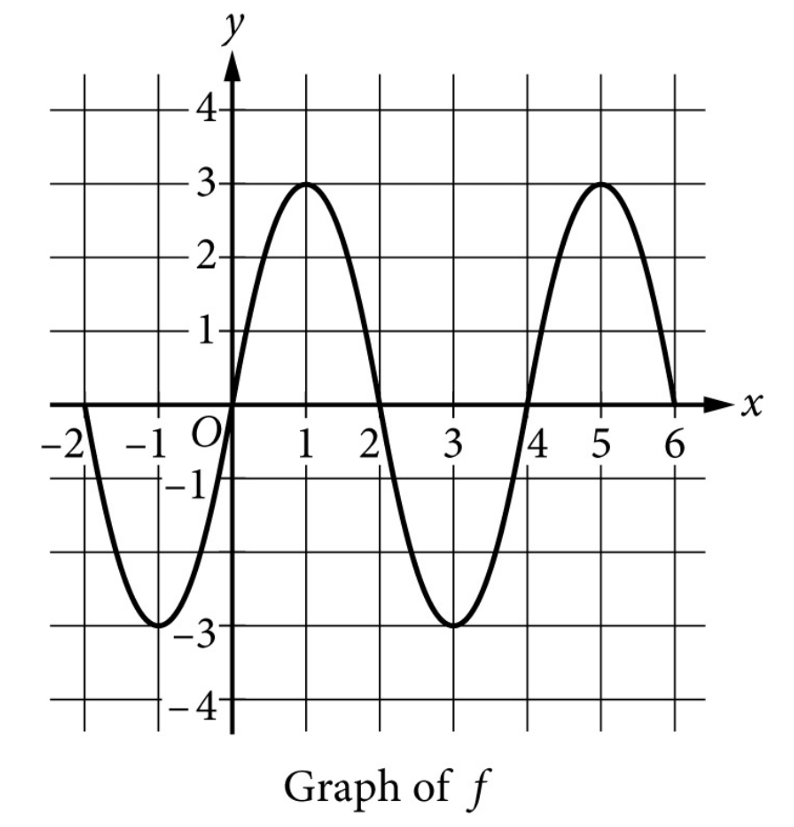
▶️ Answer/Explanation

Detailed solution

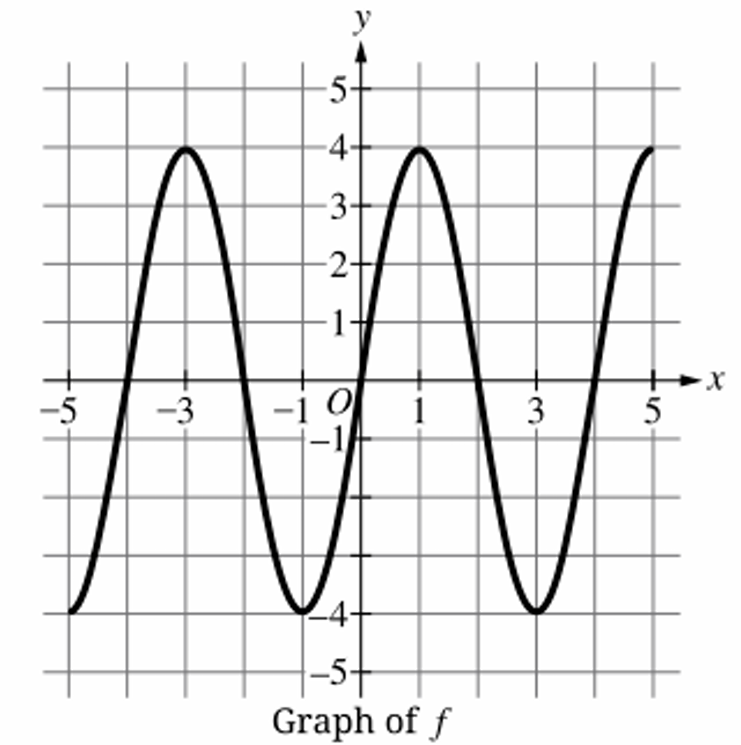
The period is the horizontal length of one complete cycle of the function’s graph.
We can find this by measuring the distance between two consecutive peaks (maximums).
Looking at the graph, the first peak is located at $ x = 1 $.
The next consecutive peak is located at $ x = 5 $.
The period is calculated as the difference between these x-values: $ 5 – 1 = 4 $.
Alternatively, a full cycle starting from the origin at $ x = 0 $ completes at $ x = 4 $.
Thus, the period of $ f $ is $ 4 $.

Correct Answer: (C)

Question

The function $f$ is given by $f(x) = 2 \sin(4x) + \cos(2x)$. Using the period of $f$, which of the following is the number of complete cycles of the graph of $f$ in the $xy$-plane on the interval $0 \le x \le 1000$?

(A) $159$

(B) $318$

(D) $636$

▶️ Answer/Explanation

Detailed solution

The period of the term $ \sin(4x) $ is $ \frac{2\pi}{4} = \frac{\pi}{2} $.
The period of the term $ \cos(2x) $ is $ \frac{2\pi}{2} = \pi $.
The fundamental period of $ f(x) $ is the least common multiple (LCM) of $ \frac{\pi}{2} $ and $ \pi $, which is $ \pi $.
The total length of the given interval is $ 1000 – 0 = 1000 $.
The number of cycles is found by dividing the interval length by the period: $ \frac{1000}{\pi} $.
Using the approximation $ \pi \approx 3.14159 $, we get $ \frac{1000}{3.14159} \approx 318.31 $.
Therefore, the number of complete cycles is the integer part, which is $ 318 $.
Correct Option: (B)

Question

The graph of the function $f$ is given in the $xy$-plane. Which of the following functions has the same period as $f$?

(A)

(B)

(C)

(D)

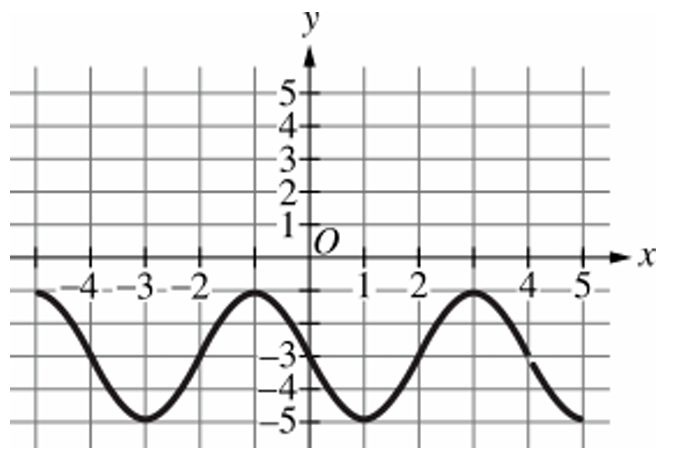
▶️ Answer/Explanation

Detailed solution

The period of a periodic function is the horizontal distance required for the graph to complete one full cycle.
By observing the graph of $f$, a peak occurs at $x = 1$ and the next peak occurs at $x = 5$.
Therefore, the period of $f$ is calculated as $5 – 1 = 4$ units.
Looking at Option (A), a peak occurs at $x = 0$ and the next peak occurs at $x = 4$.
The period for Option (A) is $4 – 0 = 4$ units, which matches function $f$.
Other options have different periods: (B) has a period of $2$, (C) has a period of $8$, and (D) has a period of $6$.
Thus, the function in Option (A) has the same period as $f$.

Question

The figure shows the terminal ray of angle $\theta$, in standard position, intersecting the unit circle at point $P$ in the $xy$-plane. The function $g$ is given by $g(z) = \cos z$. For the angle $\omega$ (not shown), $\theta < \omega < \pi$. Which of the following is true?

(A) $g(\omega) < g(\theta)$

(B) $g(\omega) > g(\theta)$

(D) Depending on the value of $\omega$, sometimes $g(\omega) < g(\theta)$ and sometimes $g(\omega) > g(\theta)$.

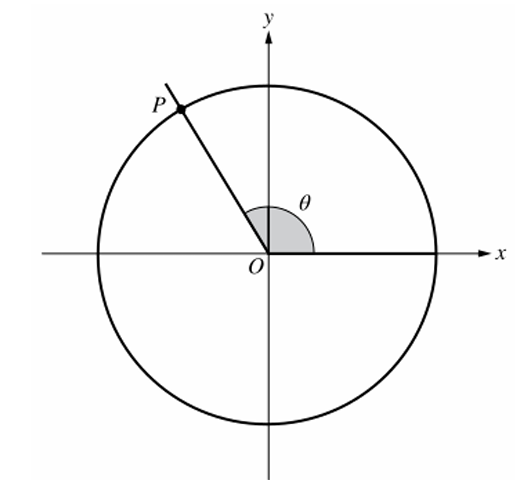
▶️ Answer/Explanation

Detailed solution

The function is defined as $g(z) = \cos z$.
The angle $\theta$ is in the second quadrant, where $\frac{\pi}{2} < \theta < \pi$.
We are given the interval $\theta < \omega < \pi$.
In the second quadrant, the cosine function is strictly decreasing.
As the angle $z$ increases from $\theta$ toward $\pi$, the $x$-coordinate on the unit circle moves left.
Therefore, if $\omega > \theta$, then $\cos \omega < \cos \theta$.
This means $g(\omega) < g(\theta)$, making (A) the correct choice.

Question

The figure shows the terminal ray of angle $\theta$, in standard position, intersecting the unit circle at point $P$ in the $xy$-plane. The function $f$ is given by $f(z) = \sin z$. For the angle $\beta$ (not shown), $\frac{\pi}{2} < \beta < \theta$. Which of the following is true?

(A) $f(\beta) < f(\theta)$

(B) $f(\beta) > f(\theta)$

(D) Depending on the value of $\beta$, sometimes $f(\beta) < f(\theta)$ and sometimes $f(\beta) > f(\theta)$.

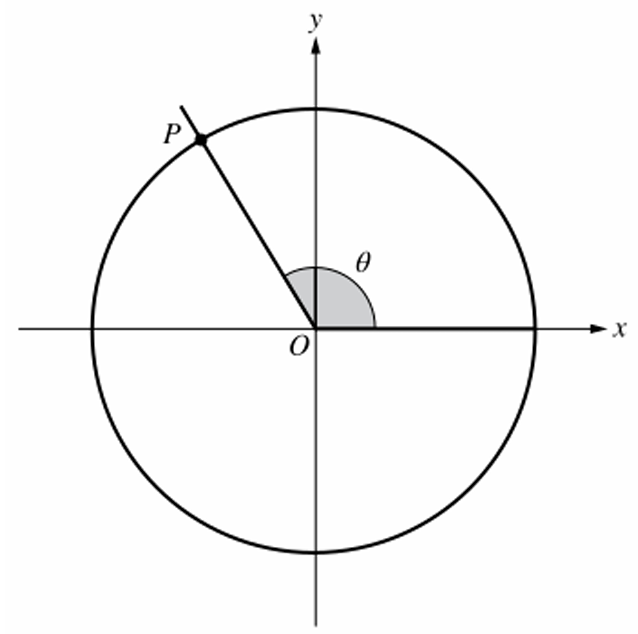
▶️ Answer/Explanation

Detailed solution

The point $P$ is in the second quadrant, meaning $\frac{\pi}{2} < \theta < \pi$.
The function is defined as $f(z) = \sin z$.
In the interval $(\frac{\pi}{2}, \pi)$, the sine function is strictly decreasing.
Given the inequality $\frac{\pi}{2} < \beta < \theta$, both angles are in the second quadrant.
Since $\beta < \theta$ and sine is decreasing here, it follows that $\sin \beta > \sin \theta$.
Therefore, $f(\beta) > f(\theta)$, which corresponds to option (B).

Question

The function $g$ is given by $g(\theta) = \cos \theta$. Which of the following describes $g$ on the interval from $\theta = \frac{3\pi}{2}$ to $\theta = 2\pi$ ?

(A) $g$ is decreasing, and the graph of $g$ is concave down.
(B) $g$ is decreasing, and the graph of $g$ is concave up.
(C) $g$ is increasing, and the graph of $g$ is concave down.
(D) $g$ is increasing, and the graph of $g$ is concave up.

▶️ Answer/Explanation

Detailed solution

The first derivative $g'(\theta) = -\sin \theta$ is positive on $(\frac{3\pi}{2}, 2\pi)$, so $g$ is increasing.
The second derivative $g”(\theta) = -\cos \theta$ is negative on $(\frac{3\pi}{2}, 2\pi)$ because $\cos \theta > 0$ in Quadrant IV.
Since $g”(\theta) < 0$, the graph of $g$ is concave down.
In the fourth quadrant, $\cos \theta$ increases from $0$ to $1$.
The curvature curves “downward” toward the horizontal axis as it approaches the maximum.
Therefore, the correct description is that $g$ is increasing and concave down.
Correct Option: (C)

Question

The function $f$ is given by $f(\theta) = \cos \theta$, and the function $g$ is given by $g(\theta) = \sin \theta$. Which of the following describes $f$ and $g$ on the interval from $\theta = \frac{\pi}{2}$ to $\theta = \pi$?

(A) Both $f$ and $g$ are decreasing.

(B) Both $f$ and $g$ are increasing.

(D) $f$ is increasing, and $g$ is decreasing.

▶️ Answer/Explanation

Detailed solution

The interval $[\frac{\pi}{2}, \pi]$ corresponds to the Second Quadrant of the unit circle.
For $f(\theta) = \cos \theta$, the value moves from $\cos(\frac{\pi}{2}) = 0$ down to $\cos(\pi) = -1$.
Since the values are getting smaller, $f$ is decreasing.
For $g(\theta) = \sin \theta$, the value moves from $\sin(\frac{\pi}{2}) = 1$ down to $\sin(\pi) = 0$.
Since the values are getting smaller, $g$ is decreasing.
Therefore, both $f$ and $g$ are decreasing on this interval.
The correct option is (A).

Question

The function $f$ is given by $f(\theta) = \sin \theta$. Which of the following describes $f$ on the interval from $\theta = \pi$ to $\theta = \frac{3\pi}{2}$?

(A) $f$ is decreasing, and the graph of $f$ is concave down.
(B) $f$ is decreasing, and the graph of $f$ is concave up.
(C) $f$ is increasing, and the graph of $f$ is concave down.
(D) $f$ is increasing, and the graph of $f$ is concave up.

▶️ Answer/Explanation

Detailed solution

The correct option is (B).
On the interval $[\pi, \frac{3\pi}{2}]$, the value of $\sin \theta$ goes from $0$ to $-1$, meaning $f$ is decreasing.
The first derivative $f'(\theta) = \cos \theta$ is negative in the third quadrant, confirming the function is decreasing.
The second derivative $f”(\theta) = -\sin \theta$ is positive on this interval because $\sin \theta$ is negative.
Since $f”(\theta) > 0$, the graph of $f$ is concave up.
Therefore, $f$ is decreasing and concave up on the given interval.

Question

The figure shows a robotic arm rotating in a circular counterclockwise direction that completes one rotation every $2$ seconds. Point $S$ is on the tip of the arm, and point $X$ does not move. As the arm rotates at a constant speed, the height of $S$ above $X$ periodically increases and decreases. At time $t = 0$ seconds, $S$ is at its lowest position, $6$ inches directly below $X$. At its highest position, $S$ is $20$ inches directly above $X$.

The sinusoidal function $h$ models the height of $S$ above $X$, in inches, as a function of time $t$, in seconds. A positive value of $h(t)$ indicates $S$ is above $X$; a negative value of $h(t)$ indicates $S$ is below $X$.

Part A
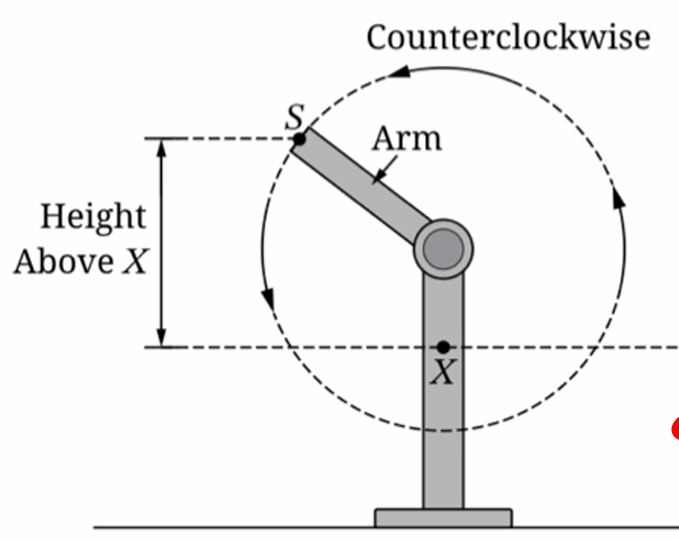
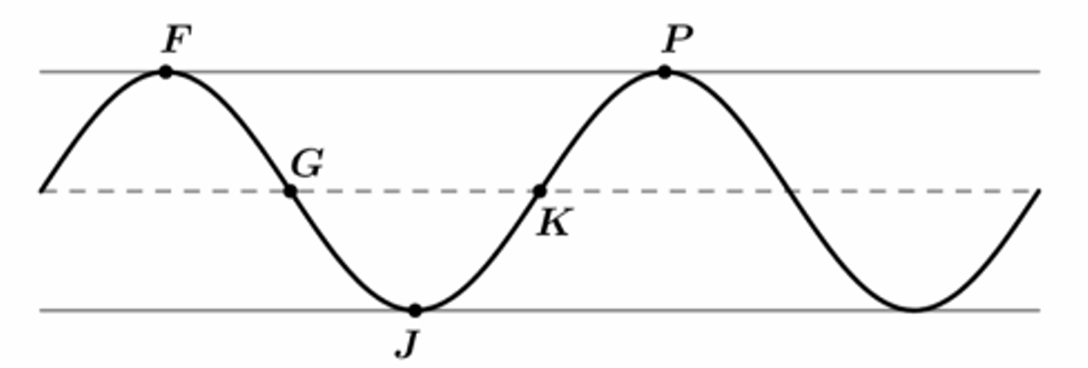
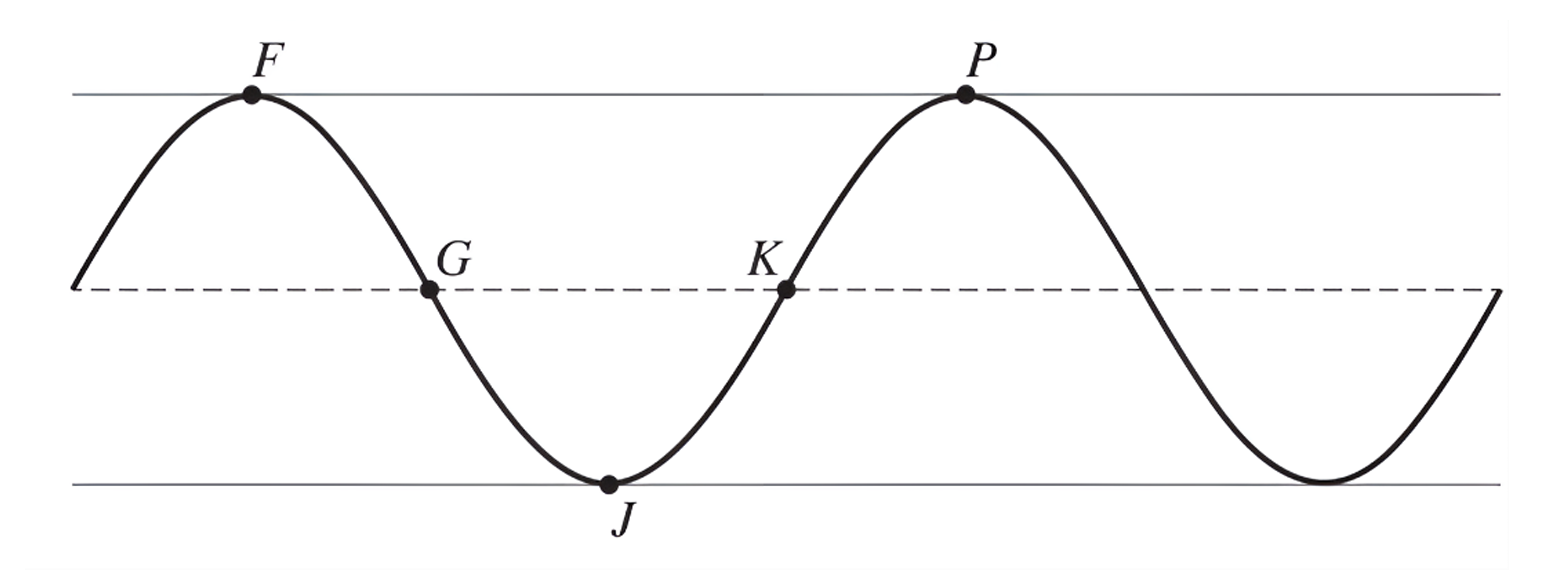
The graph of $h$ and its dashed midline for two full cycles is shown. Five points, $F, G, J, K,$ and $P$, are labeled on the graph. Determine possible coordinates $(t, h(t))$ for the five points.

Part B
The function $h$ can be written in the form $h(t) = a \cos(b(t + c)) + d$. Find values of constants $a, b, c,$ and $d$.

Part C
Refer to the graph of $h$ in part (A). The $t$-coordinate of $K$ is $t_1$, and the $t$-coordinate of $P$ is $t_2$.
(i) On the interval $(t_1, t_2)$, which of the following is true about $h$?
a. $h$ is positive and increasing.
b. $h$ is positive and decreasing.
c. $h$ is negative and increasing.
d. $h$ is negative and decreasing.
(ii) Describe how the rate of change of $h$ is changing on the interval $(t_1, t_2)$.

▶️ Answer/Explanation

Detailed solution

Part A: Coordinates of Points

At $t = 0$, $S$ is at its minimum height $-6$ (below $X$).
The maximum height is $20$.
The midline $d = \frac{20 + (-6)}{2} = 7$.
The period is $2$ seconds.
The graph starts at a minimum at $t = 0$, reaches midline at $t = 0.5$, maximum at $t = 1$, midline at $t = 1.5$, and minimum at $t = 2$.
Based on the visual positions in the provided graph:
$F$ (first maximum): $(1, 20)$
$G$ (midline, decreasing): $(1.5, 7)$
$J$ (minimum): $(2, -6)$
$K$ (midline, increasing): $(2.5, 7)$
$P$ (second maximum): $(3, 20)$

Part B: Finding Constants

$a$ (Amplitude) $= \frac{20 – (-6)}{2} = 13$. Since we use $\cos$ and start at a minimum, $a = -13$ (or use a phase shift).
$d$ (Vertical shift/Midline) $= 7$.
$b$ (Frequency factor) $= \frac{2\pi}{\text{period}} = \frac{2\pi}{2} = \pi$.
$c$ (Phase shift): For $h(t) = a \cos(b(t+c)) + d$, if $a = -13$, then at $t=0$, $-13\cos(b(0+c))+7 = -6 \implies \cos(bc)=1 \implies c = 0$.
Final values: $a = -13, b = \pi, c = 0, d = 7$.

Part C: Interval Analysis

(i) At $K$, $h(t)=7$ and is increasing. At $P$, $h(t)=20$ (maximum).
On $(t_1, t_2)$, the height is between $7$ and $20$, so it is positive.
The graph is moving from the midline up to the peak, so it is increasing.
Correct Option: a

(ii) On the interval $(t_1, t_2)$, the graph is concave down as it approaches the maximum.
Therefore, the rate of change of $h$ (the slope) is decreasing.
It starts at its maximum positive value at $K$ and decreases toward zero at $P$.

Question

A windshield wiper blade on a car window rotates back and forth. When the wiper blade is farthest to the left or farthest to the right, the measure of the angle formed by the wiper blade and the vertical centerline (see figure) is (0.75) radians.

At time (t=0) seconds, the wiper blade is farthest to the left. The wiper blade then rotates to the right and passes the vertical centerline. At time (t=1) seconds, the wiper blade is farthest to the right for the first time. Then, the wiper blade rotates left, passes the vertical centerline, and is farthest to the left again at time (t=2) seconds. As the wiper blade rotates, the measure of the angle formed by the wiper blade and the vertical centerline periodically increases and decreases.

The sinusoidal function (h) models the measure of the angle, in radians, formed by the wiper blade and the vertical centerline as a function of time (t), in seconds. A negative value of (h(t)) indicates the wiper blade is to the left of the vertical centerline; a positive value of (h(t)) indicates the wiper blade is to the right of the vertical centerline.

(A) The graph of (h) and its dashed midline for two full cycles is shown. Five points, (F, G, J, K), and (P) are labeled on the graph. No scale is indicated, and no axes are presented. Determine possible coordinates ((t, h(t))) for the five points (F, G, J, K), and (P).

(B) The function (h) can be written in the form (h(t) = a\sin(b(t+c)) + d). Find values of the constants (a, b, c), and (d).

(i) On the interval ((t_1, t_2)), which of the following is true about (h)?

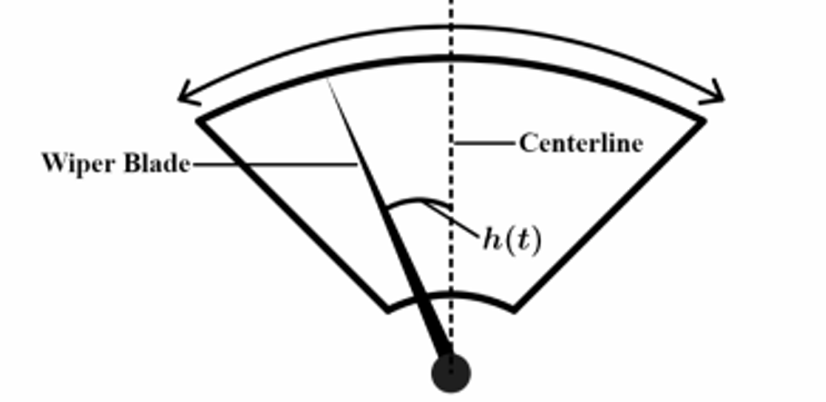
a. (h) is positive and increasing.
b. (h) is positive and decreasing.
c. (h) is negative and increasing.
d. (h) is negative and decreasing.

(ii) Describe how the rate of change of (h) is changing on the interval ((t_1, t_2)).

▶️ Answer/Explanation

Detailed solution

(A) Coordinates for the points (F, G, J, K), and (P)

First, we analyze the motion to establish the timeline:

At (t = 0), the blade is farthest left, so (h(0) = -0.75). This is a minimum value.
At (t = 1), the blade is farthest right, so (h(1) = 0.75). This is a maximum value.
At (t = 2), the blade is farthest left again, so (h(2) = -0.75). This is the next minimum.

The graph shows a sinusoidal wave. Let’s map the points based on this cycle:

Point (F): This is the first maximum peak shown. Since the motion starts at a minimum at (t=0), the first maximum occurs at (t=1).
Coordinate: (F(1, 0.75))
Point (G): This point is on the midline (where (h(t)=0)) as the graph goes downwards from a maximum to a minimum. This occurs exactly halfway between the maximum at (t=1) and the minimum at (t=2).
(t = \frac{1+2}{2} = 1.5).
Coordinate: (G(1.5, 0))
Point (J): This is the minimum trough. We know the minimum occurs at (t=2).
Coordinate: (J(2, -0.75))
Point (K): This point is on the midline as the graph goes upwards from a minimum to the next maximum. This occurs halfway between the minimum at (t=2) and the next maximum at (t=3).
(t = \frac{2+3}{2} = 2.5).
Coordinate: (K(2.5, 0))
Point (P): This is the next maximum peak. The period is (2) seconds (from (t=1) to (t=3)).
Coordinate: (P(3, 0.75))

(B) Finding constants (a, b, c), and (d)

We are fitting the function (h(t) = a\sin(b(t+c)) + d).

Amplitude ((a)): Half the distance between max and min.
(a = \frac{0.75 – (-0.75)}{2} = 0.75).
Vertical Shift ((d)): The average of max and min.
(d = \frac{0.75 + (-0.75)}{2} = 0).
Period ((T)) and Frequency ((b)): The wiper completes a full cycle (left-right-left) in (2) seconds.
(T = 2).
The formula for period is (T = \frac{2\pi}{b}).
(2 = \frac{2\pi}{b} \Rightarrow b = \pi).
Phase Shift ((c)):
We know the function starts at a minimum at (t=0). A standard positive sine wave starts at 0 and goes up. A sine wave shifted to match this graph must cross the midline going upwards at (t=0.5) (halfway between min at (0) and max at (1)).
So, we need the argument of the sine function, (b(t+c)), to be (0) when (t=0.5).
(\pi(0.5 + c) = 0 \Rightarrow c = -0.5).
Alternatively, using (c=1.5) is also valid, but (-0.5) is the simplest magnitude.

Values:
(a = 0.75)
(b = \pi)
(c = -0.5)
(d = 0)

(C) Analysis of interval ((t_1, t_2))

From part (A), (t_1) (point (G)) is (1.5) and (t_2) (point (J)) is (2). The interval is ((1.5, 2)).

(i) Which statement is true?
Looking at the graph between point (G) and point (J):
The graph is below the midline, meaning the values of (h) are negative.
The graph is moving downwards towards the minimum, meaning (h) is decreasing.
Answer: d. (h) is negative and decreasing.

(ii) Rate of change of (h)
The “rate of change of (h)” refers to the derivative, (h'(t)) (the slope of the tangent line).
On the interval ((1.5, 2)), the graph is concave up (it is shaped like a cup).
Mathematically:
– At (G) ((t=1.5)), the slope is at its steepest negative value.
– At (J) ((t=2)), the slope is zero (horizontal tangent at the minimum).
– As the slope goes from a negative number (e.g., (-2)) to (0), the value of the slope is increasing.

Answer: The rate of change of (h) is increasing on the interval ((t_1, t_2)).

Question

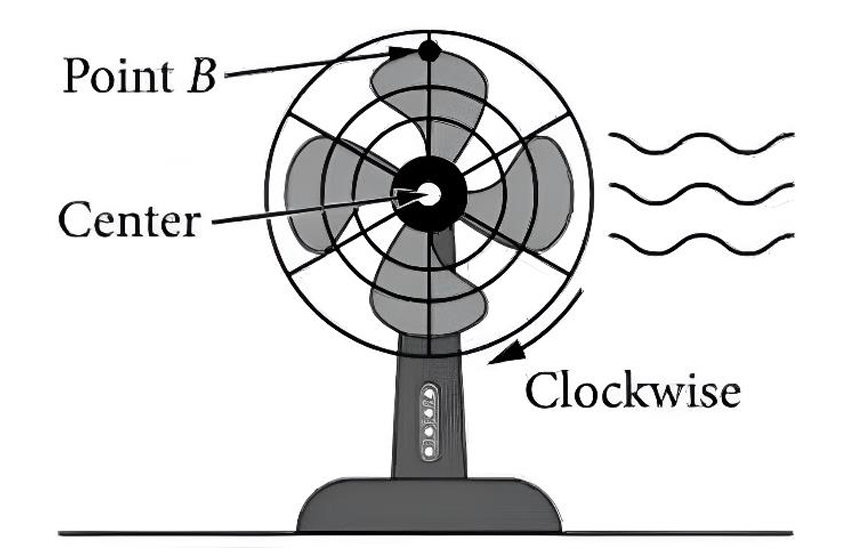
The blades of an electric fan rotate in a clockwise direction and complete $5$ rotations every second. Point $B$ is on the tip of one of the fan blades and is located directly above the center of the fan at time $t = 0$ seconds. Point $B$ is $6$ inches from the center of the fan. The center of the fan is $20$ inches above a level table. The sinusoidal function $h$ models the distance between $B$ and the surface of the table in inches as a function of time $t$ in seconds.

(A) The graph of ℎ and its dashed midline for two full cycles is shown. Five points, 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃 are labeled on the graph. No scale is indicated, and no axes are presented.
Determine the possible coordinates $(t, h(t))$ for the $5$ points: $F, G, J, K,$ and $P$.

(B) The function $h$ can be written in the form $h(t) = a \sin(b(t + c)) + d$. Find values of constants $a, b, c,$ and $d$.

(i) On the interval $(t_1, t_2)$, which of the following is true about $h$?
(A) $h$ is positive and increasing
(B) $h$ is positive and decreasing
(C) $h$ is negative and increasing
(D) $h$ is negative and decreasing

(ii) Describe how the rate of change of $h$ is changing on the interval $(t_1, t_2)$.

▶️ Answer/Explanation

Detailed solution

(A)

The center of the fan is $d = 20$ inches above the table. The radius of the fan blade is $r = 6$ inches, which is the amplitude $a$. The maximum height is $20 + 6 = 26$ inches and the minimum height is $20 – 6 = 14$ inches. The fan completes $5$ rotations per second, so the period is $T = \frac{1}{5} = 0.2$ seconds. Point $B$ starts at the maximum height at $t = 0$, so point $F$ is $(0, 26)$. Point $G$ is at the midline after $\frac{1}{4}$ of a period: $(\frac{0.2}{4}, 20) = (0.05, 20)$. Point $J$ is at the minimum after $\frac{1}{2}$ of a period: $(\frac{0.2}{2}, 14) = (0.1, 14)$. Point $K$ is at the midline after $\frac{3}{4}$ of a period: $(\frac{3 \times 0.2}{4}, 20) = (0.15, 20)$. Point $P$ is at the maximum after $1$ full period: $(0.2, 26)$. The coordinates are: $F(0, 26)$, $G(0.05, 20)$, $J(0.1, 14)$, $K(0.15, 20)$, and $P(0.2, 26)$.

(B)

The amplitude is $a = 6$. The vertical shift (midline) is $d = 20$. The period is $T = 0.2$, so the frequency constant is $b = \frac{2\pi}{0.2} = 10\pi$. Since the function starts at a maximum at $t=0$, it follows $h(t) = 6 \cos(10\pi t) + 20$. To write this as a sine function $h(t) = 6 \sin(10\pi(t + c)) + 20$, we use the identity $\cos(\theta) = \sin(\theta + \frac{\pi}{2})$. Setting $10\pi(t + c) = 10\pi t + \frac{\pi}{2}$, we find $10\pi c = \frac{\pi}{2}$, which gives $c = \frac{1}{20} = 0.05$. Thus, $a = 6$, $b = 10\pi$, $c = 0.05$, and $d = 20$.

(C)

(i) On the interval $(t_1, t_2)$, which is $(0.15, 0.2)$, the graph moves from the midline (point $K$) up to the maximum (point $P$). Throughout this interval, $h(t)$ is between $20$ and $26$, so it is positive. The function is moving upwards, so it is increasing. The correct option is (A) $h$ is positive and increasing.
(ii) On the interval $(t_1, t_2)$, the graph is concave down as it levels off toward the maximum. The slope (rate of change) is positive because the function is increasing. However, the slope is becoming less steep as it approaches the horizontal tangent at point $P$. Therefore, the rate of change of $h$ is decreasing on the interval $(t_1, t_2)$.

AP Precalculus -3.4 Sine and Cosine Graphs- MCQ Exam Style Questions - Effective Fall 2023