AP Precalculus -3.6 Sinusoidal Transformations- Study Notes - Effective Fall 2023
AP Precalculus -3.6 Sinusoidal Transformations- Study Notes – Effective Fall 2023
AP Precalculus -3.6 Sinusoidal Transformations- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify the amplitude, vertical shift, period, and phase shift of a sinusoidal function.
Key Concepts:
- General Form of Sinusoidal Functions
- Vertical (Additive) Transformations of Sinusoidal Functions
Horizontal (Phase) Transformations of Sinusoidal Functions
Vertical (Multiplicative) Transformations of Sinusoidal Functions
Horizontal (Multiplicative) Transformations of Sinusoidal Functions
Key Features of a General Sinusoidal Function
General Form of Sinusoidal Functions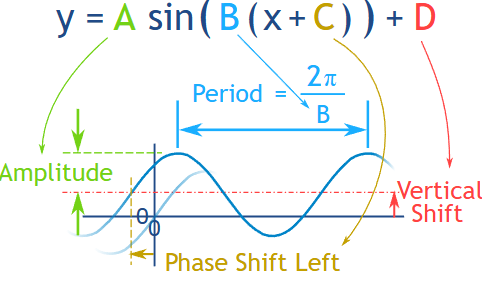
Any function that can be written in the form
\( f(\theta) = a\sin(b(\theta + c)) + d \)
or
\( g(\theta) = a\cos(b(\theta + c)) + d \)
where \( a \), \( b \), \( c \), and \( d \) are real numbers and \( a \ne 0 \), is called a sinusoidal function.
These functions are obtained by applying additive and multiplicative transformations to the basic sine or cosine functions.
Meaning of the Parameters
\( |a| \): amplitude
\( b \): affects the period, where \( \text{Period} = \dfrac{2\pi}{b} \)
\( c \): horizontal (phase) shift
\( d \): vertical shift (midline \( y = d \))
Relationship Between Sine and Cosine
The sine and cosine functions undergo the same types of transformations because the cosine function is simply a phase shift of the sine function.
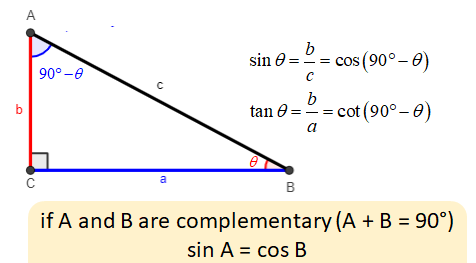
\( \cos \theta = \sin\!\left(\theta – \dfrac{\pi}{2}\right) \)
As a result, any sinusoidal function written using cosine can be rewritten using sine, and vice versa.
Example:
Identify the amplitude, period, phase shift, and midline of the function
\( f(\theta) = 2\sin\!\left(3(\theta – \dfrac{\pi}{6})\right) + 1 \)
▶️ Answer/Explanation
Amplitude:
\( |a| = 2 \)
Period:
\( \dfrac{2\pi}{3} \)
Phase shift:
Right \( \dfrac{\pi}{6} \)
Midline:
\( y = 1 \)
Example:
Rewrite the cosine function
\( g(\theta) = \cos \theta \)
as a sine function.
▶️ Answer/Explanation
Using the phase shift identity,
\( \cos \theta = \sin\!\left(\theta – \dfrac{\pi}{2}\right) \)
This shows that cosine is a horizontally shifted sine function.
Vertical (Additive) Transformations of Sinusoidal Functions
An additive transformation of a sinusoidal function occurs when a constant is added to the function.
For the sine function, consider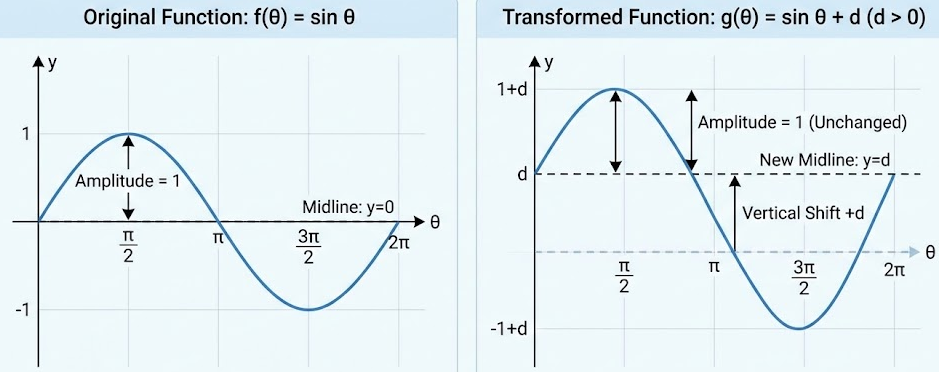
\( f(\theta) = \sin \theta \)
The transformed function
\( g(\theta) = \sin \theta + d \)
is a vertical translation of the graph of \( f \) by \( d \) units.
If \( d > 0 \), the graph shifts upward. If \( d < 0 \), the graph shifts downward.
Effect on the Midline
The midline of \( y = \sin \theta \) is
\( y = 0 \)
After the transformation, the midline becomes
\( y = d \)
The shape, amplitude, and period of the graph remain unchanged.
The same vertical translation applies to the cosine function:
\( g(\theta) = \cos \theta + d \)
This also shifts the graph and its midline by \( d \) units.
Example:
Describe the transformation of the graph of \( y = \sin \theta \) to obtain the graph of
\( y = \sin \theta + 3 \)
▶️ Answer/Explanation
The value \( d = 3 \) represents a vertical translation.
The graph shifts upward by 3 units.
The original midline \( y = 0 \) moves to
\( y = 3 \)
The amplitude and period remain unchanged.
Example:
Identify the midline of the function
\( y = \cos \theta – 2 \)
▶️ Answer/Explanation
The constant \( d = -2 \) shifts the graph downward.
The original midline \( y = 0 \) becomes
\( y = -2 \)
Final answer: The midline is \( y = -2 \).
Horizontal (Phase) Transformations of Sinusoidal Functions
A horizontal transformation, also called a phase shift, occurs when a constant is added to or subtracted from the input of a sinusoidal function.
For the sine function, consider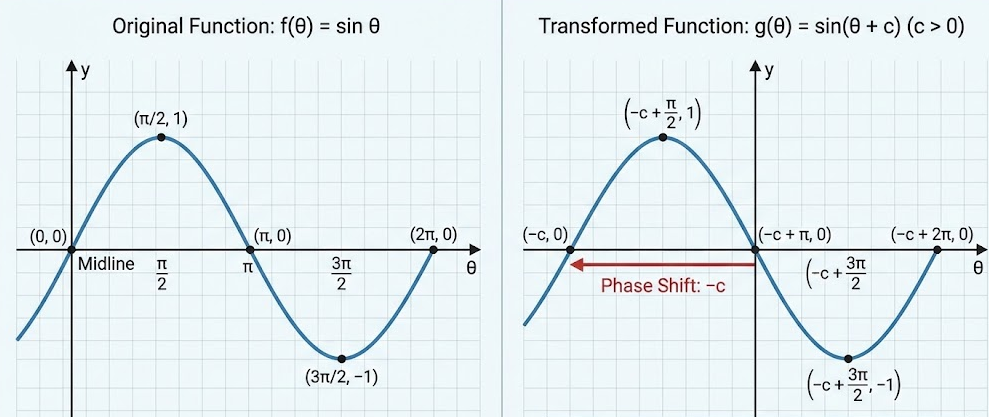
\( f(\theta) = \sin \theta \)
The transformed function
\( g(\theta) = \sin(\theta + c) \)
represents a horizontal translation of the graph of \( f \) by \( -c \) units.
If \( c > 0 \), the graph shifts to the left by \( c \) units. If \( c < 0 \), the graph shifts to the right by \( |c| \) units.
This type of transformation changes the starting position of the wave but does not change its shape.
Effect on Key Features
Amplitude: unchanged
Period: unchanged
Midline: unchanged
The same horizontal translation applies to the cosine function:
\( g(\theta) = \cos(\theta + c) \)
This shifts the graph of \( y = \cos \theta \) by \( -c \) units as well.
Example:
Describe the transformation of the graph of \( y = \sin \theta \) to obtain the graph of
\( y = \sin(\theta + \dfrac{\pi}{3}) \)
▶️ Answer/Explanation
Here, \( c = \dfrac{\pi}{3} \).
The graph is shifted horizontally by \( -\dfrac{\pi}{3} \).
This means the graph shifts left by \( \dfrac{\pi}{3} \).
All other features remain the same.
Example:
Identify the phase shift of the function
\( y = \cos(\theta – \dfrac{\pi}{4}) \)
▶️ Answer/Explanation
The expression can be written as \( \cos(\theta + c) \) with \( c = -\dfrac{\pi}{4} \).
The horizontal shift is \( -c = \dfrac{\pi}{4} \).
Final answer: The graph shifts right by \( \dfrac{\pi}{4} \).
Vertical (Multiplicative) Transformations of Sinusoidal Functions
A multiplicative transformation of a sinusoidal function occurs when the entire function is multiplied by a constant.
For the sine function, consider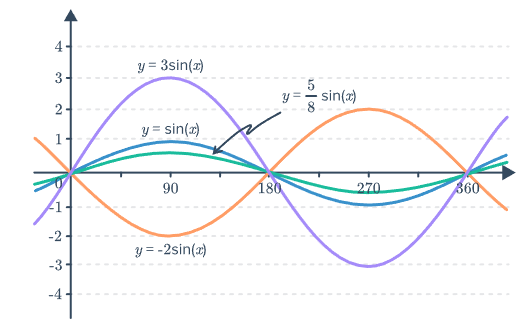
\( f(\theta) = \sin \theta \)
The transformed function
\( g(\theta) = a\sin \theta \)
is a vertical dilation of the graph of \( f \).
The amplitude of the graph is multiplied by a factor of \( |a| \).
If \( |a| > 1 \), the graph is vertically stretched. If \( 0 < |a| < 1 \), the graph is vertically compressed.
If \( a < 0 \), the graph is also reflected across the midline.
The same vertical dilation applies to the cosine function:
\( g(\theta) = a\cos \theta \)
This transformation changes the amplitude but does not affect the period or midline.
Example:
Describe the effect of the transformation
\( y = 3\sin \theta \)
▶️ Answer/Explanation
The value \( a = 3 \).
The graph is vertically stretched by a factor of 3.
The amplitude changes from 1 to 3.
The midline and period remain unchanged.
Example:
Find the amplitude of the function
\( y = -\dfrac{1}{2}\cos \theta \)
▶️ Answer/Explanation
The amplitude is the absolute value of the coefficient.
\( \text{Amplitude} = \left| -\dfrac{1}{2} \right| = \dfrac{1}{2} \)
The negative sign indicates a reflection across the midline.
Final answer: The amplitude is \( \dfrac{1}{2} \).
Horizontal (Multiplicative) Transformations of Sinusoidal Functions
A multiplicative transformation applied to the input of a sinusoidal function affects the horizontal scaling of its graph.
For the sine function, consider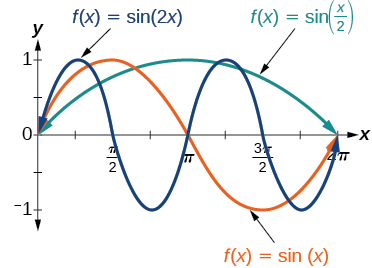
\( f(\theta) = \sin \theta \)
The transformed function
\( g(\theta) = \sin(b\theta) \)
is a horizontal dilation (or compression) of the graph of \( f \).
This transformation changes the period of the function.
Effect on the Period
The period of \( y = \sin \theta \) is \( 2\pi \).
For \( y = \sin(b\theta) \), the new period is
\( \text{Period} = \dfrac{2\pi}{|b|} \)
Thus, the period differs from the original by a factor of
\( \left| \dfrac{1}{b} \right| \)
If \( |b| > 1 \), the graph is horizontally compressed. If \( 0 < |b| < 1 \), the graph is horizontally stretched.
The amplitude and midline remain unchanged.
The same horizontal dilation applies to the cosine function:
\( g(\theta) = \cos(b\theta) \)
Example:
Describe the effect of the transformation
\( y = \sin(3\theta) \)
▶️ Answer/Explanation
Here, \( b = 3 \).
The new period is
\( \dfrac{2\pi}{3} \)
The graph is horizontally compressed by a factor of \( \dfrac{1}{3} \).
The amplitude and midline remain the same.
Example:
Find the period of the function
\( y = \cos\!\left(\dfrac{1}{2}\theta\right) \)
▶️ Answer/Explanation
Here, \( b = \dfrac{1}{2} \).
Use the period formula:
\( \text{Period} = \dfrac{2\pi}{\frac{1}{2}} = 4\pi \)
Final answer: The period is \( 4\pi \).
Key Features of a General Sinusoidal Function
Consider the sinusoidal function
\( y = f(\theta) = a\sin(b(\theta + c)) + d \)
This function is a transformation of the basic sine function and has several important characteristics that describe its graph.
Amplitude
The amplitude is the maximum distance the graph moves away from its midline.
Amplitude: \( |a| \)
Period
The period is the length of one complete cycle of the graph.
Period: \( \left| \dfrac{1}{b} \right| 2\pi = \dfrac{2\pi}{|b|} \)
Midline (Vertical Shift)
The midline is the horizontal line about which the graph oscillates.
Midline: \( y = d \)
This represents a vertical shift of \( d \) units from the line \( y = 0 \).
Phase Shift
The phase shift describes the horizontal translation of the graph.
Phase shift: \( -c \)
If \( c > 0 \), the graph shifts left. If \( c < 0 \), the graph shifts right.
The same interpretations apply to the cosine function
\( y = a\cos(b(\theta + c)) + d \)
because cosine is a phase shift of sine.
Example:
Identify the amplitude, period, midline, and phase shift of the function
\( y = -3\sin\!\left(2(\theta + \dfrac{\pi}{4})\right) + 1 \)
▶️ Answer/Explanation
Amplitude:
\( |a| = 3 \)
Period:
\( \dfrac{2\pi}{2} = \pi \)
Midline:
\( y = 1 \)
Phase shift:
\( -\dfrac{\pi}{4} \), which is a shift left by \( \dfrac{\pi}{4} \)
Example:
State the key features of the cosine function
\( y = 2\cos\!\left(\dfrac{1}{3}(\theta – \pi)\right) – 4 \)
▶️ Answer/Explanation
Amplitude:
\( 2 \)
Period:
\( \dfrac{2\pi}{\frac{1}{3}} = 6\pi \)
Midline:
\( y = -4 \)
Phase shift:
Right \( \pi \)
