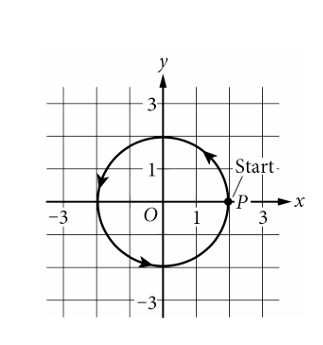
AP Precalculus -3.7 Sinusoidal Modeling- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.7 Sinusoidal Modeling- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.7 Sinusoidal Modeling- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The table gives ordered pairs for five points from a larger data set. The larger data set can be modeled by a sinusoidal function $f$ with a period of 4. The maximum values of the data set occur at $x$-values that are multiples of 4. Which of the following best defines $f(x)$ for the larger data set?

(A) $\cos\left(\frac{\pi}{2}x\right) + 4$
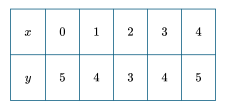
(B) $\cos(\pi x) + 4$
(C) $2\cos\left(\frac{\pi}{2}x\right) + 4$
(D) $2\cos(\pi x) + 4$

▶️ Answer/Explanation

Detailed solution

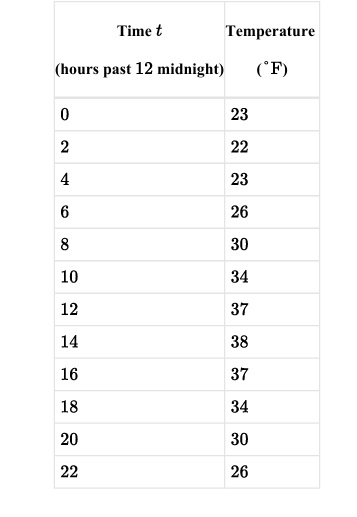
From the table:
Max value $y=5$ at $x=0,4$ (multiples of 4)
Min value $y=3$ at $x=2$
Midline: $ \frac{5+3}{2} = 4 $
Amplitude: $ \frac{5-3}{2} = 1 $
Period = 4 → $ \frac{2\pi}{b} = 4 $ → $ b = \frac{\pi}{2} $
Using cosine with max at $x=0$: $ f(x) = 1\cdot \cos\left(\frac{\pi}{2}x\right) + 4 $
✅ Answer: (A)

Question

A table gives temperatures in degrees Fahrenheit in a town on a given day. The sinusoidal function $ F(t) = 8 \cos \left( \frac{\pi}{12} (t + c) \right) + 30 $ models the data, where $ t $ is hours past midnight. Which of the following is true about the value of $ c $?

(A) The value of $ c $ is $ 2 $ because this accounts for a phase shift that aligns a minimum value of the data set with a minimum value of $ F $.
(B) The value of $ c $ is $ 2 $ because this accounts for a vertical shift that aligns a minimum value of the data set with a minimum value of $ F $.
(C) The value of $ c $ is $ 14 $ because this accounts for a phase shift that aligns a maximum value of the data set with a maximum value of $ F $.
(D) The value of $ c $ is $ 14 $ because this accounts for a vertical shift that aligns a maximum value of the data set with a maximum value of $ F $.

▶️ Answer/Explanation

Detailed solution

Step 1: Identify key features of the data

From the table, the maximum temperature is $38^\circ\mathrm{F}$ at $t = 14$,
and the minimum temperature is $22^\circ\mathrm{F}$ at $t = 2$.

Step 2: Interpret the sinusoidal model

The model is $F(t) = 8\cos\left(\dfrac{\pi}{12}(t + c)\right) + 30$.

The amplitude is $8$, the midline is $30$, and the period is
$\dfrac{2\pi}{\pi/12} = 24$ hours, which matches a daily temperature cycle.

Step 3: Use the cosine maximum

A cosine function reaches its maximum when its argument is $0$.
Thus, the maximum of $F$ occurs when
$\dfrac{\pi}{12}(t + c) = 0$, which gives $t + c = 0$.

Step 4: Align the maximum of the model with the data

The data show a maximum temperature at $t = 14$.
Substituting gives $14 + c = 0$, so $c = -14$.

Since cosine is periodic, a phase shift of $-14$ is equivalent to $14$.
Thus, $c = 14$.

Step 5: Interpret the meaning of $c$

The constant $c$ appears inside the cosine function, so it represents a
phase shift. The value $c = 14$ aligns a maximum of the model with a
maximum of the data.

$\boxed{\text{Correct answer: (C)}}$

Question

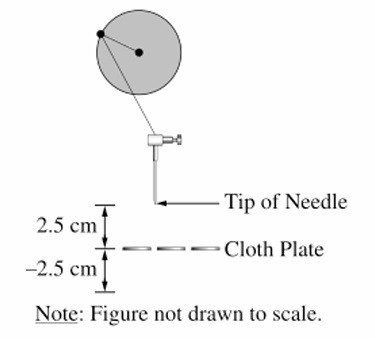
The vertical motion of the tip of a needle on a sewing machine is periodic with respect to time and can be modeled by a sinusoidal function. The figure shows the location of the tip of the needle in relation to a cloth plate. The tip of the needle moves straight up and down above and below the cloth plate. The table gives a consecutive maximum and minimum displacement of the tip at two times. The function $ d $ models the displacement, in centimeters, of the tip of the needle from the cloth plate at time $ t $, in seconds. Which of the following expressions could define $ d(t) $?

Time $ t $ (seconds)	Displacement (cm)
0	2.5
1/24	–2.5

(A) $ 2.5 \cos\left(\frac{1}{12}t\right) $
(B) $ 2.5 \cos\left(\frac{\pi}{6}t\right) $
(C) $ 2.5 \cos(24\pi t) $
(D) $ 2.5 \cos(48\pi t) $

▶️ Answer/Explanation

Detailed solution

From the table: at $ t = 0 $, displacement = $ 2.5 $ cm (maximum); at $ t = \frac{1}{24} $ s, displacement = $ -2.5 $ cm (minimum).
Amplitude $ A = \frac{2.5 – (-2.5)}{2} = 2.5 $ cm.
The time from a maximum to the next minimum is half the period, so $ T/2 = \frac{1}{24} $ ⇒ $ T = \frac{1}{12} $ seconds.
For $ d(t) = A\cos(bt) $, the period is $ T = \frac{2\pi}{b} $.
Set $ \frac{2\pi}{b} = \frac{1}{12} $ ⇒ $ b = 24\pi $.
Thus $ d(t) = 2.5\cos(24\pi t) $, which matches choice (C).
✅ Answer: (C)

Question

In the tidal area of a certain city, a sinusoidal function $ f(x) = a \sin(b(x + c)) + d $, where $ a, b, c, $ and $ d $ are constants, is used to model one cycle of high and low tides. The maximum value of the tide is 8.88 feet, and the minimum value of the tide is 0.54 feet in that cycle. If the values of $ b, c, $ and $ d $ have already been determined to fit the data, which of the following would best define $ f(x) $?

(A) $ 4.17 \sin(b(x + c)) + d $
(B) $ 4.44 \sin(b(x + c)) + d $
(C) $ 4.71 \sin(b(x + c)) + d $
(D) $ 8.34 \sin(b(x + c)) + d $

▶️ Answer/Explanation

Detailed solution

Amplitude $ a $ is half the difference between the maximum and minimum:
$ a = \frac{8.88 – 0.54}{2} = \frac{8.34}{2} = 4.17 $.
Thus the function is $ f(x) = 4.17 \sin(b(x + c)) + d $.
✅ Answer: (A)

Question

The table gives the maximum temperature in degrees Celsius on the first day of each of nine months. The function $ f(\theta) = a \sin(b(\theta + c)) + d $ models these data with period 12 months. Based on the table, which is the best value for $ d $?

Month $\theta$	1	2	3	4	5	6	7	8	9
Temp (°C)	6.1	-5.5	-6.0	10.0	17.2	25.6	30.6	32.2	26.1

(A) $ \frac{\pi}{6} $
(B) 13
(C) 19
(D) 38

▶️ Answer/Explanation

Detailed solution

The parameter $ d $ represents the vertical shift (midline) of the sinusoidal model, which is the average of the maximum and minimum temperatures in the data.
Maximum temperature = 32.2°C, Minimum temperature = -6.0°C.
Midline $ d = \frac{32.2 + (-6.0)}{2} = \frac{26.2}{2} = 13.1 \approx 13 $.
✅ Answer: (B)

Question

The height of point $ P $ is given by $ h(t) = 6 + 6\cos\left(\frac{\pi}{3}t\right) $ inches. If the child rides for 5 minutes (300 seconds), how many times will point $ P $ touch the ground?

(A) 1
(B) 50
(C) 100
(D) 286

▶️ Answer/Explanation

Detailed solution

Ground level corresponds to $ h(t) = 0 $.
The minimum of $ h(t) $ occurs when $ \cos\left(\frac{\pi}{3}t\right) = -1 $, giving $ h_{\min} = 6 + 6(-1) = 0 $.
Thus $ P $ touches ground once per period when $\cos = -1$.
Period $ T = \frac{2\pi}{\pi/3} = 6 $ seconds.
Number of periods in 300 seconds: $ \frac{300}{6} = 50 $.
So $ P $ touches ground 50 times.
✅ Answer: (B)

Question

Part of a video game design involves the use of one period of a sinusoidal function as the path that a spaceship will follow across a rectangular video screen. The video screen has a width of 1000 pixels and a height of 600 pixels. The values $ x = 0 $ and $ x = 1000 $ represent the left and right sides of the screen, respectively. The values $ y = 0 $ and $ y = 600 $ represent the bottom and top sides of the screen, respectively.

The path of the spaceship begins on the left side of the screen, $ x = 0 $, and completes one period of a sinusoidal function by ending on the right side of the screen, $ x = 1000 $. During its path, the spaceship reaches its minimum height of $ y = 200 $ before reaching its maximum height of $ y = 500 $. If $ y = f(x) $ models the path of the spaceship, which of the following could define $ f(x) $?

(A) $-300 \sin \left( \frac{\pi}{500} x \right) + 350$
(B) $-150 \sin \left( \frac{\pi}{500} x \right) + 350$
(C) $ 150 \sin \left( \frac{\pi}{500} x \right) + 350$
(D) $ 300 \sin \left( \frac{\pi}{500} x \right) + 350$

▶️ Answer/Explanation

Detailed solution

Midline: $ \frac{500 + 200}{2} = 350 $.
Amplitude: $ \frac{500 – 200}{2} = 150 $.
Period = 1000 ⇒ $ \frac{2\pi}{b} = 1000 $ ⇒ $ b = \frac{\pi}{500} $.

Since the ship hits the minimum before the maximum, the sine wave is inverted relative to $ \sin x $ (which goes from 0 up to max first).
So we use $ -A \sin(bx) + k $.
Thus $ f(x) = -150 \sin\left( \frac{\pi}{500} x \right) + 350 $.

✅ Answer: (B)

Question

The amount of water is modeled by $g(t)=5\sin(0.8(t+2))+25$. It was determined that the model underestimates the amount by $800$ gallons (8 hundreds). Which function is a better model?

(A) $f(t)=5\sin(0.8(t+10))+25$
(B) $h(t)=5\sin(0.8(t+2))+33$
(C) $k(t)=5\sin(6.4(t+2))+25$
(D) $m(t)=40\sin(0.8(t+2))+25$

▶️ Answer/Explanation

Detailed solution

1. Identify the Adjustment:
The current model underestimates by 800 gallons. Since units are in hundreds, we must add $8$ to the output.

2. Adjust the Function:
New Function $= g(t) + 8 = [5\sin(0.8(t+2))+25] + 8 = 5\sin(0.8(t+2)) + 33$.

✅ Answer: (B)

Question

A physical therapy center has a bicycle that patients use for exercise. The height, in inches (in), of the bicycle pedal above level ground periodically increases and decreases when used. The figure gives the position of the pedal $ P $ at a height of 12 inches above the ground at time $ t = 0 $ seconds. The pedal’s 8-inch arm defines the circular motion of the pedal. If a patient pedals 1 revolution per second, which of the following could be an expression for $ h(t) $, the height, in inches, of the bicycle pedal above level ground at time $ t $ seconds?

(A) $ 8 – 12\sin t $
(B) $ 12 – 8\sin t $
(C) $ 8 – 12\sin(2\pi t) $
(D) $ 12 – 8\sin(2\pi t) $

▶️ Answer/Explanation

Detailed solution

The pedal moves in a circle with radius $8$ inches, so the amplitude is $8$.
At time $t = 0$, the pedal is $12$ inches above the ground, so the midline is $12$.

Thus, the height function has the form
$h(t) = 12 \pm 8(\text{trigonometric function})$.

The patient pedals $1$ revolution per second, so the period is $1$ second.
This corresponds to an angular frequency of $2\pi$.

Therefore, the function must involve $\sin(2\pi t)$.

At $t = 0$, the pedal height is $12$.
Since $\sin 0 = 0$,

$h(0) = 12 – 8\sin(2\pi \cdot 0) = 12$,

which matches the given condition.

$\boxed{\text{Correct answer: (D)}}$

$h(t) = 12 – 8\sin(2\pi t)$

Question

At a coastal city, the height of the tide, in feet (ft), is modeled by the function $ h $, defined by $ h(t) = 6.3 \cos\left(\frac{\pi}{6} t\right) + 7.5 $ for $ 0 \leq t \leq 12 $ hours. Based on the model, which of the following is true?

(A) The maximum height of the tide is 13.8 ft.
(B) The maximum height of the tide occurs at $ t = 6 $ hours.
(C) The minimum height of the tide is 1 ft.
(D) The minimum height of the tide occurs at $ t = 12 $ hours.

▶️ Answer/Explanation

Detailed solution

$ h(t) = 6.3\cos\left(\frac{\pi}{6} t\right) + 7.5 $.
Amplitude = 6.3, midline = 7.5.
Max when $\cos = 1$: $ h_{\text{max}} = 6.3 + 7.5 = 13.8 $ ft.
Min when $\cos = -1$: $ h_{\text{min}} = -6.3 + 7.5 = 1.2 $ ft.
Max occurs when $\frac{\pi}{6} t = 0, 2\pi, \dots$ ⇒ $ t = 0, 12, \dots $.
Min occurs when $\frac{\pi}{6} t = \pi$ ⇒ $ t = 6 $.
Thus (A) is true.
✅ Answer: (A)

Question

A large wheel of radius 2 feet is rotated at a constant rate. At time $ t = 0 $ minutes, the wheel begins to rotate. Point $ P $ on the wheel is at the “Start” position. At time $ t = 20 $ minutes, 120 rotations of the wheel have been completed, and $ P $ is in the same position as it was at time $ t = 0 $. A sinusoidal function is used to model the y-coordinate of the position of $ P $ as a function of time $ t $ in minutes. Which of the following functions is an appropriate model for this situation?

(A) $ f(t) = 2\sin\left(\frac{\pi}{10}t\right) $
(B) $ f(t) = 2\sin\left(\frac{\pi}{3}t\right) $
(C) $ f(t) = 2\sin(6t) $
(D) $ f(t) = 2\sin(12\pi t) $

▶️ Answer/Explanation

Detailed solution

Given: 120 rotations in 20 minutes ⇒ frequency = $ \frac{120}{20} = 6 $ rotations per minute.
Period = $ \frac{1}{\text{frequency}} = \frac{1}{6} $ minute.
Sinusoidal model for y-coordinate: $ f(t) = a\sin(bt) $ with amplitude $ a = 2 $ (radius).
Period formula: $ \frac{2\pi}{b} = \frac{1}{6} $ ⇒ $ b = 12\pi $.
Thus, $ f(t) = 2\sin(12\pi t) $.
Check: At $ t = 0 $, $ f(0) = 0 $ (assuming start at y=0). After $ t = 1/6 $ minute, one full cycle occurs.
✅ Answer: (D)

Question

A Ferris wheel has a diameter of $30$ meters and sits $15$ meters off the ground on its lowest point. The Ferris wheel makes $2$ rotations per minute and spins counterclockwise. At $t = 0$, Jeremy is in a carriage at the bottom of the Ferris wheel. After $4$ minutes and $25$ seconds, how far is Jeremy off the ground?

a. $22.5$ meters
b. $44.5$ meters
c. $17.0$ meters
d. $30.0$ meters

▶️ Answer/Explanation

Detailed solution

The radius of the wheel is $r = \frac{30}{2} = 15$ meters, and the center is at $h_c = 15 + 15 = 30$ meters.
The wheel completes $2$ rotations per minute, meaning it takes $30$ seconds for one full rotation.
The total time elapsed is $4$ minutes and $25$ seconds, which equals $265$ seconds.
The number of rotations is $\frac{265}{30} = 8$ full rotations plus $\frac{25}{30} = \frac{5}{6}$ of a rotation.
A $\frac{5}{6}$ rotation starting from the bottom ($270^\circ$) ends at $270^\circ + (\frac{5}{6} \times 360^\circ) = 570^\circ$, which is equivalent to $210^\circ$.
At $210^\circ$ (or $30^\circ$ below the horizontal), the vertical displacement from the center is $15 \sin(-30^\circ) = -7.5$ meters.
The final height off the ground is $30 – 7.5 = 22.5$ meters.
Therefore, the correct option is a.

Question

The number of people waiting in a line to enter a stadium can be modeled by function $ b $ defined by $ b(t) = 42 \cos\left(\frac{\pi}{30}t\right) + 45 $ for $ 0 \le t \le 60 $, where $ t $ is the time, in minutes, since the stadium opened. Based on the graph of the model, which of the following is true?

(A) The number of people in line is never equal to 0 because the midline vertical shift is greater than the amplitude

(B) The number of people in line is never equal to 0 because the amplitude is greater than the midline vertical shift

(D) The number of people in line reaches 0 because the amplitude is greater than the midline vertical shift

▶️ Answer/Explanation

Detailed solution

The given function is $ b(t) = 42 \cos\left(\frac{\pi}{30}t\right) + 45 $.
Identify the midline vertical shift, which is the constant term: $ 45 $.
Identify the amplitude, which is the coefficient of the cosine function: $ 42 $.
The minimum value of the function occurs when the cosine term is $ -1 $.
Minimum number of people $ = \text{Midline} – \text{Amplitude} = 45 – 42 = 3 $.
Since the minimum value ($ 3 $) is greater than $ 0 $, the line never reaches $ 0 $.
This happens specifically because the vertical shift ($ 45 $) is larger than the amplitude ($ 42 $).
Therefore, option (A) is the correct answer.

Question

Ayan Prashar from the foot star system was found alive, in a crashed space vehicle. A medical team is monitoring his body temperature, using the function $ B $ given by

$ B(t) = 115 + 9 \cos \left[ \frac{1}{20} (t + 12\pi) \right] $

Where $ t $ is the time, in minutes, since they started monitoring Ayan for $ 0 \le t \le 120 $. Which of the following best describes the behavior of $ B(t) $, when $ t = 60 $ minutes?

(A) Ayan’s body temperature is increasing at an increasing rate.

(B) Ayan’s body temperature is increasing at a decreasing rate.

(D) Ayan’s body temperature is decreasing at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

To determine the behavior, we calculate the first derivative $ B'(t) $ (rate of change) and the second derivative $ B”(t) $ (rate of the rate).
$ B'(t) = \frac{d}{dt}\left(115 + 9\cos\left[\frac{t+12\pi}{20}\right]\right) = -\frac{9}{20}\sin\left(\frac{t+12\pi}{20}\right) $
$ B”(t) = \frac{d}{dt}\left(B'(t)\right) = -\frac{9}{400}\cos\left(\frac{t+12\pi}{20}\right) $
At $ t = 60 $, the angle is $ \theta = \frac{60+12\pi}{20} = 3 + 0.6\pi \approx 4.88 $ radians. Since $ \frac{3\pi}{2} \approx 4.71 < 4.88 < 2\pi $, the angle is in the 4th Quadrant.
In Q4, sine is negative and cosine is positive. Therefore:
$ B'(60) = -\text{ve} \times \sin(\text{Q4}) = -\text{ve} \times (-\text{ve}) = \text{Positive} $ (Temperature is increasing).
$ B”(60) = -\text{ve} \times \cos(\text{Q4}) = -\text{ve} \times (+\text{ve}) = \text{Negative} $ (Rate is decreasing).
Thus, the temperature is increasing at a decreasing rate.

Correct Option: (B)

Question

A physical therapy center has a bicycle that patients use for exercise. The height, in inches (in), of the bicycle pedal above level ground periodically increases and decreases when used. The figure gives the position of the pedal $P$ at a height of 12 inches above the ground at time $t = 0$ seconds. The pedal’s 8-inch arm defines the circular motion of the pedal. If a patient pedals 1 revolution per second, which of the following could be an expression for $h(t)$, the height, in inches, of the bicycle pedal above level ground at time $t$ seconds?

(A) $ 8 – 12 \sin t $

(B) $ 12 – 8 \sin t $

(D) $ 12 – 8 \sin(2\pi t) $

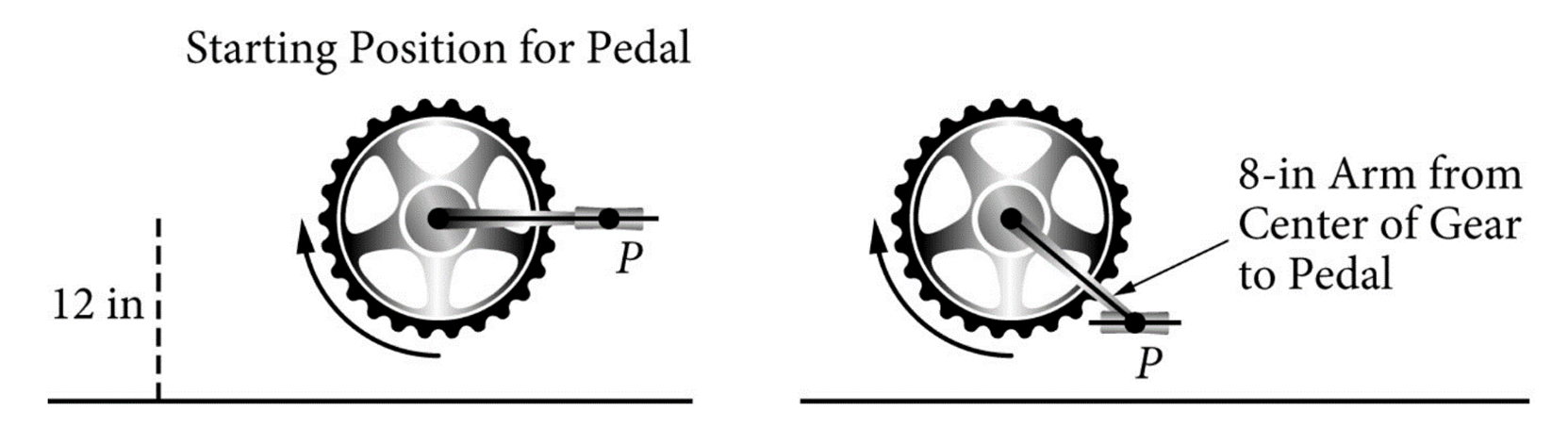
▶️ Answer/Explanation

Detailed solution

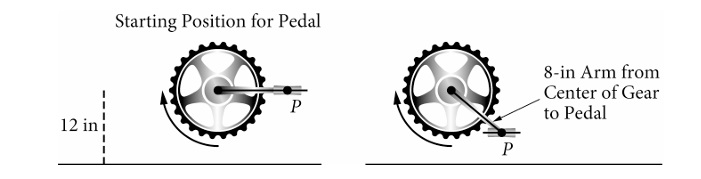
The center of the gear is 12 inches above the ground, so the vertical midline of the function is 12.
The length of the pedal arm is 8 inches, which determines the amplitude of the motion, so amplitude = 8.
The pedal completes 1 revolution per second, meaning the period $T = 1$.
The coefficient of $t$ inside the function is determined by $\frac{2\pi}{T} = \frac{2\pi}{1} = 2\pi$.
At $t=0$, the pedal starts at the midline (12 in) and moves clockwise (downwards first).
A sine function starts at the midline; since it moves down first, it must be a negative sine function.
Combining these components gives the expression: $h(t) = 12 – 8 \sin(2\pi t)$.

Correct Option: (D)

Question

The number of minutes of daylight per day for a certain city can be modeled by the function $ D $ given by $ D(t) = 160 \cos\left(\frac{2\pi}{365}(t – 172)\right) + 729 $, where $ t $ is the day of the year for $ 1 \le t \le 365 $. Which of the following best describes the behavior of $ D(t) $ on day $ 150 $?

(A) The number of minutes of daylight per day is increasing at a decreasing rate.

(B) The number of minutes of daylight per day is decreasing at a decreasing rate.

(D) The number of minutes of daylight per day is decreasing at an increasing rate.

▶️ Answer/Explanation

Detailed solution

To determine the behavior, we examine the first derivative (slope) and second derivative (concavity) at $ t = 150 $.

1. Determine if increasing or decreasing:
Calculate $ D'(t) = -160\left(\frac{2\pi}{365}\right)\sin\left(\frac{2\pi}{365}(t – 172)\right) $. At $ t = 150 $, the term $ (t-172) $ is negative. Since sine is an odd function, the sine term is negative. Multiplying by the negative coefficient makes $ D'(150) $ positive. Thus, daylight is increasing.

2. Determine the rate of change:
Calculate $ D”(t) = -160\left(\frac{2\pi}{365}\right)^2\cos\left(\frac{2\pi}{365}(t – 172)\right) $. At $ t = 150 $, the cosine of a small angle is positive. The leading negative sign makes $ D”(150) $ negative. This means the graph is concave down, or the rate is decreasing.

Conclusion: The function is increasing at a decreasing rate. (Option A)

Question

The height of a point on a dolphin swimming in the ocean can be modeled by a sinusoidal function $h$. For time $t$, in seconds, if $h(t)$ is positive, the point on the dolphin is above the surface of the water, and if $h(t)$ is negative, the point on the dolphin is below the surface of the water. As the dolphin swims, it jumps to a maximum height of $3$ feet above the surface, then hits the surface, and dives to a minimum height of $3$ feet below the surface. The dolphin then returns to the surface, and jumps to a maximum height of $3$ feet above the surface. This cycle from maximum height to the next maximum height repeats every $4$ seconds. Which of the following could be an expression for $h(t)$?

(A) $3 \sin\left(\frac{\pi}{2}t\right)$

(B) $3 \sin(\pi t)$

(D) $\sin(\pi t) + 3$

▶️ Answer/Explanation

Detailed solution

The maximum height is $3$ and minimum is $-3$, so the amplitude $A = 3$.
The centerline is the water surface, so the vertical shift $D = 0$.
The period $P$ is given as $4$ seconds.
The value of $b$ in the expression $\sin(bt)$ is calculated as $b = \frac{2\pi}{P}$.
Substituting the period: $b = \frac{2\pi}{4} = \frac{\pi}{2}$.
Combining these values, the function takes the form $h(t) = 3 \sin\left(\frac{\pi}{2}t\right)$.
Therefore, the correct choice is (A).

Question

The average monthly high temperature, in degrees Fahrenheit ($^\circ\text{F}$), varies periodically for a certain city. The table gives the average monthly high temperature for selected months of the year. Based on a sinusoidal regression of these data, a model is constructed to predict average monthly high temperature as a function of time $t$, the number of the month of the year. What is the average monthly high temperature predicted by the model for June ($t = 6$)?

(A) $53.7^\circ\text{F}$

(B) $61.8^\circ\text{F}$

(D) $65.3^\circ\text{F}$

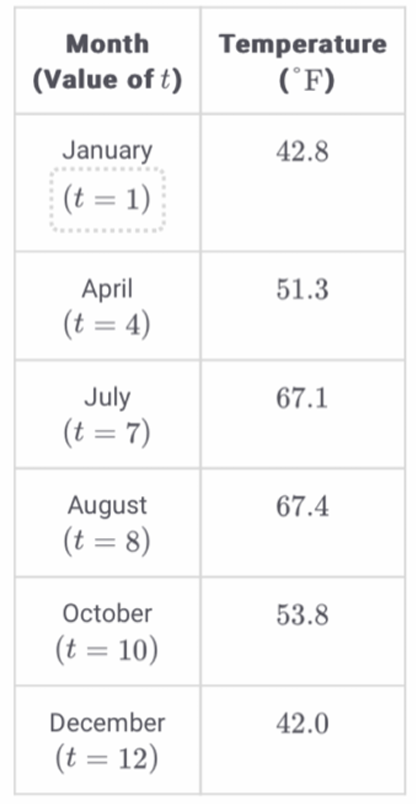
▶️ Answer/Explanation

Detailed solution

The correct answer is (C).
Input the given $(t, \text{Temp})$ pairs into a graphing calculator’s sinusoidal regression ($SinReg$) tool.
The resulting model is approximately $y = 12.87\sin(0.50t – 2.19) + 54.89$.
Substitute $t = 6$ into the regression equation to find the temperature for June.
Ensure the calculator is in Radian mode for the calculation.
The predicted temperature is $54.89 + 12.87\sin(0.50(6) – 2.19) \approx 64.88$.
Rounding to the nearest tenth gives $64.9^\circ\text{F}$.

Question

The average daily temperature, in degrees Fahrenheit ($^\circ\text{F}$), in a certain city can be modeled by the function $f$ given by $f(t) = 63.6 + 21.9 \sin\left(\frac{2\pi}{365}(t – c)\right)$, where $t$ is the number of days since the beginning of the year and $c$ is a constant. January $1$ corresponds to $t = 1$. On January $10$ ($t = 10$), the average temperature was $41.7^\circ\text{F}$. Based on the model, what is the predicted average temperature on February $28$ ($t = 59$)?

(A) $49.040^\circ\text{F}$
(B) $52.057^\circ\text{F}$
(C) $52.650^\circ\text{F}$
(D) $82.211^\circ\text{F}$

▶️ Answer/Explanation

Detailed solution

Set up the initial equation: $41.7 = 63.6 + 21.9 \sin\left(\frac{2\pi}{365}(10 – c)\right)$.
Isolate the sine term: $\sin\left(\frac{2\pi}{365}(10 – c)\right) = \frac{41.7 – 63.6}{21.9} = -1$.
Find the argument: $\frac{2\pi}{365}(10 – c) = \arcsin(-1) = -\frac{\pi}{2}$.
Solve for the constant $c$: $10 – c = -\frac{365}{4}$, which gives $c = 101.25$.
Substitute $t = 59$ and $c$ into the model: $f(59) = 63.6 + 21.9 \sin\left(\frac{2\pi}{365}(59 – 101.25)\right)$.
Calculate the value: $f(59) = 63.6 + 21.9 \sin(-0.7275 \text{ radians}) \approx 52.057$.
The predicted average temperature is approximately $52.057^\circ\text{F}$.
Therefore, the correct option is (B).

Question

A second hand on a clock rotates clockwise at a constant speed around the clock. However, Charlie bought a new clock that is dysfunctional, where the second hand completes a cycle every (30) seconds. The clock is (24) inches in diameter and is (5) feet above the ground. The distance between the point at which the second hand is pointing to and the ground is periodically increasing and decreasing. The second hand starts at (t = 0) pointing straight up towards the number (12).

(A) This situation can be represented with a sinusoidal function in the form $h(t) = a \cos( b(t + c) ) + d$, where $t$ is the number of seconds after starting the clock and $h(t)$ is the height of the end of the second hand in inches. Find the function.

(B) When does the arrow of the second hand become $72 – 6\sqrt{2}$ inches above the ground on the interval $0 < t \leq 30$?

(C) i. Between $0 \leq t \leq 30$, does the graph of $h(t)$ have a point of inflection? If so, identify all the points of inflection between the time intervals. If it does not, explain why using your knowledge of a cosine function and its continuity.

ii. Explain the meaning of these points in context of the problem using the definition of the rate of change and the rate the rate is changing.

Most-appropriate topic codes (CED):

• TOPIC 3.7: Sinusoidal Function Context and Data Modeling — part (A)
• TOPIC 3.10: Trigonometric Equations and Inequalities — part (B)
• TOPIC 1.1: Change in Tandem — part (C)

▶️ Answer/Explanation

Detailed solution

(A)
First, determine the physical parameters of the clock to find the sinusoidal constants.
The diameter is (24) inches, so the radius is (12) inches. This corresponds to the amplitude, (a = 12).
The center of the clock is (5) feet above the ground, which converts to (60) inches. This is the midline, (d = 60).
The second hand completes a cycle every (30) seconds. The period is (30), so the frequency coefficient is (b = \dfrac{2\pi}{30} = \dfrac{\pi}{15}).
At (t = 0), the hand is pointing straight up (maximum height). Since the cosine function starts at a maximum, there is no phase shift, so (c = 0).
Thus, the function is:
(h(t) = 12 \cos\left( \dfrac{\pi}{15} t \right) + 60)

(B)
Set $h(t)$ equal to the given height and solve for $t$:
$12 \cos\left( \dfrac{\pi}{15} t \right) + 60 = 72 – 6\sqrt{2}$
$12 \cos\left( \dfrac{\pi}{15} t \right) = 12 – 6\sqrt{2}$
$\cos\left( \dfrac{\pi}{15} t \right) = 1 – \dfrac{\sqrt{2}}{2} = \dfrac{2 – \sqrt{2}}{2}$
Let $\theta = \dfrac{\pi}{15} t$. We need to solve $\cos \theta = \dfrac{2 – \sqrt{2}}{2}$.
$\theta = \pm \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right) + 2\pi k$.
For the interval $0 < t \leq 30$, we look for solutions in $(0, 2\pi]$.
The two solutions for $\theta$ are $\theta_1 = \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right)$ and $\theta_2 = 2\pi – \theta_1$.
Converting back to time $t = \dfrac{15}{\pi} \theta$:
$t_1 = \dfrac{15}{\pi} \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right)$ and $t_2 = 30 – t_1$.

(C) i.
Yes, the graph of $h(t)$ has points of inflection. The function $h(t)$ is a smooth, continuous cosine wave.
Points of inflection on a sinusoidal graph occur where the graph crosses its midline (concavity changes from up to down or vice versa). This happens when:
$\cos\left( \dfrac{\pi}{15} t \right) = 0$
$\dfrac{\pi}{15} t = \dfrac{\pi}{2} + k\pi$
$t = 15\left( \dfrac{1}{2} + k \right) = 7.5 + 15k$
For the interval $0 \leq t \leq 30$:
If $k=0$, $t = 7.5$.
If $k=1$, $t = 22.5$.
The points of inflection are at $t = 7.5$ seconds and $t = 22.5$ seconds.

(C) ii.
In this context:
The rate of change represents the vertical velocity of the tip of the second hand.
The rate the rate is changing represents the vertical acceleration.
A point of inflection occurs where the concavity changes, which means the vertical acceleration is transitioning from positive to negative (or vice versa) and is instantaneously zero. Physically, these are the moments when the tip of the second hand is at the same height as the center of the clock (midline). At these specific points, the vertical speed (rate of change) is at its absolute maximum magnitude.

Question

(B) When does the arrow of the second hand become $72 – 6\sqrt{2}$ inches above the ground on the interval $0 < t \leq 30$?

ii. Explain the meaning of these points in context of the problem using the definition of the rate of change and the rate the rate is changing.

Most-appropriate topic codes (CED):

▶️ Answer/Explanation

Detailed solution

Question

The figure shows a robotic arm rotating in a circular counterclockwise direction that completes one rotation every $2$ seconds. Point $S$ is on the tip of the arm, and point $X$ does not move. As the arm rotates at a constant speed, the height of $S$ above $X$ periodically increases and decreases. At time $t = 0$ seconds, $S$ is at its lowest position, $6$ inches directly below $X$. At its highest position, $S$ is $20$ inches directly above $X$.

The sinusoidal function $h$ models the height of $S$ above $X$, in inches, as a function of time $t$, in seconds. A positive value of $h(t)$ indicates $S$ is above $X$; a negative value of $h(t)$ indicates $S$ is below $X$.

Part A
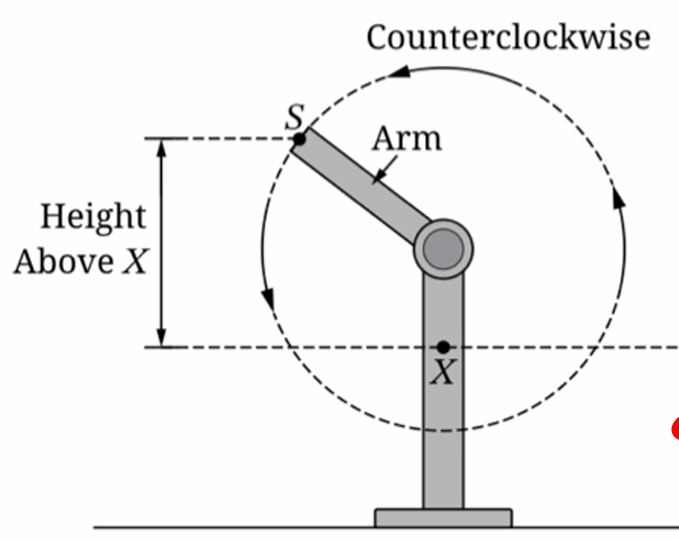
The graph of $h$ and its dashed midline for two full cycles is shown. Five points, $F, G, J, K,$ and $P$, are labeled on the graph. Determine possible coordinates $(t, h(t))$ for the five points.

Part B
The function $h$ can be written in the form $h(t) = a \cos(b(t + c)) + d$. Find values of constants $a, b, c,$ and $d$.

Part C
Refer to the graph of $h$ in part (A). The $t$-coordinate of $K$ is $t_1$, and the $t$-coordinate of $P$ is $t_2$.
(i) On the interval $(t_1, t_2)$, which of the following is true about $h$?
a. $h$ is positive and increasing.
b. $h$ is positive and decreasing.
c. $h$ is negative and increasing.
d. $h$ is negative and decreasing.
(ii) Describe how the rate of change of $h$ is changing on the interval $(t_1, t_2)$.

▶️ Answer/Explanation

Detailed solution

Part A: Coordinates of Points

At $t = 0$, $S$ is at its minimum height $-6$ (below $X$).
The maximum height is $20$.
The midline $d = \frac{20 + (-6)}{2} = 7$.
The period is $2$ seconds.
The graph starts at a minimum at $t = 0$, reaches midline at $t = 0.5$, maximum at $t = 1$, midline at $t = 1.5$, and minimum at $t = 2$.
Based on the visual positions in the provided graph:
$F$ (first maximum): $(1, 20)$
$G$ (midline, decreasing): $(1.5, 7)$
$J$ (minimum): $(2, -6)$
$K$ (midline, increasing): $(2.5, 7)$
$P$ (second maximum): $(3, 20)$

Part B: Finding Constants

$a$ (Amplitude) $= \frac{20 – (-6)}{2} = 13$. Since we use $\cos$ and start at a minimum, $a = -13$ (or use a phase shift).
$d$ (Vertical shift/Midline) $= 7$.
$b$ (Frequency factor) $= \frac{2\pi}{\text{period}} = \frac{2\pi}{2} = \pi$.
$c$ (Phase shift): For $h(t) = a \cos(b(t+c)) + d$, if $a = -13$, then at $t=0$, $-13\cos(b(0+c))+7 = -6 \implies \cos(bc)=1 \implies c = 0$.
Final values: $a = -13, b = \pi, c = 0, d = 7$.

Part C: Interval Analysis

(i) At $K$, $h(t)=7$ and is increasing. At $P$, $h(t)=20$ (maximum).
On $(t_1, t_2)$, the height is between $7$ and $20$, so it is positive.
The graph is moving from the midline up to the peak, so it is increasing.
Correct Option: a

(ii) On the interval $(t_1, t_2)$, the graph is concave down as it approaches the maximum.
Therefore, the rate of change of $h$ (the slope) is decreasing.
It starts at its maximum positive value at $K$ and decreases toward zero at $P$.

Question

A windshield wiper blade on a car window rotates back and forth. When the wiper blade is farthest to the left or farthest to the right, the measure of the angle formed by the wiper blade and the vertical centerline (see figure) is (0.75) radians.

At time (t=0) seconds, the wiper blade is farthest to the left. The wiper blade then rotates to the right and passes the vertical centerline. At time (t=1) seconds, the wiper blade is farthest to the right for the first time. Then, the wiper blade rotates left, passes the vertical centerline, and is farthest to the left again at time (t=2) seconds. As the wiper blade rotates, the measure of the angle formed by the wiper blade and the vertical centerline periodically increases and decreases.

The sinusoidal function (h) models the measure of the angle, in radians, formed by the wiper blade and the vertical centerline as a function of time (t), in seconds. A negative value of (h(t)) indicates the wiper blade is to the left of the vertical centerline; a positive value of (h(t)) indicates the wiper blade is to the right of the vertical centerline.

(A) The graph of (h) and its dashed midline for two full cycles is shown. Five points, (F, G, J, K), and (P) are labeled on the graph. No scale is indicated, and no axes are presented. Determine possible coordinates ((t, h(t))) for the five points (F, G, J, K), and (P).

(B) The function (h) can be written in the form (h(t) = a\sin(b(t+c)) + d). Find values of the constants (a, b, c), and (d).

(i) On the interval ((t_1, t_2)), which of the following is true about (h)?

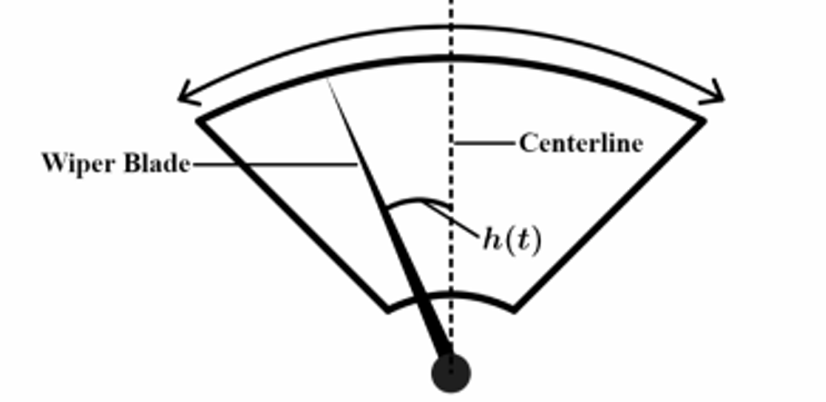
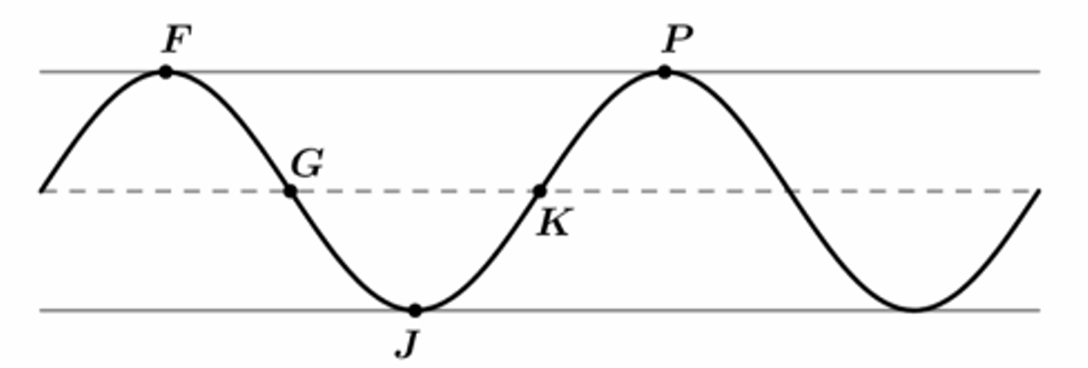
a. (h) is positive and increasing.
b. (h) is positive and decreasing.
c. (h) is negative and increasing.
d. (h) is negative and decreasing.

(ii) Describe how the rate of change of (h) is changing on the interval ((t_1, t_2)).

▶️ Answer/Explanation

Detailed solution

(A) Coordinates for the points (F, G, J, K), and (P)

First, we analyze the motion to establish the timeline:

At (t = 0), the blade is farthest left, so (h(0) = -0.75). This is a minimum value.
At (t = 1), the blade is farthest right, so (h(1) = 0.75). This is a maximum value.
At (t = 2), the blade is farthest left again, so (h(2) = -0.75). This is the next minimum.

The graph shows a sinusoidal wave. Let’s map the points based on this cycle:

Point (F): This is the first maximum peak shown. Since the motion starts at a minimum at (t=0), the first maximum occurs at (t=1).
Coordinate: (F(1, 0.75))
Point (G): This point is on the midline (where (h(t)=0)) as the graph goes downwards from a maximum to a minimum. This occurs exactly halfway between the maximum at (t=1) and the minimum at (t=2).
(t = \frac{1+2}{2} = 1.5).
Coordinate: (G(1.5, 0))
Point (J): This is the minimum trough. We know the minimum occurs at (t=2).
Coordinate: (J(2, -0.75))
Point (K): This point is on the midline as the graph goes upwards from a minimum to the next maximum. This occurs halfway between the minimum at (t=2) and the next maximum at (t=3).
(t = \frac{2+3}{2} = 2.5).
Coordinate: (K(2.5, 0))
Point (P): This is the next maximum peak. The period is (2) seconds (from (t=1) to (t=3)).
Coordinate: (P(3, 0.75))

(B) Finding constants (a, b, c), and (d)

We are fitting the function (h(t) = a\sin(b(t+c)) + d).

Amplitude ((a)): Half the distance between max and min.
(a = \frac{0.75 – (-0.75)}{2} = 0.75).
Vertical Shift ((d)): The average of max and min.
(d = \frac{0.75 + (-0.75)}{2} = 0).
Period ((T)) and Frequency ((b)): The wiper completes a full cycle (left-right-left) in (2) seconds.
(T = 2).
The formula for period is (T = \frac{2\pi}{b}).
(2 = \frac{2\pi}{b} \Rightarrow b = \pi).
Phase Shift ((c)):
We know the function starts at a minimum at (t=0). A standard positive sine wave starts at 0 and goes up. A sine wave shifted to match this graph must cross the midline going upwards at (t=0.5) (halfway between min at (0) and max at (1)).
So, we need the argument of the sine function, (b(t+c)), to be (0) when (t=0.5).
(\pi(0.5 + c) = 0 \Rightarrow c = -0.5).
Alternatively, using (c=1.5) is also valid, but (-0.5) is the simplest magnitude.

Values:
(a = 0.75)
(b = \pi)
(c = -0.5)
(d = 0)

(C) Analysis of interval ((t_1, t_2))

From part (A), (t_1) (point (G)) is (1.5) and (t_2) (point (J)) is (2). The interval is ((1.5, 2)).

(i) Which statement is true?
Looking at the graph between point (G) and point (J):
The graph is below the midline, meaning the values of (h) are negative.
The graph is moving downwards towards the minimum, meaning (h) is decreasing.
Answer: d. (h) is negative and decreasing.

(ii) Rate of change of (h)
The “rate of change of (h)” refers to the derivative, (h'(t)) (the slope of the tangent line).
On the interval ((1.5, 2)), the graph is concave up (it is shaped like a cup).
Mathematically:
– At (G) ((t=1.5)), the slope is at its steepest negative value.
– At (J) ((t=2)), the slope is zero (horizontal tangent at the minimum).
– As the slope goes from a negative number (e.g., (-2)) to (0), the value of the slope is increasing.

Answer: The rate of change of (h) is increasing on the interval ((t_1, t_2)).

Question

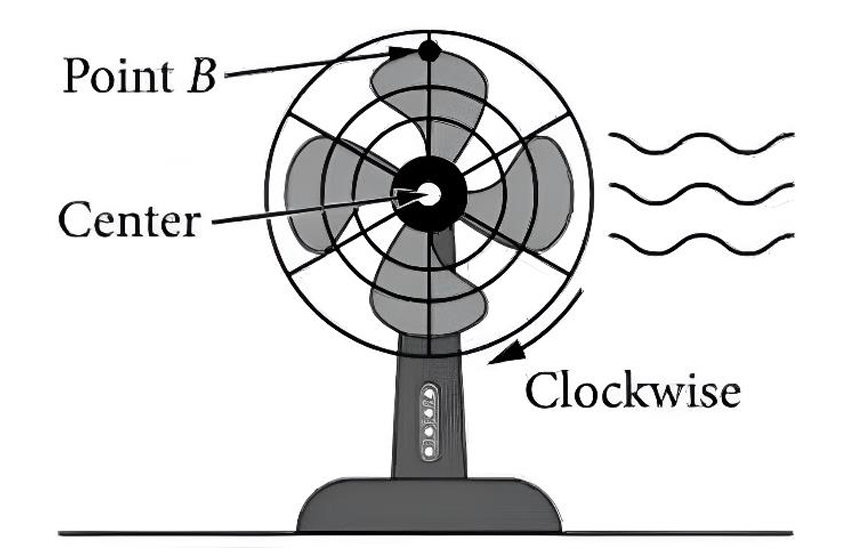
The blades of an electric fan rotate in a clockwise direction and complete $5$ rotations every second. Point $B$ is on the tip of one of the fan blades and is located directly above the center of the fan at time $t = 0$ seconds. Point $B$ is $6$ inches from the center of the fan. The center of the fan is $20$ inches above a level table. The sinusoidal function $h$ models the distance between $B$ and the surface of the table in inches as a function of time $t$ in seconds.

(A) The graph of ℎ and its dashed midline for two full cycles is shown. Five points, 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃 are labeled on the graph. No scale is indicated, and no axes are presented.
Determine the possible coordinates $(t, h(t))$ for the $5$ points: $F, G, J, K,$ and $P$.

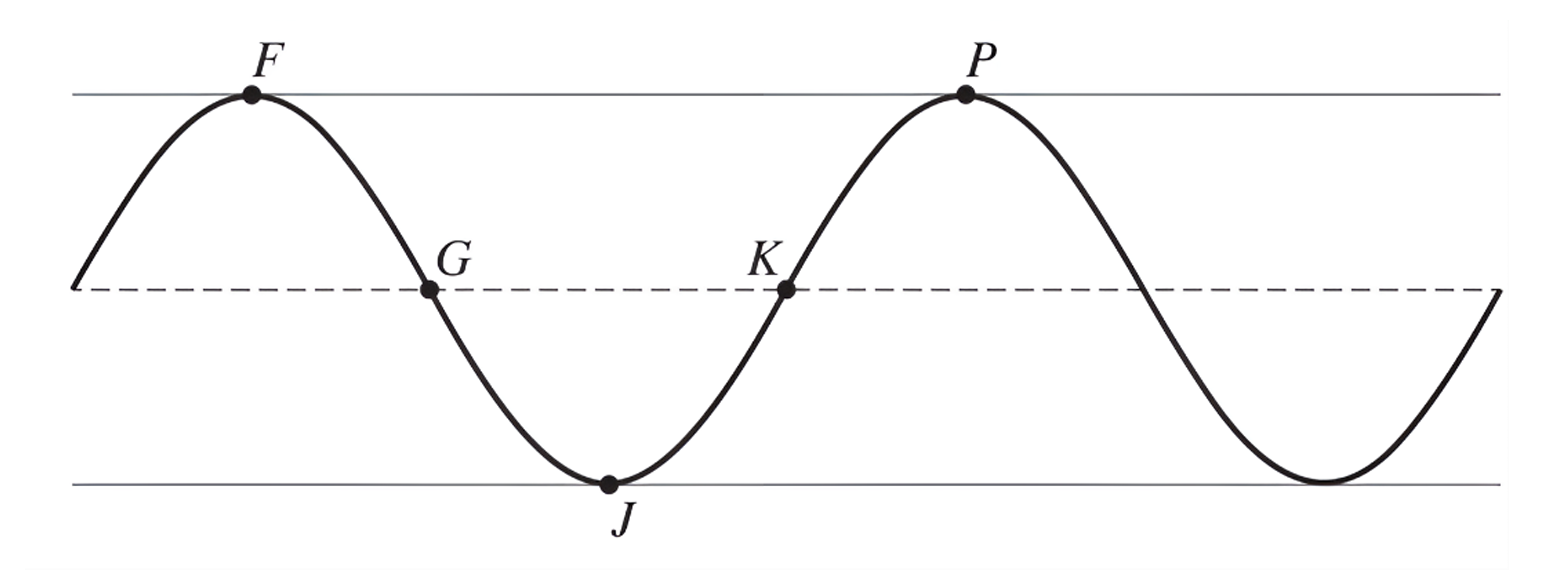
(B) The function $h$ can be written in the form $h(t) = a \sin(b(t + c)) + d$. Find values of constants $a, b, c,$ and $d$.

(i) On the interval $(t_1, t_2)$, which of the following is true about $h$?
(A) $h$ is positive and increasing
(B) $h$ is positive and decreasing
(C) $h$ is negative and increasing
(D) $h$ is negative and decreasing

(ii) Describe how the rate of change of $h$ is changing on the interval $(t_1, t_2)$.

▶️ Answer/Explanation

Detailed solution

(A)

The center of the fan is $d = 20$ inches above the table. The radius of the fan blade is $r = 6$ inches, which is the amplitude $a$. The maximum height is $20 + 6 = 26$ inches and the minimum height is $20 – 6 = 14$ inches. The fan completes $5$ rotations per second, so the period is $T = \frac{1}{5} = 0.2$ seconds. Point $B$ starts at the maximum height at $t = 0$, so point $F$ is $(0, 26)$. Point $G$ is at the midline after $\frac{1}{4}$ of a period: $(\frac{0.2}{4}, 20) = (0.05, 20)$. Point $J$ is at the minimum after $\frac{1}{2}$ of a period: $(\frac{0.2}{2}, 14) = (0.1, 14)$. Point $K$ is at the midline after $\frac{3}{4}$ of a period: $(\frac{3 \times 0.2}{4}, 20) = (0.15, 20)$. Point $P$ is at the maximum after $1$ full period: $(0.2, 26)$. The coordinates are: $F(0, 26)$, $G(0.05, 20)$, $J(0.1, 14)$, $K(0.15, 20)$, and $P(0.2, 26)$.

(B)

The amplitude is $a = 6$. The vertical shift (midline) is $d = 20$. The period is $T = 0.2$, so the frequency constant is $b = \frac{2\pi}{0.2} = 10\pi$. Since the function starts at a maximum at $t=0$, it follows $h(t) = 6 \cos(10\pi t) + 20$. To write this as a sine function $h(t) = 6 \sin(10\pi(t + c)) + 20$, we use the identity $\cos(\theta) = \sin(\theta + \frac{\pi}{2})$. Setting $10\pi(t + c) = 10\pi t + \frac{\pi}{2}$, we find $10\pi c = \frac{\pi}{2}$, which gives $c = \frac{1}{20} = 0.05$. Thus, $a = 6$, $b = 10\pi$, $c = 0.05$, and $d = 20$.

(C)

(i) On the interval $(t_1, t_2)$, which is $(0.15, 0.2)$, the graph moves from the midline (point $K$) up to the maximum (point $P$). Throughout this interval, $h(t)$ is between $20$ and $26$, so it is positive. The function is moving upwards, so it is increasing. The correct option is (A) $h$ is positive and increasing.
(ii) On the interval $(t_1, t_2)$, the graph is concave down as it levels off toward the maximum. The slope (rate of change) is positive because the function is increasing. However, the slope is becoming less steep as it approaches the horizontal tangent at point $P$. Therefore, the rate of change of $h$ is decreasing on the interval $(t_1, t_2)$.

AP Precalculus -3.7 Sinusoidal Modeling- MCQ Exam Style Questions - Effective Fall 2023