AP Precalculus -3.8 The Tangent Function- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.8 The Tangent Function- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.8 The Tangent Function- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

Which of the following describes the graph of $ f(x) = \cot x $?

(A) The graph has vertical asymptotes at $ x = \frac{\pi}{2} + n\pi $, where $ k $ is any integer, and the function is increasing on all intervals in its domain.
(B) The graph has vertical asymptotes at $ x = \frac{\pi}{2} + n\pi $, where $ k $ is any integer, and the function is decreasing on all intervals in its domain.
(C) The graph has vertical asymptotes at $ x = \pi + n\pi $, where $ k $ is any integer, and the function is increasing on all intervals in its domain.
(D) The graph has vertical asymptotes at $ x = \pi + n\pi $, where $ k $ is any integer, and the function is decreasing on all intervals in its domain.

▶️ Answer/Explanation

Detailed solution

$ f(x) = \cot x = \frac{\cos x}{\sin x} $.
Vertical asymptotes occur where $ \sin x = 0 $ → $ x = 0 + n\pi = n\pi $ (or $ x = \pi + n\pi $ is same as $ x = n\pi $ if $ n $ starts from 0). In list form: $ x = k\pi $ for integer $ k $. Option (D) says $ x = \pi + n\pi $, which is equivalent if $ n $ ranges over all integers.
Cotangent is decreasing on each interval $ (k\pi, (k+1)\pi) $.
Thus (D) matches: asymptotes at $ x = \pi + n\pi $ (i.e., $ k\pi $) and decreasing.
✅ Answer: (D)

Question

Which of the following is the graph of $ f(x) = 3\sin(2x) $ in the $ xy $-plane?

Key features of $ f(x) = 3\sin(2x) $:
Amplitude = 3, Period = $ \frac{2\pi}{2} = \pi $.
Graph passes through origin, oscillates between $ y = 3 $ and $ y = -3 $, completes one full cycle from $ x = 0 $ to $ x = \pi $.

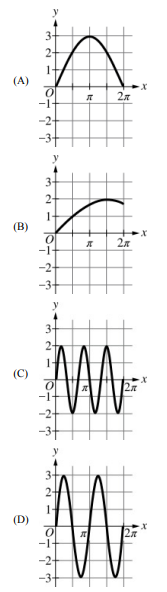
▶️ Answer/Explanation

Detailed solution

$ f(x) = 3\sin(2x) $ has:
Amplitude $ = 3 $, period $ = \frac{2\pi}{2} = \pi $.
The graph starts at $ (0,0) $, increases to a maximum at $ x = \frac{\pi}{4} $, returns to 0 at $ x = \frac{\pi}{2} $, reaches a minimum at $ x = \frac{3\pi}{4} $, and returns to 0 at $ x = \pi $.
Among the options, the correct graph shows this behavior with amplitude 3 and period $ \pi $.
✅ Answer: (D)

Question

The function $ g $ is given by $ g(\theta) = \tan(2\pi\theta) $. Which of the following statements about the graph of $ g $ in the $ xy $-plane is true?

(A) The vertical asymptotes occur at $ \theta = 0 + \frac{1}{2}k $, where $ k $ is an integer.
(B) The vertical asymptotes occur at $ \theta = \frac{1}{4} + \frac{1}{2}k $, where $ k $ is an integer.
(C) The vertical asymptotes occur at $ \theta = \frac{1}{4} + k $, where $ k $ is an integer.
(D) The vertical asymptotes occur at $ \theta = \frac{1}{2} + 2k $, where $ k $ is an integer.

▶️ Answer/Explanation

Detailed solution

For $ g(\theta) = \tan(2\pi\theta) $, the period is $ \frac{\pi}{2\pi} = \frac{1}{2} $.
Vertical asymptotes occur where $ \cos(2\pi\theta) = 0 $, i.e., where $ 2\pi\theta = \frac{\pi}{2} + \pi k $.
Solving: $ \theta = \frac{1}{4} + \frac{1}{2}k $, where $ k $ is an integer.
✅ Answer: (B)

Question

The function $j$ is given by $j(x) = 8 – 7 \tan \left(\frac{x}{4}\right)$. Which of the following gives the vertical asymptotes of $j$?

(A) $x = \frac{\pi}{2} + \pi k$, where $k$ is an integer

(B) $x = \frac{\pi}{8} + \frac{\pi}{4} k$, where $k$ is an integer

(D) $x = 4\pi + 8\pi k$, where $k$ is an integer

▶️ Answer/Explanation

Detailed solution

The standard tangent function, $y = \tan(\theta)$, has vertical asymptotes when $\theta = \frac{\pi}{2} + \pi k$, where $k$ is an integer.
For the given function $j(x) = 8 – 7 \tan\left(\frac{x}{4}\right)$, the argument of the tangent is $\frac{x}{4}$.
To find the vertical asymptotes, we set the argument equal to the asymptotic values: $\frac{x}{4} = \frac{\pi}{2} + \pi k$.
Now, solve for $x$ by multiplying both sides of the equation by $4$.

$x = 4\left(\frac{\pi}{2}\right) + 4(\pi k)$

Simplifying the expression gives $x = 2\pi + 4\pi k$.
Therefore, the vertical asymptotes occur at $x = 2\pi + 4\pi k$, where $k$ is an integer.

Correct Option: (C)

Question

The figure shows the graph of $ f(x) = a \tan(bx) $, where $ a $ and $ b $ are constants, in the $ xy $-plane. The graph of $ f $ has two vertical asymptotes at $ x = -\pi $ and $ x = \pi $, and a point with coordinates $ (2.317, 1.829) $. What are all solutions of $ f(x) = 1.829 $?

(A) $ x = 2.317 $ only

(B) $ x = 2.317 + \pi k $, where $ k $ is any integer

(D) $ x = 2.317 + 3\pi k $, where $ k $ is any integer

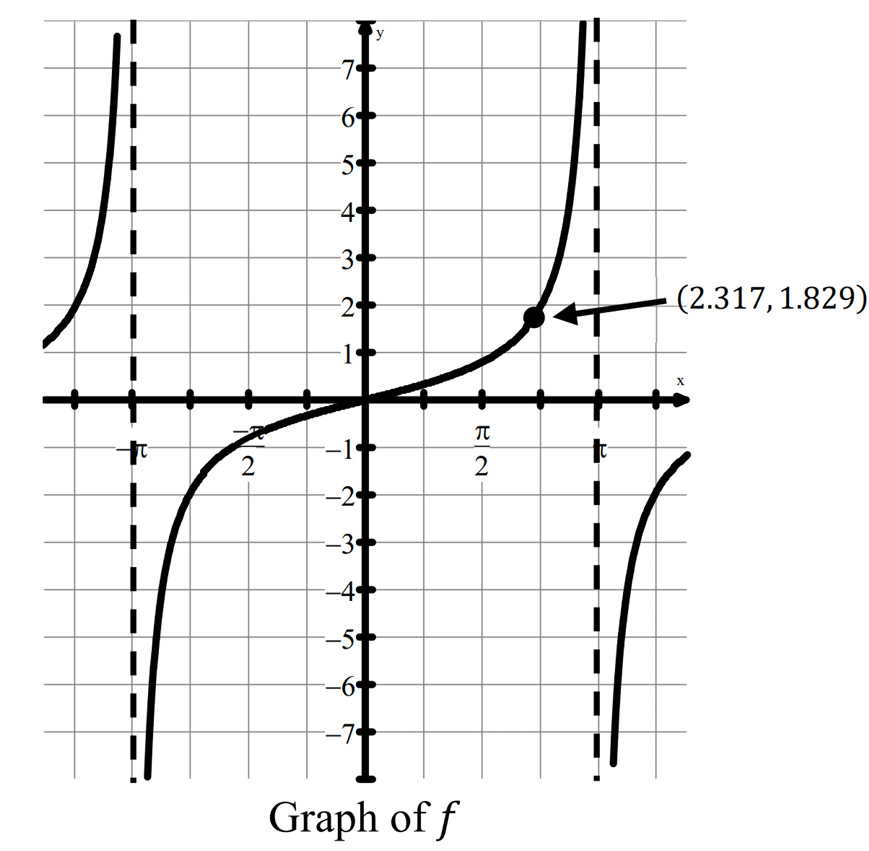
▶️ Answer/Explanation

Detailed solution

The correct option is (C).

The period of a tangent function is determined by the horizontal distance between consecutive vertical asymptotes.
From the given graph, the vertical asymptotes are located at $ x = -\pi $ and $ x = \pi $.
Therefore, the period of the function $ f(x) $ is the difference: $ \pi – (-\pi) = 2\pi $.
We are given a specific point on the curve where $ f(2.317) = 1.829 $, meaning $ x = 2.317 $ is one valid solution.
Since the tangent function is periodic, the values of $ f(x) $ repeat every period.
Thus, the general solution for $ f(x) = 1.829 $ is the initial x-value plus integer multiples of the period.
This gives the expression: $ x = 2.317 + 2\pi k $, where $ k $ is any integer.

Question

The function $ h $ is given by $ h(\theta) = \tan(3\theta) + 1 $. Which of the following statements about the graph of $ h $ in the $ xy $-plane is true?

(A) The vertical asymptotes of the graph of $ h $ occur at input values $ \theta = \frac{\pi}{6} + \frac{\pi}{6}k $, where $ k $ is an integer

(B) The vertical asymptotes of the graph of $ h $ occur at input values $ \theta = \frac{\pi}{6} + \frac{\pi}{3}k $, where $ k $ is an integer

(C) The vertical asymptotes of the graph of $ h $ occur at input values $ \theta = \frac{\pi}{3} + \frac{\pi}{6}k $, where $ k $ is an integer

(D) The vertical asymptotes of the graph of $ h $ occur at input values $ \theta = \frac{\pi}{3} + \frac{\pi}{3}k $, where $ k $ is an integer

▶️ Answer/Explanation

Detailed solution

The standard tangent function, $ y = \tan(x) $, has vertical asymptotes where the function is undefined, which is at $ x = \frac{\pi}{2} + \pi k $ for any integer $ k $.
For the function $ h(\theta) = \tan(3\theta) + 1 $, the argument is $ 3\theta $.
We set the argument equal to the asymptotic condition: $ 3\theta = \frac{\pi}{2} + \pi k $.
Solving for $ \theta $, we divide the entire equation by 3: $ \theta = \frac{1}{3}(\frac{\pi}{2} + \pi k) $.
This simplifies to $ \theta = \frac{\pi}{6} + \frac{\pi}{3}k $.
Comparing this result with the given options, it corresponds to statement (B).

Question

In the $xy$-plane, angle $BAC$ is an angle in standard position with terminal ray $AC$, which intersects the unit circle at the point with coordinates $(0.4, -0.9)$. Which of the following descriptions is correct?

(A) The tangent of angle $BAC$ is $-\frac{4}{9}$, and the slope of ray $AC$ is $-\frac{4}{9}$.
(B) The tangent of angle $BAC$ is $-\frac{4}{9}$, and the slope of ray $AC$ is $-\frac{9}{4}$.
(C) The tangent of angle $BAC$ is $-\frac{9}{4}$, and the slope of ray $AC$ is $-\frac{9}{4}$.
(D) The tangent of angle $BAC$ is $-\frac{9}{4}$, and the slope of ray $AC$ is $\frac{4}{9}$.

▶️ Answer/Explanation

Detailed solution

The terminal ray $AC$ passes through the origin $(0,0)$ and the point $(0.4, -0.9)$.
The slope of ray $AC$ is calculated as $m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{-0.9 – 0}{0.4 – 0} = -\frac{0.9}{0.4}$.
Simplifying the slope gives $m = -\frac{9}{4}$.
For an angle $\theta$ in standard position, $\tan(\theta) = \frac{y}{x}$ where $(x, y)$ is a point on the terminal ray.
Thus, $\tan(BAC) = \frac{-0.9}{0.4} = -\frac{9}{4}$.
Both the tangent of the angle and the slope of the ray are equal to $-\frac{9}{4}$.
Therefore, the correct description is given in option (C).

Question

An angle $\theta$ is in standard position in the $xy$-plane. Which of the following is true about $\theta$ on the interval $0 \le \theta \le 2\pi$ if $\tan \theta = 1$?

(A) There is a value of $\theta$ on $0 \le \theta \le 2\pi$ for which $\tan \theta = 1$ in Quadrant I only.
(B) There are values of $\theta$ on $0 \le \theta \le 2\pi$ for which $\tan \theta = 1$ in Quadrants I and III only.
(C) There are values of $\theta$ on $0 \le \theta \le 2\pi$ for which $\tan \theta = 1$ in all four Quadrants.
(D) There is no value of $\theta$ on $0 \le \theta \le 2\pi$ for which $\tan \theta = 1$.

▶️ Answer/Explanation

Detailed solution

The correct option is (B).
The tangent function is defined as $\tan \theta = \frac{y}{x}$ in the Cartesian plane.
For $\tan \theta = 1$, the values of $x$ and $y$ must have the same sign and magnitude.
In Quadrant I, both $x > 0$ and $y > 0$, so $\tan \theta = \frac{+}{+} = 1$ at $\theta = \frac{\pi}{4}$.
In Quadrant III, both $x < 0$ and $y < 0$, so $\tan \theta = \frac{-}{-} = 1$ at $\theta = \frac{5\pi}{4}$.
In Quadrants II and IV, $x$ and $y$ have opposite signs, making $\tan \theta$ negative.
Thus, there are exactly two solutions in the interval $[0, 2\pi]$, located in Quadrants I and III.

Question

The function $j$ is given by $j(x) = 8 – 7\tan\left(\frac{x}{4}\right)$. Which of the following gives the vertical asymptotes of $j$?

(A) $x = \frac{\pi}{2} + \pi k$, where $k$ is an integer

(B) $x = \frac{\pi}{8} + \frac{\pi}{4}k$, where $k$ is an integer

(D) $x = 4\pi + 8\pi k$, where $k$ is an integer

▶️ Answer/Explanation

Detailed solution

The function is given by $j(x) = 8 – 7\tan\left(\frac{x}{4}\right)$.

Vertical asymptotes for the tangent function, $\tan(\theta)$, occur where the function is undefined, which is when the argument $\theta = \frac{\pi}{2} + \pi k$ for any integer $k$.

In this function, the argument of the tangent is $\frac{x}{4}$.

Set the argument equal to the condition for vertical asymptotes: $\frac{x}{4} = \frac{\pi}{2} + \pi k$.

Solve for $x$ by multiplying both sides of the equation by $4$.

$x = 4\left(\frac{\pi}{2}\right) + 4(\pi k)$.

Simplifying the expression results in: $x = 2\pi + 4\pi k$.

Therefore, the correct option is (C).

AP Precalculus -3.8 The Tangent Function- MCQ Exam Style Questions - Effective Fall 2023