AP Precalculus -3.9 Inverse Trigonometric Functions- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -3.9 Inverse Trigonometric Functions- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -3.9 Inverse Trigonometric Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The function $ f $ is given by $ f(x) = \frac{1}{2} \sin x $ for $ -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} $. What are the domain and range of the inverse function of $ f $?

(A) Domain: $[-\frac{1}{2}, \frac{1}{2}]$, Range: $[-\frac{\pi}{2}, \frac{\pi}{2}]$
(B) Domain: $[-1, 1]$, Range: $[-\frac{\pi}{2}, \frac{\pi}{2}]$
(C) Domain: $[-\frac{\pi}{2}, \frac{\pi}{2}]$, Range: $[-\frac{1}{2}, \frac{1}{2}]$
(D) Domain: $[-\frac{\pi}{2}, \frac{\pi}{2}]$, Range: $[-1, 1]$

▶️ Answer/Explanation

Detailed solution

For the original function $ f(x) = \frac{1}{2}\sin x $ on $ -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} $:
– Domain of $ f $: $ [-\frac{\pi}{2}, \frac{\pi}{2}] $
– Range of $ f $: Since $\sin x$ ranges from $-1$ to $1$ over this interval, $ \frac{1}{2}\sin x $ ranges from $-\frac{1}{2}$ to $\frac{1}{2}$.
For the inverse function $ f^{-1} $, the domain and range swap:
– Domain of $ f^{-1} $ = Range of $ f $ = $[-\frac{1}{2}, \frac{1}{2}]$
– Range of $ f^{-1} $ = Domain of $ f $ = $[-\frac{\pi}{2}, \frac{\pi}{2}]$
✅ Answer: (A)

Question

The graph of a sinusoidal function $ f $ is given. What is the length of the largest interval of input values of $ f $ on which an inverse function of $ f $ can be constructed?

(A) 1
(B) 2
(C) 4
(D) There is no interval larger than a single point on which $ f $ is invertible.

▶️ Answer/Explanation

Detailed solution

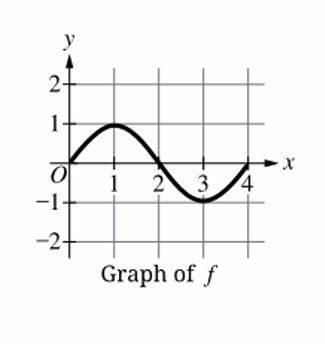
For a sinusoidal function to be invertible, it must be one-to-one on an interval. The longest such interval on a sine or cosine wave is half a period where the function is strictly increasing or decreasing.
From the graph (described in the PDF), the period is 4, so half-period is 2. This gives the longest interval for an inverse.
✅ Answer: (B)

Question

On a given day, the number of people, in thousands, that have entered a museum is modeled by the function $h$ given by $h(t)=4.217\tan^{-1}(0.7t-0.026)$, where $t$ is measured in hours and $0\le t\le8$ Based on the model, at what time $t$ did person number 4000 enter the museum?

(A) $t=1.121$
(B) $t=2.029$
(C) $t=5.165$
(D) $t=6.623$

▶️ Answer/Explanation

Detailed solution

1. Set up the equation:
Person number 4000 corresponds to 4 thousand people. So, set $h(t) = 4$.
$4 = 4.217\tan^{-1}(0.7t-0.026)$

2. Solve for $t$ using a calculator:
$\frac{4}{4.217} = \tan^{-1}(0.7t-0.026)$
$\tan(\frac{4}{4.217}) = 0.7t – 0.026$
$1.398 \approx 0.7t – 0.026$
$1.424 \approx 0.7t$
$t \approx 2.03$

✅ Answer: (B)

Question

Evaluate $\sec^{-1}(\csc(-\frac{\pi}{4}))$ for the exact value.

a. $\frac{\pi}{2}$

b. $\frac{3\pi}{4}$

c. $\pi$

d. $\frac{\pi}{4}$

▶️ Answer/Explanation

Detailed solution

The expression is $\sec^{-1}(\csc(-\frac{\pi}{4}))$.
First, evaluate the inner function: $\csc(-\frac{\pi}{4}) = \frac{1}{\sin(-\frac{\pi}{4})}$.
Since $\sin(-\frac{\pi}{4}) = -\frac{\sqrt{2}}{2}$, then $\csc(-\frac{\pi}{4}) = -\frac{2}{\sqrt{2}} = -\sqrt{2}$.
The expression simplifies to $\sec^{-1}(-\sqrt{2})$.
Recall the range of $y = \sec^{-1}(x)$ is $[0, \pi], y \neq \frac{\pi}{2}$.
We need an angle $\theta$ such that $\sec(\theta) = -\sqrt{2}$, which means $\cos(\theta) = -\frac{1}{\sqrt{2}}$.
In the second quadrant, the angle that satisfies this is $\theta = \frac{3\pi}{4}$.
Therefore, the exact value is $\frac{3\pi}{4}$, which corresponds to option b.

Question

Directions:

Unless otherwise specified, the domain of a function $ f $ is assumed to be the set of all real numbers $ x $ for which $ f(x) $ is a real number. Angle measures for trigonometric functions are assumed to be in radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be obtained without a calculator. For example, $ \log_2 8 $, $ \cos(\frac{\pi}{2}) $, and $ \sin^{-1}(1) $ can be evaluated without a calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and logarithms, where applicable. For example, $ 2x + 3x $, $ 5^2 \cdot 5^3 $, $ \frac{x^5}{x^2} $, and $ \ln 3 + \ln 5 $ should be rewritten in equivalent forms.
For each part of the question, show the work that leads to your answers.

Part A
The functions $ g $ and $ h $ are given by

$ g(x) = \log_5(4x – 2) $
$ h(x) = \sin^{-1}(8x) $

(i) Solve $ g(x) = 3 $ for values of $ x $ in the domain of $ g $.

(ii) Solve $ h(x) = \frac{\pi}{4} $ for values of $ x $ in the domain of $ h $.

Part B
The functions $ j $ and $ k $ are given by

$ j(x) = (\sec x)(\cot x) $
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $

(i) Rewrite $ j(x) $ as an expression involving $ \sin x $ and no other trigonometric functions.

(ii) Rewrite $ k(x) $ as an expression of the form $ 4^{(ax+b)} $, where $ a $ and $ b $ are constants.

Part C
The function $ m $ is given by

$ m(x) = \sqrt{3}\tan(x + \frac{\pi}{2}) $.

Find all values in the domain of $ m $ that yield an output value of 1.

▶️ Answer/Explanation

Detailed solution

Part A
(i) Solve $ g(x) = 3 $
Start with the given equation:
$ \log_5(4x – 2) = 3 $
Convert the logarithmic equation to exponential form ($ y = \log_b x \iff x = b^y $):
$ 4x – 2 = 5^3 $
Evaluate the exponent:
$ 4x – 2 = 125 $
Add 2 to both sides:
$ 4x = 127 $
Divide by 4:
$ x = \frac{127}{4} $

(ii) Solve $ h(x) = \frac{\pi}{4} $
Start with the given equation:
$ \sin^{-1}(8x) = \frac{\pi}{4} $
Take the sine of both sides to isolate the argument:
$ 8x = \sin\left(\frac{\pi}{4}\right) $
Substitute the exact value of $ \sin\left(\frac{\pi}{4}\right) $:
$ 8x = \frac{\sqrt{2}}{2} $
Divide by 8:
$ x = \frac{\sqrt{2}}{16} $

Part B
(i) Rewrite $ j(x) $
Start with the function definition:
$ j(x) = (\sec x)(\cot x) $
Substitute the reciprocal and quotient identities ($ \sec x = \frac{1}{\cos x} $ and $ \cot x = \frac{\cos x}{\sin x} $):
$ j(x) = \left(\frac{1}{\cos x}\right) \left(\frac{\cos x}{\sin x}\right) $
Cancel the $ \cos x $ terms:
$ j(x) = \frac{1}{\sin x} $

(ii) Rewrite $ k(x) $
Start with the function definition:
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $
To write in the form $ 4^{(ax+b)} $, convert bases 16 and 2 to base 4.
Since $ 16 = 4^2 $ and $ 2 = \sqrt{4} = 4^{1/2} = 4^{0.5} $:
$ k(x) = \frac{(4^2)^{3x} \cdot 4^x}{4^{0.5}} $
Apply the power of a power rule ($ (a^m)^n = a^{mn} $):
$ k(x) = \frac{4^{6x} \cdot 4^x}{4^{0.5}} $
Apply the product rule for exponents ($ a^m \cdot a^n = a^{m+n} $) in the numerator:
$ k(x) = \frac{4^{6x + x}}{4^{0.5}} = \frac{4^{7x}}{4^{0.5}} $
Apply the quotient rule for exponents ($ \frac{a^m}{a^n} = a^{m-n} $):
$ k(x) = 4^{7x – 0.5} $ (or $ 4^{7x – \frac{1}{2}} $)
Thus, $ a = 7 $ and $ b = -0.5 $.

Part C
Find values where $ m(x) = 1 $
Set the function equal to 1:
$ \sqrt{3}\tan\left(x + \frac{\pi}{2}\right) = 1 $
Isolate the tangent function by dividing by $ \sqrt{3} $:
$ \tan\left(x + \frac{\pi}{2}\right) = \frac{1}{\sqrt{3}} $
Determine the reference angle. We know that $ \tan\left(\frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} $.
Set up the general solution for tangent ($ \theta = \text{ref} + n\pi $):
$ x + \frac{\pi}{2} = \frac{\pi}{6} + n\pi $, where $ n $ is any integer.
Solve for $ x $ by subtracting $ \frac{\pi}{2} $ from both sides:
$ x = \frac{\pi}{6} – \frac{\pi}{2} + n\pi $
Find a common denominator (6) to combine fractions:
$ x = \frac{\pi}{6} – \frac{3\pi}{6} + n\pi $
$ x = -\frac{2\pi}{6} + n\pi $
Simplify the fraction:
$ x = -\frac{\pi}{3} + n\pi $

AP Precalculus -3.9 Inverse Trigonometric Functions- MCQ Exam Style Questions - Effective Fall 2023