AP Precalculus -3.9 Inverse Trigonometric Functions- Study Notes - Effective Fall 2023
AP Precalculus -3.9 Inverse Trigonometric Functions- Study Notes – Effective Fall 2023
AP Precalculus -3.9 Inverse Trigonometric Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Construct analytical and graphical representations of the inverse of the sine, cosine, and tangent functions over a restricted domain.
Key Concepts:
Inverse Trigonometric Functions
Arcsine, Arccosine, and Arctangent
Restricted Domains for Inverse Trigonometric Functions
Inverse Trigonometric Functions
An inverse trigonometric function reverses the input–output relationship of its corresponding trigonometric function.
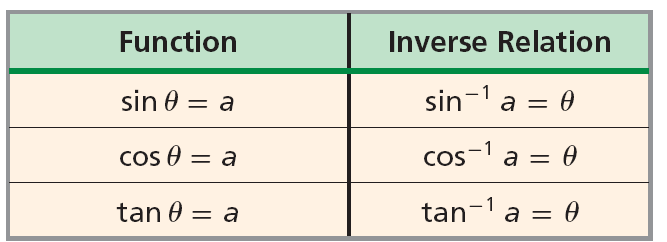
This means the input and output values are switched compared to the original trigonometric function.
As a result:
The input of an inverse trigonometric function is a value from the range of the original trigonometric function.
The output is an angle measure.
For example:
If \( y = \sin \theta \), then \( \theta = \sin^{-1}(y) \).
Inverse trigonometric functions are written using the notation:
\( \sin^{-1} x \), \( \cos^{-1} x \), \( \tan^{-1} x \)
These expressions do not represent reciprocals. Instead, they represent functions that return an angle whose trigonometric value is the given input.
Because trigonometric functions are not one-to-one over their entire domains, inverse trigonometric functions are defined using restricted domains so that each input corresponds to exactly one output angle.
Example:
Evaluate \( \sin^{-1}\!\left(\dfrac{1}{2}\right) \).
▶️ Answer/Explanation
The expression asks for the angle whose sine is \( \dfrac{1}{2} \).
From the unit circle,
\( \sin\!\left(\dfrac{\pi}{6}\right) = \dfrac{1}{2} \)
Since \( \dfrac{\pi}{6} \) lies in the principal range of \( \sin^{-1} \),
\( \sin^{-1}\!\left(\dfrac{1}{2}\right) = \dfrac{\pi}{6} \)
Example:
Interpret the meaning of \( \tan^{-1}(1) \).
▶️ Answer/Explanation
This expression asks for the angle whose tangent is 1.
From known values,
\( \tan\!\left(\dfrac{\pi}{4}\right) = 1 \)
Since \( \dfrac{\pi}{4} \) lies in the principal range of \( \tan^{-1} \),
\( \tan^{-1}(1) = \dfrac{\pi}{4} \)
Conclusion: The output of an inverse trigonometric function is an angle measure.
Arcsine, Arccosine, and Arctangent
The inverse trigonometric functions are called: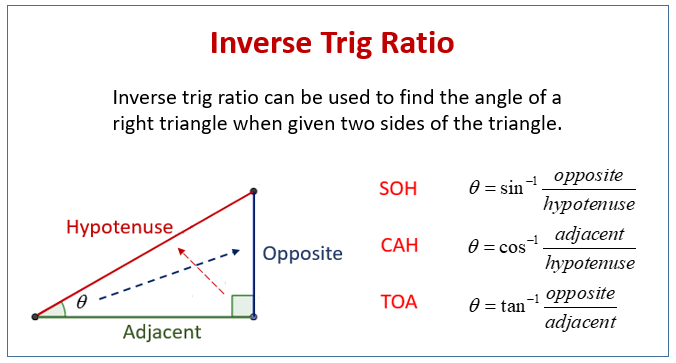
arcsine, written as \( \sin^{-1}x \)
arccosine, written as \( \cos^{-1}x \)
arctangent, written as \( \tan^{-1}x \)
These functions are also commonly written as
\( \arcsin x \), \( \arccos x \), and \( \arctan x \).
Because the sine, cosine, and tangent functions are periodic, they are not one-to-one over their entire domains.
To define inverse functions, their domains must be restricted so that each output value corresponds to exactly one input value.
Restricted Domains
The standard restricted domains used to define the inverse trigonometric functions are:
For \( \sin \theta \): \( \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \)
For \( \cos \theta \): \( [0, \pi] \)
For \( \tan \theta \): \( \left( -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right) \)
These restrictions ensure that the inverse trigonometric functions return a unique angle measure.
Example:
Explain why the sine function must have a restricted domain in order for \( \sin^{-1}x \) to be a function.
▶️ Answer/Explanation
The sine function is periodic and repeats its values infinitely many times.
Without restricting its domain, a single output value would correspond to multiple angle measures.
Restricting the domain to \( \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \) ensures each sine value comes from exactly one angle.
Example:
Evaluate \( \cos^{-1}(-1) \).
▶️ Answer/Explanation
This asks for the angle in \( [0, \pi] \) whose cosine is −1.
From the unit circle,
\( \cos(\pi) = -1 \)
Therefore,
\( \cos^{-1}(-1) = \pi \)
Restricted Domains for Inverse Trigonometric Functions
To define inverse trigonometric functions, the corresponding trigonometric functions must be restricted to specific domains so that they are one-to-one.
These restricted domains ensure that each input value corresponds to exactly one output angle.
Standard Restricted Domains
Sine function: \( \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] \)
Cosine function: \( [0, \pi] \)
Tangent function: \( \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \)
As a result:
\( \sin^{-1}x \) returns angles in \( \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] \)
\( \cos^{-1}x \) returns angles in \( [0, \pi] \)
\( \tan^{-1}x \) returns angles in \( \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \)
These intervals are called the principal ranges of the inverse trigonometric functions.
| Function | Domain | Range | Graph |
| \( \arcsin x \) | \( -1 \le x \le 1 \) | \( -\dfrac{\pi}{2} \le y \le \dfrac{\pi}{2} \) | 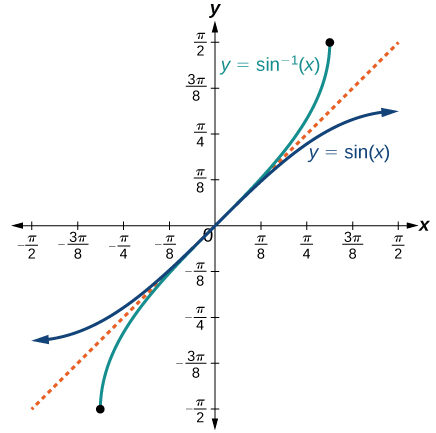 |
| \( \arccos x \) | \( -1 \le x \le 1 \) | \( 0 \le y \le \pi \) | 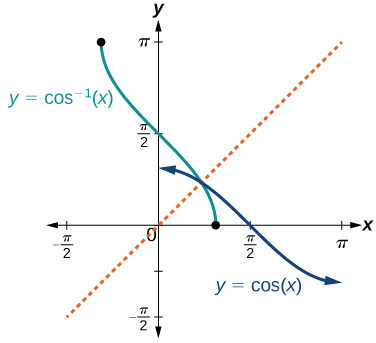 |
| \( \arctan x \) | \( x \in \mathbb{R} \) | \( -\dfrac{\pi}{2} < y < \dfrac{\pi}{2} \) | 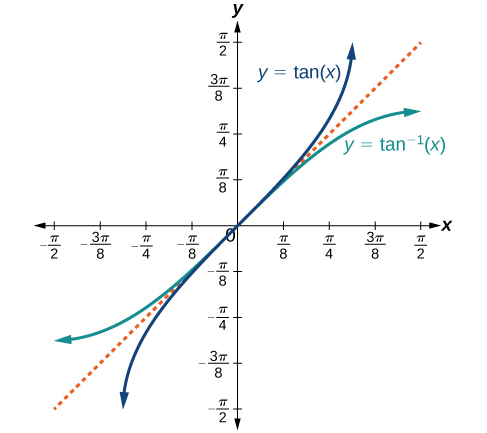 |
Example:
Evaluate \( \sin^{-1}(\sin \dfrac{5\pi}{6}) \).
▶️ Answer/Explanation
First, find the sine value:
\( \sin\!\left(\dfrac{5\pi}{6}\right) = \dfrac{1}{2} \)
Now find the angle in the restricted domain \( \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] \) whose sine is \( \dfrac{1}{2} \).
\( \sin^{-1}\!\left(\dfrac{1}{2}\right) = \dfrac{\pi}{6} \)
Final answer: \( \dfrac{\pi}{6} \)
Example:
Evaluate \( \cos^{-1}(\cos \dfrac{7\pi}{6}) \).
▶️ Answer/Explanation
First, compute the cosine value:
\( \cos\!\left(\dfrac{7\pi}{6}\right) = -\dfrac{\sqrt{3}}{2} \)
Now find the angle in the restricted domain \( [0, \pi] \) with this cosine value.
\( \cos^{-1}\!\left(-\dfrac{\sqrt{3}}{2}\right) = \dfrac{5\pi}{6} \)
Final answer: \( \dfrac{5\pi}{6} \)
