AP Precalculus -4.12 Linear Transformations and Matrices- Study Notes - Effective Fall 2023
AP Precalculus -4.12 Linear Transformations and Matrices- Study Notes – Effective Fall 2023
AP Precalculus -4.12 Linear Transformations and Matrices- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine the output vectors of a linear transformation using a 2× 2 matrix.
Key Concepts:
Linear Transformations
Effect of Linear Transformations on the Zero Vector
Vectors in R2 as Matrices
Matrix Representation of Linear Transformations in R2
Applying a Linear Transformation to Multiple Vectors
Linear Transformations
A linear transformation is a function that maps an input vector to an output vector.
Each component of the output vector is formed as the sum of constant multiples of the components of the input vector.
![]()
In two dimensions, a linear transformation can be written in matrix form as
\( \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \)
This means
\( x’ = ax + by \)
\( y’ = cx + dy \)
Linear transformations are used to describe geometric operations such as rotations, reflections, stretches, and shears.
Example:
Let the linear transformation be defined by
\( T(\mathbf{v}) = \begin{pmatrix} 2 & 1 \\ -1 & 3 \end{pmatrix} \mathbf{v} \)
Find the image of the vector \( \mathbf{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \).
▶️ Answer/Explanation
Multiply the matrix by the vector:
\( T(\mathbf{v}) = \begin{pmatrix} 2(1) + 1(2) \\ -1(1) + 3(2) \end{pmatrix} = \begin{pmatrix} 4 \\ 5 \end{pmatrix} \)
Conclusion: The output vector is \( \begin{pmatrix} 4 \\ 5 \end{pmatrix} \).
Example:
Describe the transformation represented by the matrix
\( \begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix} \)
▶️ Answer/Explanation
The output vector satisfies
\( x’ = 3x \), \( y’ = y \)
This stretches vectors horizontally by a factor of 3 while leaving vertical components unchanged.
Conclusion: The transformation is a horizontal stretch.
Effect of Linear Transformations on the Zero Vector
A fundamental property of a linear transformation is that it maps the zero vector to the zero vector.
\( T(\mathbf{0}) = \mathbf{0} \)
This property follows directly from the definition of a linear transformation, since each component of the output vector is a sum of constant multiples of the input vector components.
When all input components are zero, every constant multiple is zero, so the output vector must also be the zero vector.
Geometrically, this means that all linear transformations leave the origin fixed.
Example:
Let the linear transformation be defined by
\( T(\mathbf{v}) = \begin{pmatrix} 2 & -1 \\ 4 & 3 \end{pmatrix} \mathbf{v} \)
Find \( T(\mathbf{0}) \).
▶️ Answer/Explanation
The zero vector is
\( \mathbf{0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \)
Multiply:
\( T(\mathbf{0}) = \begin{pmatrix} 2 & -1 \\ 4 & 3 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \)
Conclusion: The zero vector maps to the zero vector.
Example:
Explain why a function that does not map the zero vector to the zero vector cannot be a linear transformation.
▶️ Answer/Explanation
If a function sends the zero vector to a nonzero vector, then it cannot be expressed as sums of constant multiples of input components.
Therefore, it violates the defining property of linear transformations.
Conclusion: Mapping the zero vector to itself is required for linearity.
Vectors in \( \mathbb{R}^2 \) as Matrices
Vectors in \( \mathbb{R}^2 \) can be represented conveniently using matrices.
Single Vector Representation
A single vector in \( \mathbb{R}^2 \) can be written as a \( 2 \times 1 \) matrix, also called a column vector.
\( \mathbf{v} = \begin{pmatrix} x \\ y \end{pmatrix} \)
Here, the two entries represent the x- and y-components of the vector.
Multiple Vector Representation
A set of \( n \) vectors in \( \mathbb{R}^2 \) can be arranged as columns of a \( 2 \times n \) matrix.
\( \begin{pmatrix} x_1 & x_2 & \dots & x_n \\ y_1 & y_2 & \dots & y_n \end{pmatrix} \)
Each column corresponds to one vector in \( \mathbb{R}^2 \).
This representation is especially useful when applying linear transformations to multiple vectors at once.
Example:
Write the vector \( \langle 3, -1 \rangle \) as a matrix.
▶️ Answer/Explanation
\( \begin{pmatrix} 3 \\ -1 \end{pmatrix} \)
Conclusion: The vector is a \( 2 \times 1 \) matrix.
Example:
Represent the vectors \( \langle 1, 2 \rangle \), \( \langle -1, 0 \rangle \), and \( \langle 3, 4 \rangle \) as a matrix.
▶️ Answer/Explanation
Place each vector as a column:
\( \begin{pmatrix} 1 & -1 & 3 \\ 2 & 0 & 4 \end{pmatrix} \)
Conclusion: The result is a \( 2 \times 3 \) matrix.
Matrix Representation of Linear Transformations in \( \mathbb{R}^2 \)
For a linear transformation \( L \) from \( \mathbb{R}^2 \) to \( \mathbb{R}^2 \), there exists a unique \( 2 \times 2 \) matrix \( A \) such that
\( L(\mathbf{v}) = A\mathbf{v} \)
for every vector \( \mathbf{v} \in \mathbb{R}^2 \).
This means that every linear transformation in \( \mathbb{R}^2 \) can be represented exactly by matrix multiplication.
Conversely, if \( A \) is any \( 2 \times 2 \) matrix, then the function defined by
\( L(\mathbf{v}) = A\mathbf{v} \)
is a linear transformation from \( \mathbb{R}^2 \) to \( \mathbb{R}^2 \).
This establishes a one-to-one correspondence between linear transformations in \( \mathbb{R}^2 \) and \( 2 \times 2 \) matrices.
Example:
Let the linear transformation \( L \) satisfy
\( L\!\left(\begin{pmatrix}1\\0\end{pmatrix}\right)= \begin{pmatrix}2\\1\end{pmatrix}, \quad L\!\left(\begin{pmatrix}0\\1\end{pmatrix}\right)= \begin{pmatrix}-1\\3\end{pmatrix} \)
Find the matrix \( A \) such that \( L(\mathbf{v}) = A\mathbf{v} \).
▶️ Answer/Explanation
The columns of \( A \) are the images of the standard basis vectors.
\( A = \begin{pmatrix} 2 & -1 \\ 1 & 3 \end{pmatrix} \)
Conclusion: This matrix uniquely represents the linear transformation \( L \).
Example:
Let
\( A = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \)
Define \( L(\mathbf{v}) = A\mathbf{v} \). Describe the transformation.
▶️ Answer/Explanation
For \( \mathbf{v} = \begin{pmatrix}x\\y\end{pmatrix} \),
\( L(\mathbf{v}) = \begin{pmatrix}-y\\x\end{pmatrix} \)
This corresponds to a rotation of vectors by \( \dfrac{\pi}{2} \) radians counterclockwise about the origin.
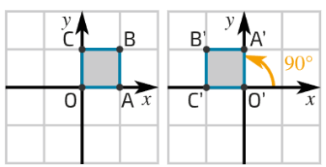
Conclusion: Any \( 2 \times 2 \) matrix defines a linear transformation in \( \mathbb{R}^2 \).
Applying a Linear Transformation to Multiple Vectors
Let \( A \) be a \( 2 \times 2 \) matrix that represents a linear transformation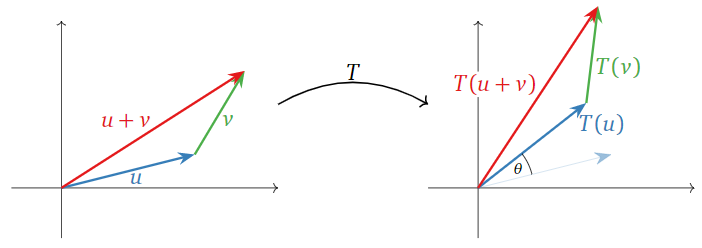
\( L(\mathbf{v}) = A\mathbf{v} \)
in \( \mathbb{R}^2 \).
If we have n input vectors in \( \mathbb{R}^2 \), they can be arranged as columns of a \( 2 \times n \) matrix
\( V = \begin{pmatrix} \mathbf{v}_1 & \mathbf{v}_2 & \dots & \mathbf{v}_n \end{pmatrix} \)
Multiplying the transformation matrix \( A \) by this matrix of input vectors produces a \( 2 \times n \) matrix of output vectors:
\( AV = \begin{pmatrix} A\mathbf{v}_1 & A\mathbf{v}_2 & \dots & A\mathbf{v}_n \end{pmatrix} \)
Each column of the resulting matrix is the image of the corresponding input vector under the linear transformation.
This method allows multiple vectors to be transformed simultaneously using a single matrix multiplication.
Example:
Let
\( A = \begin{pmatrix} 2 & 0 \\ 1 & 1 \end{pmatrix} \)
and let the input vectors be
\( V = \begin{pmatrix} 1 & 0 & -1 \\ 2 & 1 & 3 \end{pmatrix} \)
Find the matrix of output vectors.
▶️ Answer/Explanation
Multiply \( A \) by \( V \):
\( AV = \begin{pmatrix} 2 & 0 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -1 \\ 2 & 1 & 3 \end{pmatrix} = \begin{pmatrix} 2 & 0 & -2 \\ 3 & 1 & 2 \end{pmatrix} \)
Conclusion: Each column represents the transformed version of the corresponding input vector.
Example:
Explain why the product \( AV \) applies the transformation to each vector individually.
▶️ Answer/Explanation
Matrix multiplication operates column by column.
Each column of \( V \) is multiplied by \( A \), producing \( A\mathbf{v}_1, A\mathbf{v}_2, \dots, A\mathbf{v}_n \).
Conclusion: A single matrix multiplication applies the linear transformation to all input vectors at once.
