AP Precalculus -4.2 Parametric Modeling of Planar Motion- Study Notes - Effective Fall 2023
AP Precalculus -4.2 Parametric Modeling of Planar Motion- Study Notes – Effective Fall 2023
AP Precalculus -4.2 Parametric Modeling of Planar Motion- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify key characteristics of a parametric planar motion function that are related to position.
Key Concepts:
Parametric Functions and Particle Motion
Horizontal and Vertical Extrema in Particle Motion
Intercepts of Parametric Curves
Parametric Functions and Particle Motion
A parametric function of the form
\( \mathbf{f}(t) = (x(t), y(t)) \)

can be used to model the motion of a particle in the plane.
In this interpretation, the parameter \( t \) represents time, and the ordered pair \( (x(t), y(t)) \) represents the position of the particle at time \( t \).
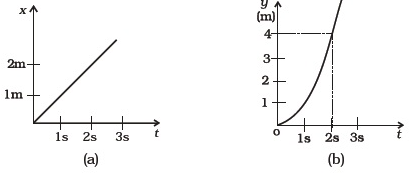
As time increases, the graph of the parametric function traces the path of the particle, while the order of the points indicates the direction of motion.
The starting position of the particle corresponds to the smallest value of \( t \) in the domain, and the ending position corresponds to the largest value of \( t \).
Parametric models are especially useful for describing motion where both horizontal and vertical positions change with time.
Example:
A particle moves according to
\( x(t) = 2t, \quad y(t) = t + 1 \)
Find the position of the particle at time \( t = 3 \).
▶️ Answer/Explanation
Evaluate the parametric function at \( t = 3 \):
\( x(3) = 2(3) = 6 \)
\( y(3) = 3 + 1 = 4 \)
Final answer: The particle is at position \( (6, 4) \) at time \( t = 3 \).
Example:
A particle moves according to the parametric function
\( \mathbf{f}(t) = (\cos t, \sin t) \), \( 0 \le t \le 2\pi \)
Describe the motion of the particle.
▶️ Answer/Explanation
For all values of \( t \), the position satisfies
\( x^2 + y^2 = \cos^2 t + \sin^2 t = 1 \)
This represents a circle of radius 1 centered at the origin.
As \( t \) increases, the particle moves counterclockwise around the circle, starting and ending at \( (1,0) \).
Conclusion: The parametric function models uniform circular motion in the plane.
Horizontal and Vertical Extrema in Particle Motion
When a particle’s motion in the plane is modeled by a parametric function
\( \mathbf{f}(t) = (x(t), y(t)) \)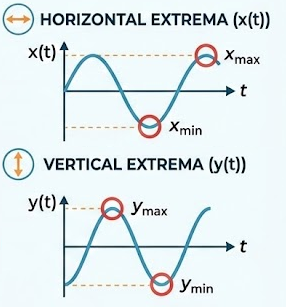
the horizontal extrema of the motion correspond to the maximum and minimum values of \( x(t) \), and the vertical extrema correspond to the maximum and minimum values of \( y(t) \).
These extrema describe the furthest left, furthest right, highest, and lowest positions reached by the particle during its motion.
Identifying extrema is useful for understanding the bounds of motion and the overall shape of the path traced by the particle.
Extrema can be found by analyzing the functions \( x(t) \) and \( y(t) \) over the given domain of \( t \).
Example:
A particle moves according to
\( x(t) = 3\cos t, \quad y(t) = 2\sin t \), \( 0 \le t \le 2\pi \)
Find the horizontal and vertical extrema.
▶️ Answer/Explanation
Horizontal extrema
Since \( -1 \le \cos t \le 1 \),
\( -3 \le x(t) \le 3 \)
The particle reaches \( x = 3 \) and \( x = -3 \).
Vertical extrema
Since \( -1 \le \sin t \le 1 \),
\( -2 \le y(t) \le 2 \)
The particle reaches \( y = 2 \) and \( y = -2 \).
Conclusion: The motion is bounded within the rectangle \( -3 \le x \le 3 \), \( -2 \le y \le 2 \).
Example:
A particle moves according to
\( x(t) = t^2 – 4t, \quad y(t) = 5 – t \), \( 0 \le t \le 4 \)
Find the horizontal and vertical extrema.
▶️ Answer/Explanation
Horizontal extrema
Evaluate \( x(t) \) at the endpoints and the vertex:
\( x(0) = 0,\quad x(2) = -4,\quad x(4) = 0 \)
Minimum value: \( x = -4 \)
Vertical extrema
Since \( y(t) = 5 – t \) is decreasing on the interval,
\( y(0) = 5,\quad y(4) = 1 \)
Conclusion: The particle reaches a leftmost position at \( x = -4 \), a highest position at \( y = 5 \), and a lowest position at \( y = 1 \).
Intercepts of Parametric Curves
For a parametric function written as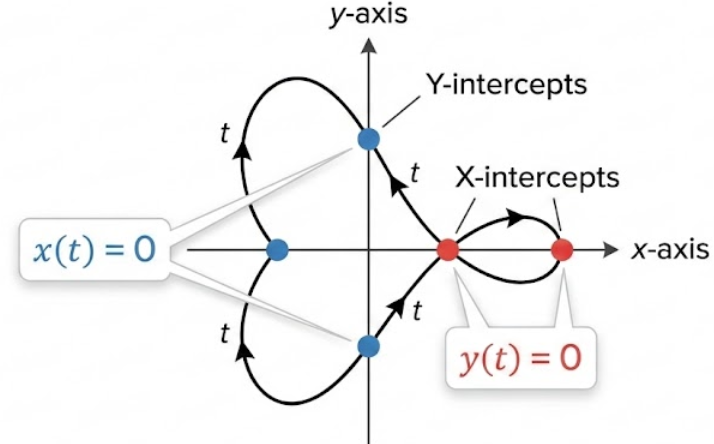
\( \mathbf{f}(t) = (x(t), y(t)) \)
intercepts of the graph can be identified by analyzing the zeros of the component functions.
Y-intercepts occur when the graph crosses the \( y \)-axis, which happens when \( x = 0 \).
Therefore, the real zeros of \( x(t) \) correspond to y-intercepts.
X-intercepts occur when the graph crosses the \( x \)-axis, which happens when \( y = 0 \).
Therefore, the real zeros of \( y(t) \) correspond to x-intercepts.
Because parametric curves may pass through the same intercept at multiple parameter values, each real zero of \( x(t) \) or \( y(t) \) must be checked within the given domain of \( t \).
Example:
Consider the parametric equations
\( x(t) = t – 2, \quad y(t) = t^2 – 4 \)
Find the \( x \)- and \( y \)-intercepts.
▶️ Answer/Explanation
Y-intercept
Set \( x(t) = 0 \):
\( t – 2 = 0 \Rightarrow t = 2 \)
Evaluate \( y(2) \):
\( y(2) = 2^2 – 4 = 0 \)
So the y-intercept is \( (0, 0) \).
X-intercepts
Set \( y(t) = 0 \):
\( t^2 – 4 = 0 \Rightarrow t = \pm 2 \)
Evaluate \( x(t) \):
\( x(2) = 0,\quad x(-2) = -4 \)
Conclusion: The x-intercepts are \( (0,0) \) and \( (-4,0) \).
Example:
A particle moves according to
\( x(t) = \cos t, \quad y(t) = \sin t \), \( 0 \le t \le 2\pi \)
Identify the intercepts.
▶️ Answer/Explanation
Y-intercepts
Set \( x(t) = 0 \):
\( \cos t = 0 \Rightarrow t = \dfrac{\pi}{2}, \dfrac{3\pi}{2} \)
Corresponding points:
\( (0,1) \) and \( (0,-1) \)
X-intercepts
Set \( y(t) = 0 \):
\( \sin t = 0 \Rightarrow t = 0, \pi, 2\pi \)
Corresponding points:
\( (1,0), (-1,0), (1,0) \)
Conclusion: The curve intersects both axes multiple times due to its circular path.
