AP Precalculus -4.3 Parametric Rates of Change- Study Notes - Effective Fall 2023
AP Precalculus -4.3 Parametric Rates of Change- Study Notes – Effective Fall 2023
AP Precalculus -4.3 Parametric Rates of Change- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify key characteristics of a parametric planar motion function that are related to direction and rate of change.
Key Concepts:
Direction of Motion in Parametric Particle Motion
Dependence of Direction of Motion on the Parameter
Different Parametrizations of the Same Curve
Average Rate of Change and Secant Slope for Parametric Curves
Direction of Motion in Parametric Particle Motion
When a particle’s motion in the plane is modeled by a parametric function
\( \mathbf{f}(t) = (x(t), y(t)) \)
the direction of motion as the parameter \( t \) increases can be analyzed by considering the functions \( x(t) \) and \( y(t) \) independently.
Horizontal motion depends on how \( x(t) \) changes:
• If \( x(t) \) is increasing, the particle moves to the right.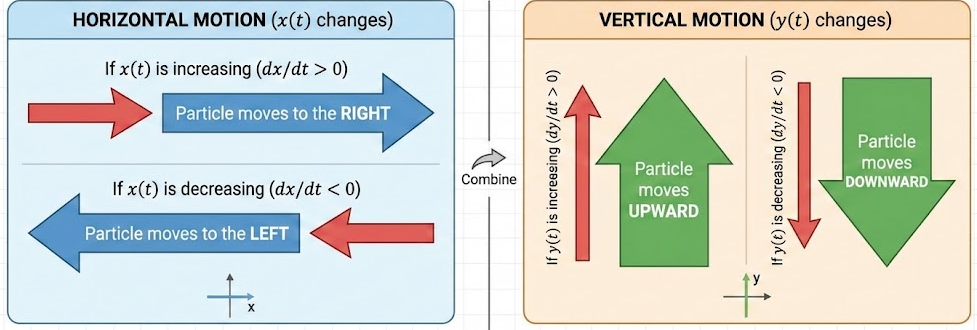
• If \( x(t) \) is decreasing, the particle moves to the left.
Vertical motion depends on how \( y(t) \) changes:
• If \( y(t) \) is increasing, the particle moves upward.
• If \( y(t) \) is decreasing, the particle moves downward.
By combining the horizontal and vertical directions, the overall direction of motion at any time can be determined.
Example:
A particle moves according to
\( x(t) = t^2 – 4t, \quad y(t) = 3t \), \( 0 \le t \le 5 \)
Describe the direction of motion for \( 0 < t < 2 \) and for \( t > 2 \).
▶️ Answer/Explanation
Horizontal motion
\( x(t) = t^2 – 4t \) decreases for \( 0 < t < 2 \) and increases for \( t > 2 \).
So the particle moves left for \( 0 < t < 2 \), then right for \( t > 2 \).
Vertical motion
\( y(t) = 3t \) is increasing for all \( t \ge 0 \).
So the particle always moves upward.
Conclusion: The particle moves up and left for \( 0 < t < 2 \), then up and right for \( t > 2 \).
Example:
A particle moves according to
\( x(t) = \cos t, \quad y(t) = \sin t \), \( 0 \le t \le 2\pi \)
Describe the direction of motion at \( t = \dfrac{\pi}{2} \).
▶️ Answer/Explanation
Near \( t = \dfrac{\pi}{2} \), \( x(t) = \cos t \) is decreasing, so the motion is to the left.
Near \( t = \dfrac{\pi}{2} \), \( y(t) = \sin t \) is decreasing, so the motion is downward.
Conclusion: At \( t = \dfrac{\pi}{2} \), the particle is moving down and to the left.
Dependence of Direction of Motion on the Parameter
For a particle whose motion in the plane is modeled by a parametric function
\( \mathbf{f}(t) = (x(t), y(t)) \)
the direction of planar motion at a point depends on how the functions \( x(t) \) and \( y(t) \) are changing at that specific value of the parameter \( t \).
It is possible for a particle to pass through the same point in the plane at different values of \( t \), while moving in different directions each time.
This occurs because direction is determined by whether \( x(t) \) and \( y(t) \) are increasing or decreasing at that moment, not just by the location of the point.
Therefore, a single point on a parametric curve does not uniquely determine the direction of motion unless the corresponding value of \( t \) is known.
Example:
Consider the parametric equations
\( x(t) = t^2 – 1, \quad y(t) = t^3 – t \)
The particle passes through the point \( (0,0) \) at more than one value of \( t \).
▶️ Answer/Explanation
Find values of \( t \) for which the particle is at \( (0,0) \):
\( x(t) = 0 \Rightarrow t^2 – 1 = 0 \Rightarrow t = \pm 1 \)
\( y(1) = 1^3 – 1 = 0, \quad y(-1) = (-1)^3 – (-1) = 0 \)
At \( t = 1 \), near this point, both \( x(t) \) and \( y(t) \) are increasing, so the motion is to the right and upward.
At \( t = -1 \), near this point, \( x(t) \) is decreasing while \( y(t) \) is increasing, so the motion is to the left and upward.
Conclusion: The particle passes through the same point \( (0,0) \) but with different directions of motion at different values of \( t \).
Example:
Explain why knowing only the graph of a parametric curve is not always enough to determine direction of motion.
▶️ Answer/Explanation
A graph shows the set of points traced by the particle but does not indicate how the parameter \( t \) changes.
Without information about increasing or decreasing values of \( t \), the direction of motion at a point cannot be uniquely determined.
Conclusion: Direction of motion depends on both position and the parameter value.
Different Parametrizations of the Same Curve
A single curve in the plane can often be represented by different parametric functions.
Although these parametric functions may use different formulas or different parameters, they can trace the same set of points in the plane.
Changing the parametric equations can also change the direction in which the curve is traversed and the speed at which the curve is traced.
Therefore, the same curve can be traversed forward or backward, faster or slower, depending on how it is parametrized.
This highlights the distinction between the geometric path of a curve and the parametric description used to generate it.
Example:
Consider the unit circle.
One parametrization is
\( \mathbf{f}_1(t) = (\cos t, \sin t) \), \( 0 \le t \le 2\pi \)
Another parametrization is
\( \mathbf{f}_2(t) = (\cos(2t), \sin(2t)) \), \( 0 \le t \le \pi \)
▶️ Answer/Explanation
Both parametrizations satisfy
\( x^2 + y^2 = 1 \)
so they trace the same circle.
However, \( \mathbf{f}_2(t) \) traces the circle twice as fast as \( \mathbf{f}_1(t) \).
Conclusion: Different parametrizations can trace the same curve at different speeds.
Example:
The parabola \( y = x^2 \) can be parametrized in different ways.
Two possible parametrizations are
\( \mathbf{f}_1(t) = (t, t^2) \)
\( \mathbf{f}_2(t) = (-t, t^2) \)
▶️ Answer/Explanation
Both parametrizations satisfy \( y = x^2 \), so they describe the same curve.
However, \( \mathbf{f}_1(t) \) traces the parabola from left to right, while \( \mathbf{f}_2(t) \) traces it from right to left.
Conclusion: The same curve can be traversed in different directions using different parametric functions.
Average Rate of Change and Secant Slope for Parametric Curves
For a parametric function
\( \mathbf{f}(t) = (x(t), y(t)) \)
the average rate of change of each component can be computed independently over an interval \( [t_1, t_2] \).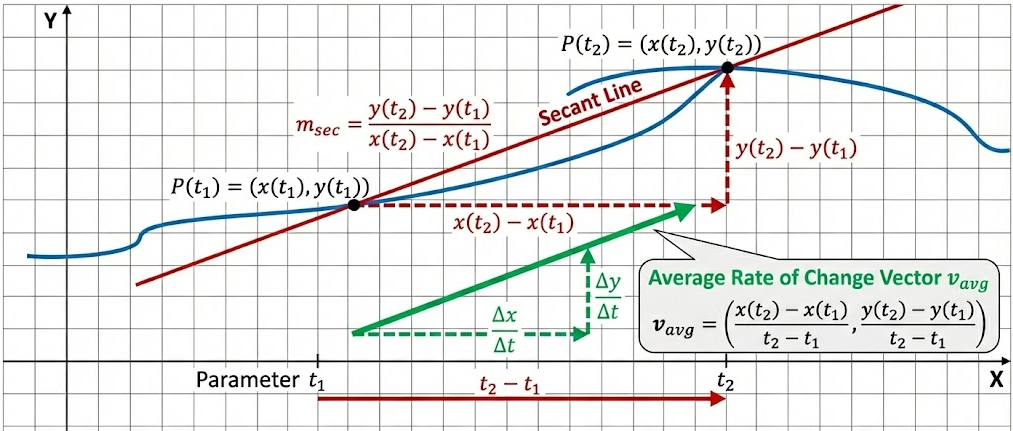
The average rate of change of \( x(t) \) is
\( \dfrac{x(t_2) – x(t_1)}{t_2 – t_1} \)
and the average rate of change of \( y(t) \) is
\( \dfrac{y(t_2) – y(t_1)}{t_2 – t_1} \)
If the average rate of change of \( x(t) \) is not zero, then the slope of the secant line between the two points on the curve corresponding to \( t_1 \) and \( t_2 \) is given by
\( \text{slope} = \dfrac{\text{average rate of change of } y}{\text{average rate of change of } x} = \dfrac{y(t_2) – y(t_1)}{x(t_2) – x(t_1)} \)
This slope represents the slope of the line segment connecting the two points on the parametric curve.
Example:
Given the parametric equations
\( x(t) = t^2, \quad y(t) = t^3 \)
find the slope of the secant line between \( t_1 = 1 \) and \( t_2 = 2 \).
▶️ Answer/Explanation
Compute the coordinates:
\( x(1) = 1,\; y(1) = 1 \)
\( x(2) = 4,\; y(2) = 8 \)
Compute the slope:
\( \dfrac{8 – 1}{4 – 1} = \dfrac{7}{3} \)
Conclusion: The slope of the secant line is \( \dfrac{7}{3} \).
Example:
A particle moves according to
\( x(t) = 3t – 1, \quad y(t) = 2t^2 \)
Find the slope of the secant line between \( t_1 = 0 \) and \( t_2 = 2 \).
▶️ Answer/Explanation
Evaluate the points:
\( x(0) = -1,\; y(0) = 0 \)
\( x(2) = 5,\; y(2) = 8 \)
Compute the slope:
\( \dfrac{8 – 0}{5 – (-1)} = \dfrac{8}{6} = \dfrac{4}{3} \)
Conclusion: The slope of the secant line between the two points is \( \dfrac{4}{3} \).
