AP Precalculus -4.4 Parametrically Defined Circles and Lines- Study Notes - Effective Fall 2023
AP Precalculus -4.4 Parametrically Defined Circles and Lines- Study Notes – Effective Fall 2023
AP Precalculus -4.4 Parametrically Defined Circles and Lines- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Express motion around a circle or along a line segment parametrically.
Key Concepts:
Parametric Model of a Complete Revolution on the Unit Circle
Transformations of the Unit Circle Parametric Function
Parametrizing a Linear Path Between Two Points
Parametric Model of a Complete Revolution on the Unit Circle
A complete counterclockwise revolution around the unit circle, centered at the origin and starting at the point \( (1, 0) \), can be modeled using parametric equations.
The parametric function is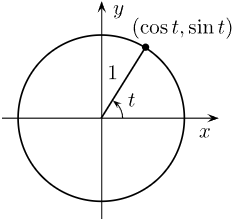
\( (x(t), y(t)) = (\cos t, \sin t) \)
with domain
\( 0 \le t \le 2\pi \)
At any value of \( t \), the point \( (\cos t, \sin t) \) lies on the unit circle because
\( \cos^2 t + \sin^2 t = 1 \)
As \( t \) increases from \( 0 \) to \( 2\pi \), the point moves counterclockwise exactly once around the circle, returning to the starting point \( (1,0) \).
Example:
Find the position of the particle at key values of \( t \) for the parametric function
\( (x(t), y(t)) = (\cos t, \sin t) \)
▶️ Answer/Explanation
| \( t \) | \( x(t) \) | \( y(t) \) |
|---|---|---|
| 0 | 1 | 0 |
| \( \dfrac{\pi}{2} \) | 0 | 1 |
| \( \pi \) | -1 | 0 |
| \( \dfrac{3\pi}{2} \) | 0 | -1 |
| \( 2\pi \) | 1 | 0 |
Conclusion: These points confirm one full counterclockwise revolution around the unit circle.
Example:
Describe the direction of motion for the parametric function
\( (x(t), y(t)) = (\cos t, \sin t) \), \( 0 \le t \le 2\pi \)
▶️ Answer/Explanation
As \( t \) increases:
• \( x(t) = \cos t \) initially decreases, so the motion starts to the left.
• \( y(t) = \sin t \) initially increases, so the motion starts upward.
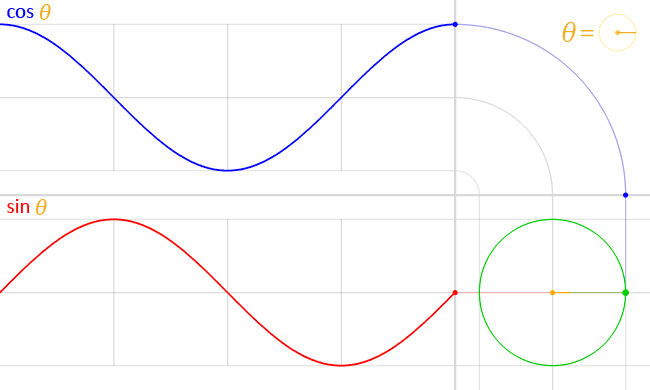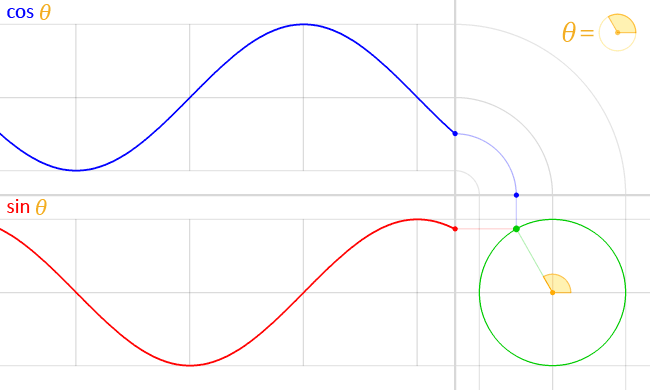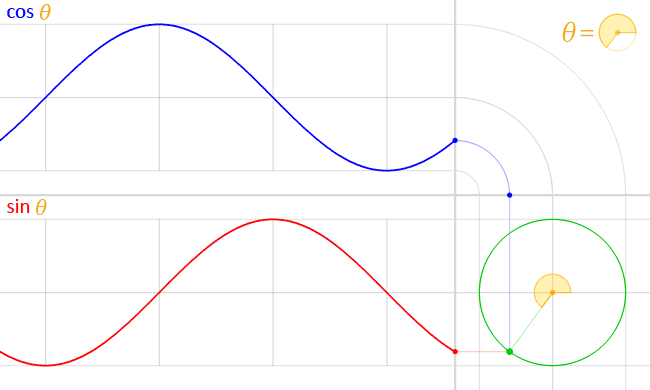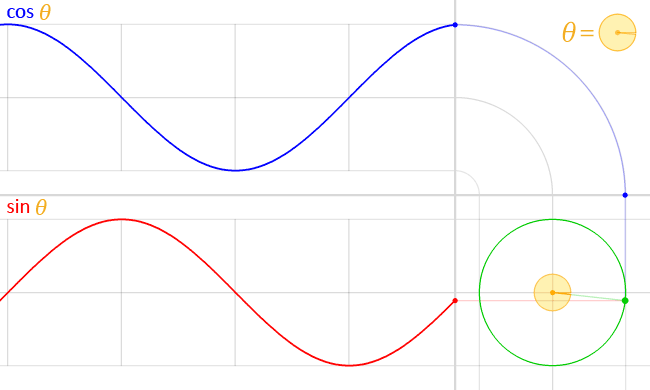
Conclusion: The particle moves counterclockwise around the unit circle, completing exactly one full revolution.
Transformations of the Unit Circle Parametric Function
The parametric function
\( (x(t), y(t)) = (\cos t, \sin t) \)
models a unit circle centered at the origin, traced counterclockwise as \( t \) increases.
By applying transformations to this parametric function, any circular path in the plane can be modeled.
A general parametric model for a circle is
\( (x(t), y(t)) = (a\cos t + h,\; a\sin t + k) \)
where:
• \( a \) is the radius of the circle
• \( (h, k) \) is the center of the circle
Changing the sign of \( t \) or replacing \( t \) with \( -t \) reverses the direction of traversal, while replacing \( t \) with \( bt \) changes the speed of motion.
Example:
Find a parametric equation for a circle of radius 3 centered at \( (2, -1) \), traversed counterclockwise.
▶️ Answer/Explanation
Start with the unit circle:
\( (\cos t, \sin t) \)
Apply a vertical and horizontal dilation by a factor of 3, then translate by \( (2, -1) \):
\( (x(t), y(t)) = (3\cos t + 2,\; 3\sin t – 1) \)
Conclusion: This parametric function models the required circular path.
Example:
Write parametric equations for a circle of radius 2 centered at the origin that is traversed clockwise.
▶️ Answer/Explanation
A counterclockwise circle of radius 2 is given by
\( (2\cos t,\; 2\sin t) \)
To reverse the direction, replace \( t \) with \( -t \):
\( (x(t), y(t)) = (2\cos t,\; -2\sin t) \)
Conclusion: This parametric function traces the same circle but in the clockwise direction.
Parametrizing a Linear Path Between Two Points
A linear path along the line segment from the point \( (x_1, y_1) \) to the point \( (x_2, y_2) \) can be described using a parametric function.
One common approach is to start at the initial position \( (x_1, y_1) \) and use constant rates of change for \( x \) and \( y \) with respect to the parameter \( t \).
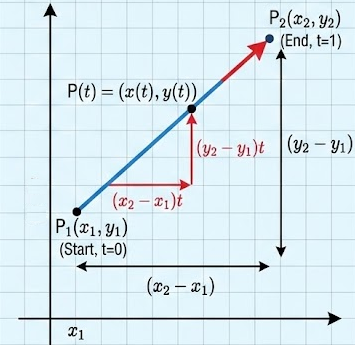
A standard parametrization of the line segment is
\( x(t) = x_1 + (x_2 – x_1)t,\quad y(t) = y_1 + (y_2 – y_1)t \)
with domain
\( 0 \le t \le 1 \)
Here, \( x_2 – x_1 \) and \( y_2 – y_1 \) represent the constant rates of change of \( x \) and \( y \), respectively.
Different parametrizations can be created by changing the interval for \( t \), reversing direction, or scaling the rates of change.
Example:
Parametrize the line segment from \( (1, 2) \) to \( (5, 6) \).
▶️ Answer/Explanation
Compute the rates of change:
\( x_2 – x_1 = 5 – 1 = 4,\quad y_2 – y_1 = 6 – 2 = 4 \)
Write the parametric equations:
\( x(t) = 1 + 4t,\quad y(t) = 2 + 4t,\quad 0 \le t \le 1 \)
Conclusion: As \( t \) increases from 0 to 1, the point moves linearly from \( (1,2) \) to \( (5,6) \).
Example:
A particle moves along the line segment from \( (-2, 3) \) to \( (4, -1) \) in 6 seconds. Find a parametrization using time \( t \), where \( 0 \le t \le 6 \).
▶️ Answer/Explanation
Compute the rates of change per second:
\( \dfrac{4 – (-2)}{6} = 1,\quad \dfrac{-1 – 3}{6} = -\dfrac{2}{3} \)
Write the parametric equations:
\( x(t) = -2 + t,\quad y(t) = 3 – \dfrac{2}{3}t,\quad 0 \le t \le 6 \)
Conclusion: This parametrization models uniform motion along the line segment over the given time interval.
