AP Precalculus -4.7 Parametrization of Implicit Functions- Study Notes - Effective Fall 2023
AP Precalculus -4.7 Parametrization of Implicit Functions- Study Notes – Effective Fall 2023
AP Precalculus -4.7 Parametrization of Implicit Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Represent a curve in the plane parametrically.
Represent conic sections parametrically.
Key Concepts:
Parametrization of an Implicitly Defined Function
Parametrizing Functions and Their Inverses
Parametrizing Parabolas
Parametrizing an Ellipse Using Trigonometric Functions
Parametrizing a Hyperbola Using Trigonometric Functions
Parametrization of an Implicitly Defined Function
An implicitly defined function is described by an equation involving two variables, such as \( F(x, y) = 0 \).
A parametrization of this relation is a pair of functions
\( (x(t), y(t)) \)
with the property that, when \( x(t) \) and \( y(t) \) are substituted for \( x \) and \( y \) in the original equation, the equation is satisfied for every value of \( t \) in the domain.
This means that each value of \( t \) produces a point \( (x(t), y(t)) \) that lies on the graph of the implicitly defined function.
Thus, a parametrization generates points on the curve without explicitly solving the equation for one variable in terms of the other.
Example:
Consider the implicit equation
\( x^2 + y^2 = 1 \)
Show that \( x(t) = \cos t \), \( y(t) = \sin t \) is a parametrization of this equation.
▶️ Answer/Explanation
Substitute \( x(t) \) and \( y(t) \) into the equation:
\( (\cos t)^2 + (\sin t)^2 = \cos^2 t + \sin^2 t \)
Using the Pythagorean identity,
\( \cos^2 t + \sin^2 t = 1 \)
This equality holds for all real values of \( t \).
Conclusion: The parametrization satisfies the implicit equation for every \( t \), so it represents the unit circle.
Example:
Verify that the parametric equations
\( x(t) = 2\cos t,\quad y(t) = 3\sin t \)
parametrize the ellipse
\( \dfrac{x^2}{4} + \dfrac{y^2}{9} = 1 \)
▶️ Answer/Explanation
Substitute \( x(t) \) and \( y(t) \) into the equation:
\( \dfrac{(2\cos t)^2}{4} + \dfrac{(3\sin t)^2}{9} \)
\( = \dfrac{4\cos^2 t}{4} + \dfrac{9\sin^2 t}{9} \)
\( = \cos^2 t + \sin^2 t = 1 \)
Conclusion: The parametrization satisfies the ellipse equation for all \( t \).
Parametrizing Functions and Their Inverses
If \( f \) is a function of \( x \), then its graph given by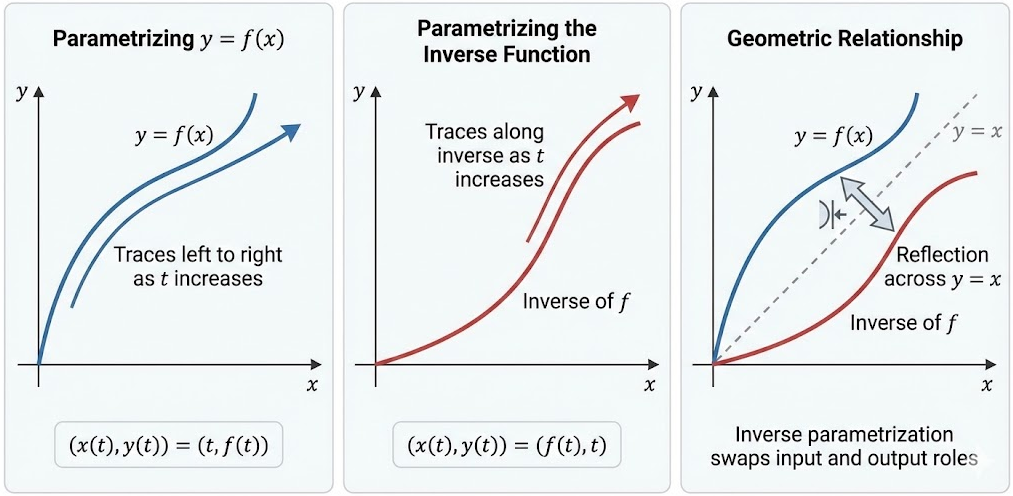
\( y = f(x) \)
can be written as a parametric function by letting the input variable itself be the parameter.
A standard parametrization of \( y = f(x) \) is
\( (x(t), y(t)) = (t, f(t)) \)
where \( t \) varies over the domain of \( f \). This parametrization traces the graph of the function from left to right as \( t \) increases.
If the function \( f \) is invertible, then its inverse function can also be parametrized.
A parametrization of the inverse function is obtained by swapping the roles of input and output:
\( (x(t), y(t)) = (f(t), t) \)
for an appropriate interval of \( t \). This corresponds to reflecting the graph of \( y = f(x) \) across the line \( y = x \).
Example:
Given the function \( f(x) = x^2 + 1 \), write a parametric representation of its graph.
▶️ Answer/Explanation
Use the standard parametrization \( (t, f(t)) \):
\( (x(t), y(t)) = (t, t^2 + 1) \)
As \( t \) varies over all real numbers, this parametrization traces the entire graph of \( y = x^2 + 1 \).
Conclusion: The parametric form represents the same curve as the original function.
Example:
Let \( f(x) = x^3 \). Parametrize the function and its inverse.
▶️ Answer/Explanation
Parametrization of \( y = f(x) \)
\( (x(t), y(t)) = (t, t^3) \)
Parametrization of the inverse
Since \( f(x) = x^3 \) is invertible, its inverse is \( f^{-1}(x) = \sqrt[3]{x} \).
\( (x(t), y(t)) = (t^3, t) \)
Conclusion: The second parametrization traces the graph of the inverse function, which is the reflection of the original graph across \( y = x \).
Parametrizing Parabolas
A parabola can be parametrized in the same way as any equation involving two variables that can be solved explicitly for one variable in terms of the other.
The choice of parametrization depends on whether the equation is solved for \( x \) or for \( y \).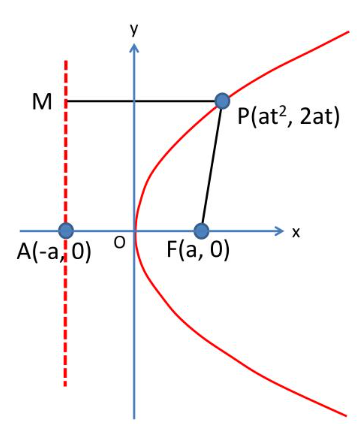
Parabolas solved for \( x \)
If the equation of the parabola can be written in the form
\( x = f(y) \)
then a parametrization is obtained by replacing \( y \) with the parameter \( t \):
\( (x(t), y(t)) = (f(t), t) \)
Parabolas solved for \( y \)
If the equation of the parabola can be written in the form
\( y = f(x) \)
then a parametrization is obtained by replacing \( x \) with the parameter \( t \):
\( (x(t), y(t)) = (t, f(t)) \)
In both cases, substituting \( x(t) \) and \( y(t) \) into the original equation satisfies the equation for all values of \( t \) in the chosen domain.
Example:
Parametrize the parabola
\( y = x^2 \)
▶️ Answer/Explanation
Since the equation is solved for \( y \), replace \( x \) with \( t \):
\( (x(t), y(t)) = (t, t^2) \)
As \( t \) varies over all real numbers, this parametrization traces the entire parabola.
Conclusion: This is a valid parametrization of the parabola.
Example:
Parametrize the parabola
\( x = 2y^2 – 1 \)
▶️ Answer/Explanation
Since the equation is solved for \( x \), replace \( y \) with \( t \):
\( (x(t), y(t)) = (2t^2 – 1, t) \)
Substituting into the original equation confirms the parametrization.
Conclusion: This parametrization traces the parabola from bottom to top as \( t \) increases.
Parametrizing an Ellipse Using Trigonometric Functions
An ellipse centered at \( (h, k) \) with horizontal radius \( a \) and vertical radius \( b \) can be parametrized using trigonometric functions.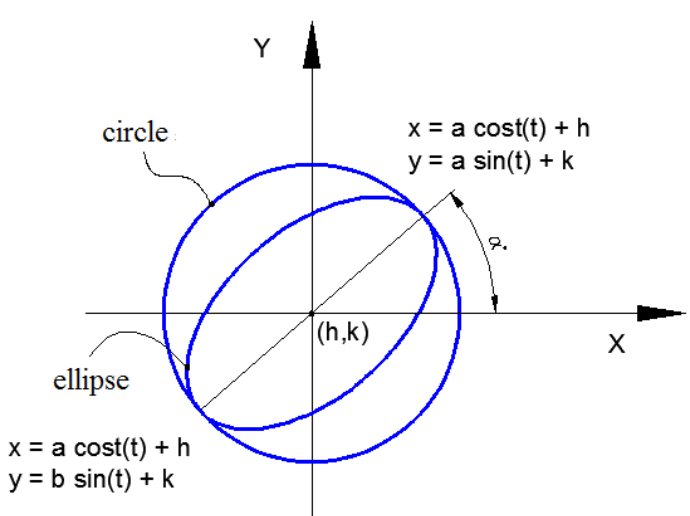
A standard parametrization of the ellipse is
\( x(t) = h + a\cos t \)
\( y(t) = k + b\sin t \)
with domain
\( 0 \le t \le 2\pi \)
This parametrization works because \( \cos t \) and \( \sin t \) trace the unit circle, and the factors \( a \) and \( b \) stretch the circle horizontally and vertically to form an ellipse.
Substituting \( x(t) \) and \( y(t) \) into the standard ellipse equation
\( \dfrac{(x – h)^2}{a^2} + \dfrac{(y – k)^2}{b^2} = 1 \)
shows that the equation is satisfied for all \( t \) in the interval.
As \( t \) increases from \( 0 \) to \( 2\pi \), the ellipse is traced exactly once in the counterclockwise direction.
Example:
Parametrize the ellipse centered at \( (0, 0) \) with horizontal radius 4 and vertical radius 2.
▶️ Answer/Explanation
Here, \( h = 0 \), \( k = 0 \), \( a = 4 \), and \( b = 2 \).
The parametrization is
\( x(t) = 4\cos t \)
\( y(t) = 2\sin t \), \( 0 \le t \le 2\pi \)
Conclusion: These equations trace the ellipse exactly once as \( t \) varies from 0 to \( 2\pi \).
Example:
Show that the parametrization
\( x(t) = 3 + 5\cos t,\quad y(t) = -1 + 2\sin t \)
represents an ellipse, and identify its center and radii.
▶️ Answer/Explanation
Compare with the standard form
\( x(t) = h + a\cos t,\quad y(t) = k + b\sin t \)
This gives
\( h = 3,\quad k = -1,\quad a = 5,\quad b = 2 \)
Substituting into the ellipse equation confirms
\( \dfrac{(x – 3)^2}{25} + \dfrac{(y + 1)^2}{4} = 1 \)
Conclusion: The parametrization represents an ellipse centered at \( (3, -1) \) with horizontal radius 5 and vertical radius 2.
Parametrizing a Hyperbola Using Trigonometric Functions
A hyperbola centered at \( (h, k) \) can be parametrized using trigonometric functions so that every point generated by the parametrization satisfies the hyperbola’s equation.
The specific parametrization depends on whether the hyperbola opens left and right or up and down.
Hyperbola opening left and right
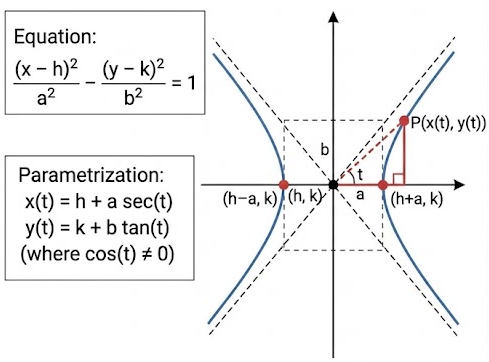
For a hyperbola with equation
\( \dfrac{(x – h)^2}{a^2} – \dfrac{(y – k)^2}{b^2} = 1 \)
a trigonometric parametrization is
\( x(t) = h + a\sec t \)
\( y(t) = k + b\tan t \)
where \( t \) is chosen so that \( \cos t \neq 0 \).
Hyperbola opening up and down
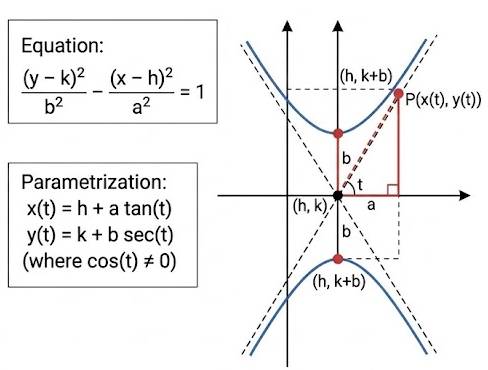
For a hyperbola with equation
\( \dfrac{(y – k)^2}{b^2} – \dfrac{(x – h)^2}{a^2} = 1 \)
a trigonometric parametrization is
\( x(t) = h + a\tan t \)
\( y(t) = k + b\sec t \)
again with \( \cos t \neq 0 \).
These parametrizations work because the trigonometric identity
\( \sec^2 t – \tan^2 t = 1 \)
ensures that substituting \( x(t) \) and \( y(t) \) into the hyperbola’s equation satisfies it for every allowable value of \( t \).
Example:
Parametrize the hyperbola
\( \dfrac{x^2}{9} – \dfrac{y^2}{4} = 1 \)
▶️ Answer/Explanation
This hyperbola opens left and right with \( a = 3 \), \( b = 2 \), and center \( (0,0) \).
A parametrization is
\( x(t) = 3\sec t,\quad y(t) = 2\tan t \)
Substituting confirms
\( \dfrac{(3\sec t)^2}{9} – \dfrac{(2\tan t)^2}{4} = \sec^2 t – \tan^2 t = 1 \)
Conclusion: This parametrization traces the hyperbola for all valid values of \( t \).
Example:
Parametrize the hyperbola centered at \( (1, -2) \) given by
\( \dfrac{(y + 2)^2}{16} – \dfrac{(x – 1)^2}{25} = 1 \)
▶️ Answer/Explanation
This hyperbola opens up and down with \( a = 5 \) and \( b = 4 \).
A parametrization is
\( x(t) = 1 + 5\tan t,\quad y(t) = -2 + 4\sec t \)
Conclusion: For all \( t \) with \( \cos t \neq 0 \), these equations generate points on the hyperbola.
