AP Precalculus -4.9 Vector-Valued Functions- Study Notes - Effective Fall 2023
AP Precalculus -4.9 Vector-Valued Functions- Study Notes – Effective Fall 2023
AP Precalculus -4.9 Vector-Valued Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Represent planar motion in terms of vector-valued functions.
Key Concepts:
Position Vectors and Vector-Valued Functions
Velocity as a Vector-Valued Function
Position Vectors and Vector-Valued Functions
The position of a particle moving in a plane can be described using a parametric function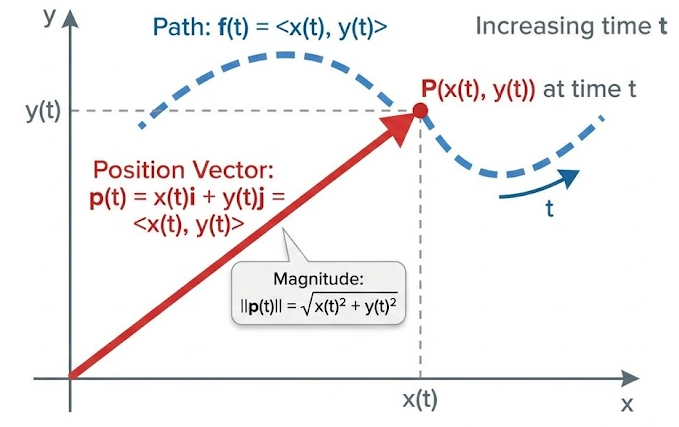
\( f(t) = \langle x(t), y(t) \rangle \)
This same motion can be represented as a vector-valued function, called the position vector.
The position vector is written as
\( \mathbf{p}(t) = x(t)\mathbf{i} + y(t)\mathbf{j} \)
or equivalently as
\( \mathbf{p}(t) = \langle x(t), y(t) \rangle \)
Each value of \( t \) determines a vector that starts at the origin and points to the location of the particle at time \( t \).
The magnitude of the position vector gives the distance of the particle from the origin and is found using
\( \lVert \mathbf{p}(t) \rVert = \sqrt{x(t)^2 + y(t)^2} \)
This value represents how far the particle is from the origin at time \( t \).
Example:
A particle moves according to
\( x(t) = 3t,\quad y(t) = 4t \)
Write the position vector and find the distance of the particle from the origin at time \( t \).
▶️ Answer/Explanation
The position vector is
\( \mathbf{p}(t) = \langle 3t, 4t \rangle \)
Its magnitude is
\( \lVert \mathbf{p}(t) \rVert = \sqrt{(3t)^2 + (4t)^2} = \sqrt{9t^2 + 16t^2} = \sqrt{25t^2} = 5|t| \)
Conclusion: The particle is \( 5|t| \) units from the origin at time \( t \).
Example:
A particle moves along a circle according to
\( x(t) = 2\cos t,\quad y(t) = 2\sin t \)
Write the position vector and describe the particle’s distance from the origin.
▶️ Answer/Explanation
The position vector is
\( \mathbf{p}(t) = \langle 2\cos t, 2\sin t \rangle \)
Its magnitude is
\( \lVert \mathbf{p}(t) \rVert = \sqrt{(2\cos t)^2 + (2\sin t)^2} = \sqrt{4(\cos^2 t + \sin^2 t)} = \sqrt{4} = 2 \)
Conclusion: The particle remains exactly 2 units from the origin at all times, so it moves along a circle of radius 2.
Velocity as a Vector-Valued Function
For a particle moving in a plane, the velocity at time \( t \) can be represented using a vector-valued function.
If the position of the particle is given by the parametric function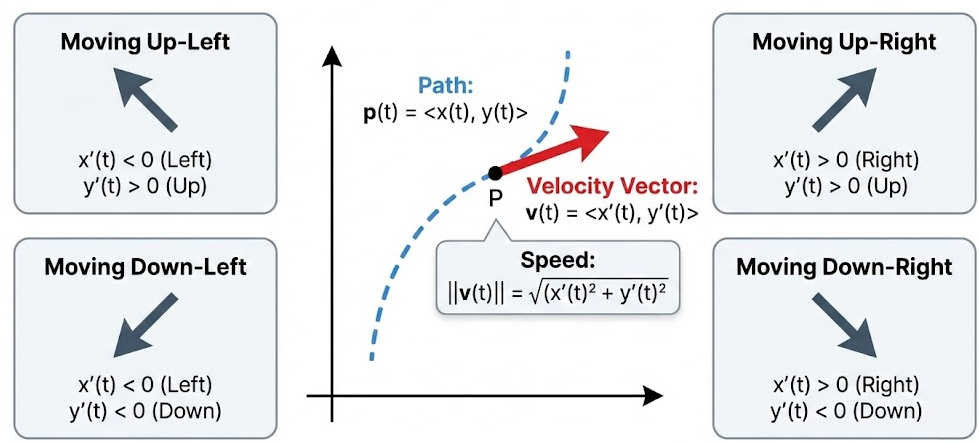
\( \mathbf{p}(t) = \langle x(t), y(t) \rangle \),
then the velocity vector is written as
\( \mathbf{v}(t) = \langle x(t), y(t) \rangle \).
At any time \( t \):
• If \( x(t) > 0 \), the particle is moving to the right; if \( x(t) < 0 \), it is moving to the left.
• If \( y(t) > 0 \), the particle is moving upward; if \( y(t) < 0 \), it is moving downward.
The speed of the particle at time \( t \) is the magnitude of the velocity vector and is given by
\( \lVert \mathbf{v}(t) \rVert = \sqrt{x(t)^2 + y(t)^2} \).
Speed is a scalar quantity and measures how fast the particle is moving, regardless of direction.
Example:
A particle has velocity
\( \mathbf{v}(t) = \langle 3, -4 \rangle \).
Describe the direction of motion and find the speed.
▶️ Answer/Explanation
Since \( x(t) = 3 > 0 \), the particle moves to the right.
Since \( y(t) = -4 < 0 \), the particle moves downward.
The speed is
\( \lVert \mathbf{v}(t) \rVert = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = 5 \).
Conclusion: The particle moves down and to the right with speed 5 units per unit time.
Example:
A particle’s velocity is given by
\( \mathbf{v}(t) = \langle -2t, t \rangle \).
Determine the direction of motion and speed at \( t = 2 \).
▶️ Answer/Explanation
At \( t = 2 \),
\( \mathbf{v}(2) = \langle -4, 2 \rangle \).
Since the \( x \)-component is negative, the particle moves left.
Since the \( y \)-component is positive, the particle moves upward.
The speed is
\( \lVert \mathbf{v}(2) \rVert = \sqrt{(-4)^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20} \).
Conclusion: At \( t = 2 \), the particle moves up and to the left with speed \( \sqrt{20} \).
