A jewelry company uses a machine to apply a coating of gold on a certain style of necklace. The amount of gold applied to a necklace is approximately normally distributed. When the machine is working properly, the amount of gold applied to a necklace has a mean of \(300\) milligrams (mg) and standard deviation of \(5\) mg.
(a) A necklace is randomly selected from the necklaces produced by the machine. Assuming that the machine is working properly, calculate the probability that the amount of gold applied to the necklace is between \(296\) mg and \(304\) mg.
The jewelry company wants to make sure the machine is working properly. Each day, Cleo, a statistician at the jewelry company, will take a random sample of the necklaces produced that day. Each selected necklace will be melted down and the amount of the gold applied to that necklace will be determined. Because a necklace must be destroyed to determine the amount of gold that was applied, Cleo will use random samples of size \(n=2\) necklaces.
Cleo starts by considering the mean amount of gold being applied to the necklaces. After Cleo takes a random sample of \(n=2\) necklaces, she computes the sample mean amount of gold applied to the two necklaces.
(b) Suppose the machine is working properly with a population mean amount of gold being applied of \(300\) mg and a population standard deviation of \(5\) mg.
(i) Calculate the probability that the sample mean amount of gold applied to a random sample of \(n=2\) necklaces will be greater than \(303\) mg.
(ii) Suppose Cleo took a random sample of \(n=2\) necklaces that resulted in a sample mean amount of gold applied of \(303\) mg. Would that result indicate that the population mean amount of gold being applied by the machine is different from \(300\) mg? Justify your answer without performing an inference procedure.
Now, Cleo will consider the variation in the amount of gold the machine applies to the necklaces. Because of the small sample size, \(n=2\), Cleo will use the sample range of the data for the two randomly selected necklaces, rather than the sample standard deviation.
Cleo will investigate the behavior of the range for samples of size \(n=2\). She will simulate the sampling distribution of the range of the amount of gold applied to two randomly sampled necklaces. Cleo generates \(100,000\) random samples of size \(n=2\) independent values from a normal distribution with mean \(\mu=300\) and standard deviation \(\sigma=5\). The range is calculated for the two observations in each sample. The simulated sampling distribution of the range is shown in Graph I. This process is repeated using \(\sigma=8\), as shown in Graph II, and again using \(\sigma=12\), as shown in Graph III.
(c) Use the information in the graphs to complete the following.
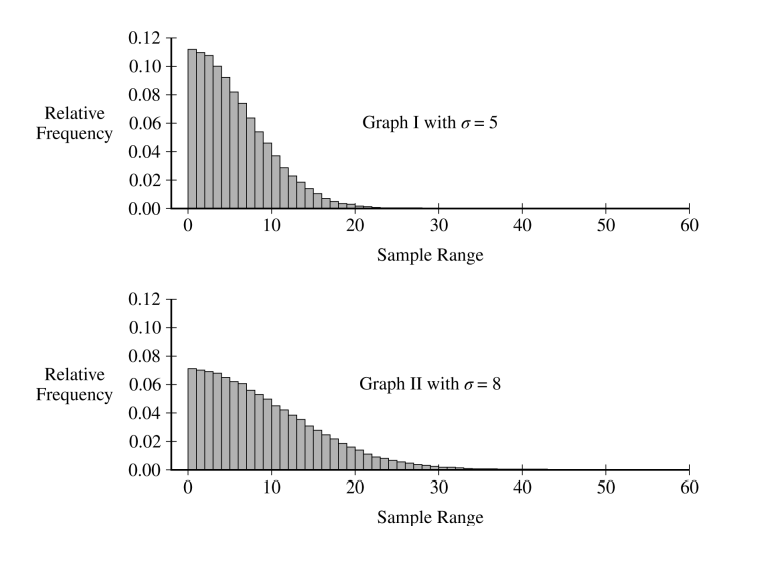
(i) Describe the sampling distribution of the sample range for random samples of size \(n=2\) from a normal distribution with standard deviation \(\sigma=5\), as shown in Graph I.
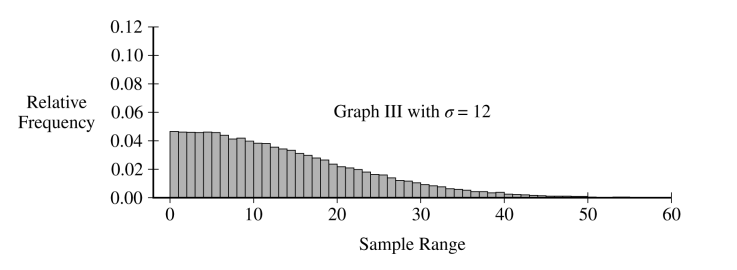
(ii) Describe how the sampling distribution of the sample range for samples of size \(n=2\) changes as the value of the population standard deviation increases.
Recall that Cleo needs to consider both the mean and standard deviation of the amount of gold applied to necklaces to determine whether the machine is working properly. Suppose that one month later, Cleo is again checking the machine to make sure it is working properly. Cleo takes a random sample of \(2\) necklaces and calculates the sample mean amount of gold applied as \(303\) mg and the sample range as \(10\) mg.
(d) Recall that the machine is working properly if the amount of gold applied to the necklaces has a mean of \(300\) mg and standard deviation of \(5\) mg.
(i) Consider Cleo’s range of \(10\) mg from the sample of size \(n=2\). If the machine is working properly with a standard deviation of \(5\) mg, is a sample range of \(10\) mg unusual? Justify your answer.
(ii) Do Cleo’s sample mean of \(303\) mg and range of \(10\) mg indicate that the machine is not working properly? Explain your answer.
Most-appropriate topic codes (CED):
• TOPIC 1.10 — The Normal Distribution: (a)
• TOPIC 5.7 — Sampling Distributions for Sample Means: (b)(i), (b)(ii), (d)(ii)
• TOPIC 5.1 — Introducing Statistics: Why Is My Sample Not Like Yours?: (c)(i), (c)(ii), (d)(i), (d)(ii)
