AP Statistics 5.3 The Central Limit Theorem- FRQs - Exam Style Questions
Question
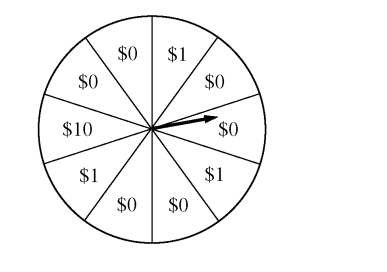
| \( x \) | \( \$2 \) | \( \$1 \) | \( -\$8 \) |
|---|---|---|---|
| \( P(x) \) |
Most-appropriate topic codes (CED):
• TOPIC 4.8: Mean and Standard Deviation of Random Variables — part (b)
• TOPIC 4.8: Mean and Standard Deviation of Random Variables — part (c)
• TOPIC 5.3: The Central Limit Theorem — part (d)
▶️ Answer/Explanation
(a)
Counting the sectors: \( \$2 \) appears in \( 6 \) sectors, \( \$1 \) appears in \( 3 \) sectors, and \( -\$8 \) appears in \( 1 \) sector.
Thus: \( P(\$2) = \frac{6}{10} = 0.6 \), \( P(\$1) = \frac{3}{10} = 0.3 \), \( P(-\$8) = \frac{1}{10} = 0.1 \).
\[ \boxed{\begin{array}{|c|c|c|c|} \hline x & \$2 & \$1 & -\$8 \\ \hline P(x) & 0.6 & 0.3 & 0.1 \\ \hline \end{array}} \]
(b)
\[E(X) = \$2(0.6) + \$1(0.3) + (-\$8)(0.1) = \$1.20 + \$0.30 – \$0.80 = \$0.70\]
\(\boxed{\$0.70}\)
(c)
Let \( n \) be the number of plays. Expected contribution \( = 0.70n \).
Set \( 0.70n \geq 500 \) ⇒ \( n \geq \frac{500}{0.70} \approx 714.286 \).
The smallest integer greater than \( 714.286 \) is \( 715 \).
\(\boxed{715}\)
(d)
Let \( S \) be the total net contribution from \( 1,000 \) plays.
\( S \) is approximately normal with mean \( \mu = 700 \) and standard deviation \( \sigma = 92.79 \).
We want \( P(S \geq 500) \).
Compute \( z = \frac{500 – 700}{92.79} \approx -2.155 \).
\( P(S \geq 500) = P(Z \geq -2.155) = 1 – P(Z < -2.155) \approx 1 – 0.0156 = 0.9844 \).
\(\boxed{0.9844}\)
