1.1B Measurement Precision and Experimental Data- Pre AP Chemistry Study Notes - New Syllabus.
1.1B Measurement Precision and Experimental Data- Pre AP Chemistry Study Notes
1.1B Measurement Precision and Experimental Data- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
1.1.B.1 Justify the choice of equipment used to make a measurement, based on precision.
1.1.B.2 Record measured values to the proper experimental precision.
Key Concepts:
- 1.1.B Recorded values must account for the precision of a measurement.
a. The precision of a measurement is limited by the precision of the instrument used to make the measurement.
b. Recorded values should include one estimated digit beyond the scale of the instrument used to make the measurement.
1.1.B.1 — Precision, Measurement, and Choice of Equipment
In chemistry, measurements must be both appropriate and precise. The choice of equipment determines how precisely a quantity can be measured and how the value must be recorded.
A measurement is only as precise as the instrument used to make it. This idea is central to making valid scientific measurements and recording data correctly.
What Is Precision?
Precision describes how finely a measuring instrument can distinguish between values. It depends on the smallest scale division on the instrument.
- An instrument with smaller scale divisions has higher precision
- Precision is about detail and resolution, not correctness
- Precision limits the number of digits that can be recorded
Justifying the Choice of Equipment
To justify the choice of equipment, consider:

- The quantity being measured (length, mass, volume, temperature)
- The required level of precision
- The scale markings of the instrument
Scientists choose the most precise instrument that is reasonable for the task. Using an instrument with insufficient precision limits data quality.
Examples of Equipment and Precision
| Quantity Measured | Instrument | Typical Precision |
|---|---|---|
| Length | Ruler (mm scale) | \( \mathrm{\pm 0.1\ cm} \) |
| Mass | Digital balance | \( \mathrm{\pm 0.01\ g} \) |
| Volume | Graduated cylinder | \( \mathrm{\pm 0.5\ mL} \) |
| Temperature | Thermometer | \( \mathrm{\pm 0.1\ ^\circ C} \) |
Recorded Values and Instrument Precision
Recorded values must reflect the precision of the instrument used. This means:
- All certain digits are recorded
- One estimated digit is recorded beyond the smallest scale division
- No extra digits are added
Recording more digits than the instrument allows gives a false sense of precision.
Key Rule
The precision of a measurement is limited by the precision of the instrument, not by the skill of the person measuring.
Example
A student measures the mass of a sample using a balance that reads to the nearest 0.01 g. The display shows 12.34 g. Explain why this recording is appropriate.
▶️ Answer / Explanation
The balance has a precision of 0.01 g, so the mass should be recorded to two decimal places. Writing 12.34 g reflects the maximum precision of the instrument.
Example
You need to measure exactly 25.0 mL of a liquid for an experiment. Justify why a graduated cylinder is a better choice than a beaker.
▶️ Answer / Explanation
A graduated cylinder has finer scale markings than a beaker, allowing volume to be measured with greater precision. Since the value must be recorded as 25.0 mL, the instrument must support measurement to the nearest 0.1 mL, which a beaker cannot reliably provide.
1.1.B.2 — Recording Measurements to Proper Experimental Precision
In scientific measurements, it is not enough to choose the correct instrument. Measurements must be recorded correctly so that they accurately reflect the precision of the instrument.
Correct recording of measured values ensures that data are reliable, comparable, and scientifically valid.
Experimental Precision and Recorded Values
Experimental precision refers to how finely a measurement can be reported, based on the scale markings of the measuring instrument.
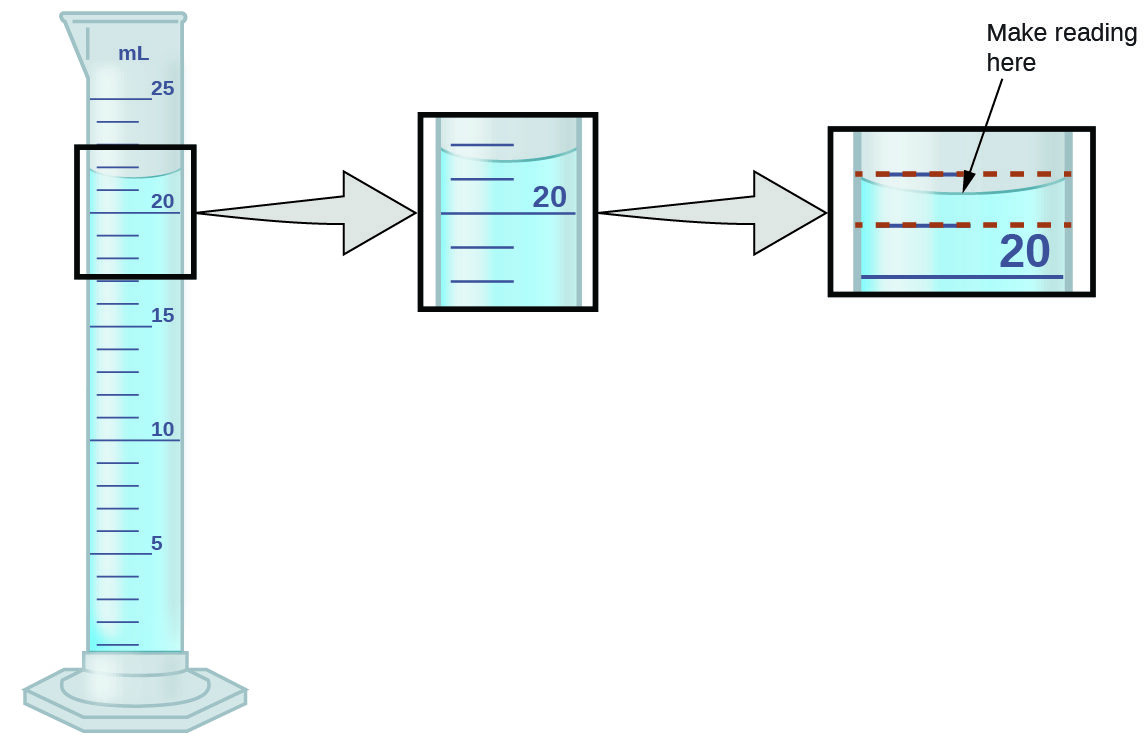
A recorded measurement must:
- Include all certain digits shown by the instrument
- Include one estimated digit beyond the smallest scale marking
- Include no additional digits
The Estimated Digit Rule
Recorded values should include one estimated digit beyond the scale of the instrument.
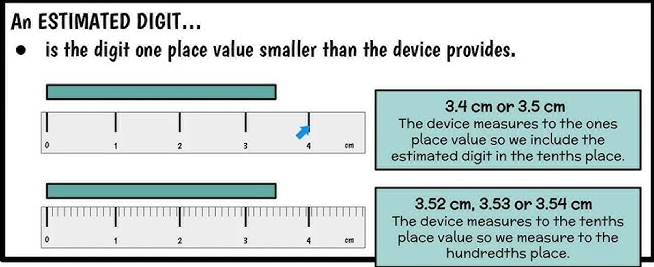
The estimated digit:
- Is the last digit in the recorded value
- Represents the observer’s best judgment
- Adds meaningful precision without overstating accuracy
Even though this digit is estimated, it is still required for proper scientific reporting.
How to Determine the Correct Number of Digits

Follow these steps when recording a measurement:
- Identify the smallest scale division on the instrument
- Record all digits up to that scale marking
- Estimate one additional digit beyond that marking
You may estimate only one digit. Estimating more than one digit creates false precision.
Examples of Properly Recorded Measurements
| Instrument | Smallest Scale Division | Correct Recording |
|---|---|---|
| Ruler | \( \mathrm{1\ mm} \) | \( \mathrm{12.4\ cm} \) |
| Graduated cylinder | \( \mathrm{1\ mL} \) | \( \mathrm{36.7\ mL} \) |
| Digital balance | \( \mathrm{0.01\ g} \) | \( \mathrm{8.32\ g} \) |
Common Errors to Avoid
- Recording too many digits (overstating precision)
- Rounding early instead of recording the estimated digit
- Leaving off the estimated digit entirely
Any of these mistakes can make experimental data misleading or unusable.
Example
A graduated cylinder has markings every 1 mL. The liquid level is slightly above 42 mL. Record the volume correctly.
▶️ Answer / Explanation
The smallest scale division is 1 mL, so one digit beyond this must be estimated.
A correct recording is \( \mathrm{42.3\ mL} \) (any reasonable estimated digit between 42.1 and 42.9 mL is acceptable).
Example
A student records the length of a metal strip as \( \mathrm{15.237\ cm} \) using a ruler marked in millimeters. Evaluate whether this measurement is recorded correctly and justify your answer.
▶️ Answer / Explanation
The measurement is not recorded correctly.
A ruler marked in millimeters allows recording to the nearest 0.1 cm (one estimated digit). Recording four decimal places greatly exceeds the instrument’s precision and creates false precision. A correct recording would be approximately \( \mathrm{15.2\ cm} \).
