1.1C Density and Particle Packing- Pre AP Chemistry Study Notes - New Syllabus.
1.1C Density and Particle Packing- Pre AP Chemistry Study Notes
1.1C Density and Particle Packing- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
1.1.C.1 Create and/or evaluate particulate and graphical models representing the density of pure substances.
1.1.C.2 Explain the relationship between the density and the arrangement of particles within a puresubstance.
1.1.C.3 Perform calculations relating to the density of pure substances.
Key Concepts:
- 1.1.C Density is a quantitative measure of the packing of particles that make up matter.
a. The density of a substance is related to the mass of the particles that make up that substance and to how tightly these particles are packed.
b. The density of a substance can be represented by the slope of the line on a graph that plots the mass of the substance versus its volume.
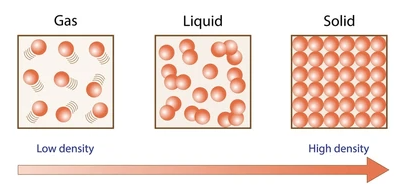
c. The density of a gas is substantially lower than that of either a solid or a liquid
1.1.C.1 — Particulate and Graphical Models of Density
Density describes how much matter is packed into a given amount of space. It is a characteristic property of a pure substance and does not depend on the amount of the substance present.
Scientists use both particulate models and graphical models to represent and compare the density of substances.
What Is Density?
Density is defined as the ratio of mass to volume:
\( \mathrm{density = \dfrac{mass}{volume}} \)
For pure substances, density remains constant under the same conditions of temperature and pressure.
Particulate Models of Density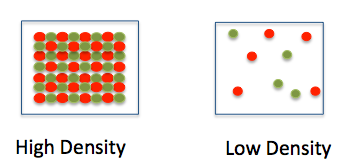
Particulate models show how particles are arranged within a fixed volume. Density is represented by how closely packed the particles are.
- Higher density → particles are more closely packed
- Lower density → particles are more spread out
- Particle size does not change in correct models
When evaluating a particulate model, focus on the number of particles in the same volume, not their appearance.
Comparing Density Using Particulate Models
| Model Feature | Lower Density | Higher Density |
|---|---|---|
| Particle spacing | Farther apart | Closer together |
| Particles per volume | Fewer | More |
| Volume shown | Same | Same |
Graphical Models of Density
Density can also be represented using graphs, most commonly mass vs. volume graphs.
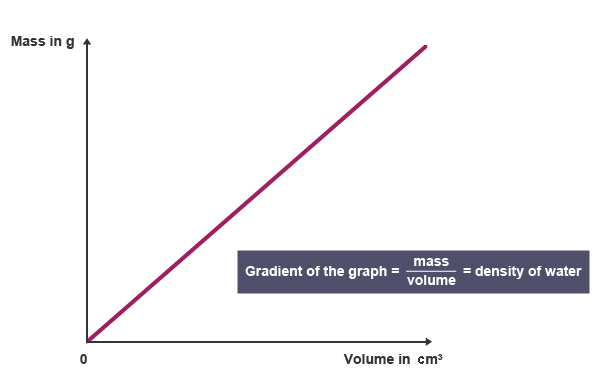
For a pure substance:
- The graph is a straight line through the origin
- The slope of the line represents density
A steeper slope indicates a greater mass per unit volume and therefore a higher density.
Interpreting Density Graphs
| Graph Feature | Meaning |
|---|---|
| Straight line | Constant density |
| Steeper slope | Higher density |
| Shallower slope | Lower density |
Evaluating Models of Density
A correct density model must:
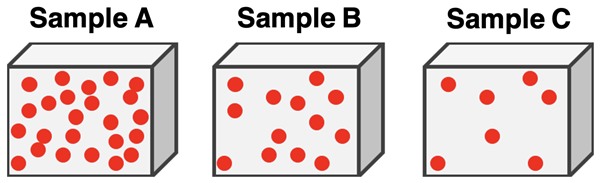
- Use the same volume when comparing substances
- Show differences in particle number or spacing
- Represent constant density for pure substances
Models that change particle size or volume while comparing density are incorrect.
Example
Two particulate models show the same volume. Model A contains fewer particles than Model B. Identify which substance has the greater density and explain your reasoning.
▶️ Answer / Explanation
Model B has the greater density.
Density depends on how much mass is packed into a given volume. Since Model B contains more particles in the same volume, it represents a substance with greater density.
Example
A mass vs. volume graph shows two straight lines for substances X and Y. Substance X has a steeper slope than substance Y. Using both graphical and particulate reasoning, explain which substance has the higher density.
▶️ Answer / Explanation
Substance X has the higher density.
On a mass vs. volume graph, the slope represents density. A steeper slope means more mass per unit volume. In a particulate model, this corresponds to more particles packed into the same volume compared to substance Y.
1.1.C.2 — Density and Particle Arrangement in Pure Substances
The density of a pure substance is determined by how its particles are arranged within a given volume. Because a pure substance has the same type of particles throughout, its density reflects a consistent particle arrangement under the same conditions.
Density and Particle Arrangement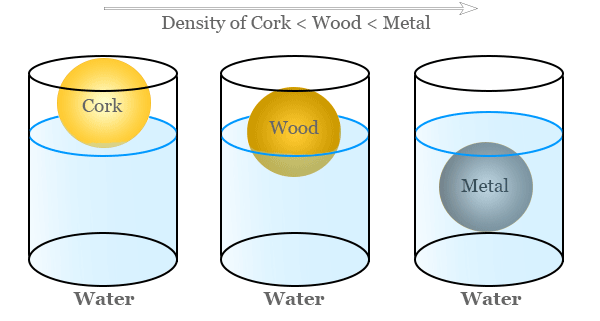
Density measures how much mass is packed into a specific volume. In particle terms, this depends on:
- How many particles occupy the volume
- How closely packed the particles are
- The mass of each particle
For a pure substance, particle mass is constant, so density differences come from particle spacing and arrangement.
High Density Substances
A pure substance has a high density when many particles are packed closely together in a fixed volume.
- Particles are very close together
- There is little empty space between particles
- Strong attractive forces often pull particles closer

This arrangement results in more mass per unit volume.
Low Density Substances
A pure substance has a low density when particles are more spread out within the same volume.
- Particles are farther apart
- There is more empty space between particles
- Fewer particles occupy a given volume
This arrangement results in less mass per unit volume.
Why Density Is Constant for a Pure Substance
Because a pure substance has identical particles arranged in the same way, its density remains constant as long as temperature and pressure are unchanged.
Changing the amount of the substance changes both mass and volume proportionally, so the ratio (density) stays the same.
Particle Arrangement and Density Comparison
| Particle Arrangement | Density Effect |
|---|---|
| Particles packed closely | High density |
| Particles more spread out | Low density |
Evaluating Particle Models
When evaluating a particulate model of a pure substance, a correct explanation of density must:
- Keep particle size constant
- Compare equal volumes
- Focus on spacing and number of particles
Models that change particle size instead of spacing do not correctly represent density differences.
Example
Explain why a solid is usually denser than a gas using particle arrangement.
▶️ Answer / Explanation
In a solid, particles are tightly packed with very little empty space, so many particles occupy a small volume. In a gas, particles are far apart with large amounts of empty space, resulting in much less mass in the same volume.
Example
Two samples of the same pure substance are shown using particulate models. One sample shows particles closer together than the other. Explain how temperature could account for this difference while the density remains constant.
▶️ Answer / Explanation
An increase in temperature causes particles to move faster and spread slightly farther apart, increasing volume. Although particle spacing increases, mass and volume change proportionally, so the ratio of mass to volume (density) remains constant for the pure substance under the same conditions.
1.1.C.3 — Density Calculations for Pure Substances
Calculations involving density allow scientists to quantitatively compare pure substances and predict behaviors such as floating, sinking, and material identification.
Because density is a characteristic property of a pure substance, correct calculations depend on using consistent units and proper experimental precision.
Density Formula
Density is defined as mass divided by volume:
\( \mathrm{density = \dfrac{mass}{volume}} \)
Common units:
- Density: \( \mathrm{g\,cm^{-3}} \) or \( \mathrm{g\,mL^{-1}} \)
- Mass: \( \mathrm{g} \)
- Volume: \( \mathrm{cm^{3}} \) or \( \mathrm{mL} \)
Note that \( \mathrm{1\ cm^{3} = 1\ mL} \).
Rearranging the Density Equation![]()
The density equation can be rearranged to calculate mass or volume:
\( \mathrm{mass = density \times volume} \)
\( \mathrm{volume = \dfrac{mass}{density}} \)
Choose the form of the equation based on the quantity you are solving for.
Steps for Density Calculations
- Write the correct density equation
- Substitute given values with units
- Check unit consistency
- Calculate the value
- Round to the correct experimental precision
Example
A metal sample has a mass of \( \mathrm{54.0\ g} \) and a volume of \( \mathrm{20.0\ cm^{3}} \). Calculate its density.
▶️ Answer / Explanation
Use the density formula:
\( \mathrm{density = \dfrac{54.0}{20.0}} \)
\( \mathrm{density = 2.70\ g\,cm^{-3}} \)
The density of the metal is \( \mathrm{2.70\ g\,cm^{-3}} \).
Example
A pure liquid has a density of \( \mathrm{0.789\ g\,mL^{-1}} \). What mass of the liquid is contained in a volume of \( \mathrm{125.0\ mL} \)?
▶️ Answer / Explanation
Use the mass equation:
\( \mathrm{mass = density \times volume} \)
\( \mathrm{mass = 0.789 \times 125.0} \)
\( \mathrm{mass = 98.6\ g} \)
The mass of the liquid is \( \mathrm{98.6\ g} \), rounded to the correct precision.