1.2A Thermal Energy and Heat Capacity- Pre AP Chemistry Study Notes - New Syllabus.
1.2A Thermal Energy and Heat Capacity- Pre AP Chemistry Study Notes
1.2A Thermal Energy and Heat Capacity- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
1.2.A.1 Create and/or evaluate a claim about the relationship between transfer of thermal energy and the temperature change in different samples.
1.2.A.2 Perform calculations using data gathered from a simple constant-pressure calorimetry experiment.
Key Concepts:
- 1.2.A The transfer of energy associated with a change in temperature of a sample of matter is heat. Specific heat capacity is a proportionality constant that relates the amount of energy absorbed by a substance to its mass and its change in temperature.
1.2.A.1 — Thermal Energy Transfer and Temperature Change
Thermal energy transfer affects the temperature of a substance, but the size of the temperature change depends on the properties of the sample. Scientists make and evaluate claims about this relationship by comparing how different samples respond when the same amount of thermal energy is transferred.
Thermal Energy vs. Temperature
Thermal energy is the total kinetic energy of all particles in a substance, while temperature is a measure of the average kinetic energy of those particles.
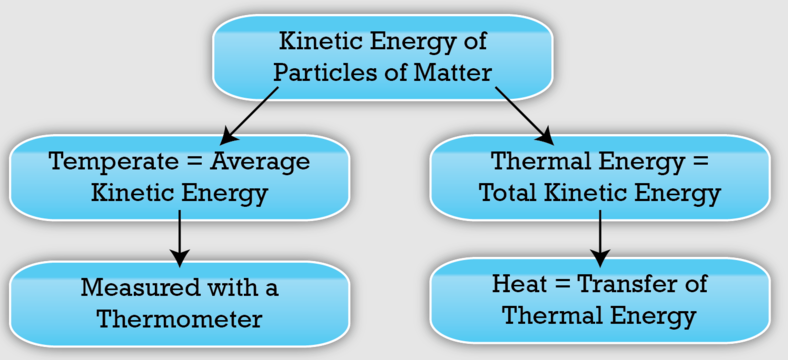
Because of this difference:
- Adding the same thermal energy to different substances can result in different temperature changes
- Larger samples may experience smaller temperature changes than smaller samples
Claim: Relationship Between Thermal Energy Transfer and Temperature Change
A valid scientific claim is:
When the same amount of thermal energy is transferred to different samples, the temperature change depends on the mass and the type of substance.
This claim is supported by particle behavior and experimental observations.
Effect of Mass on Temperature Change
For samples of the same substance:
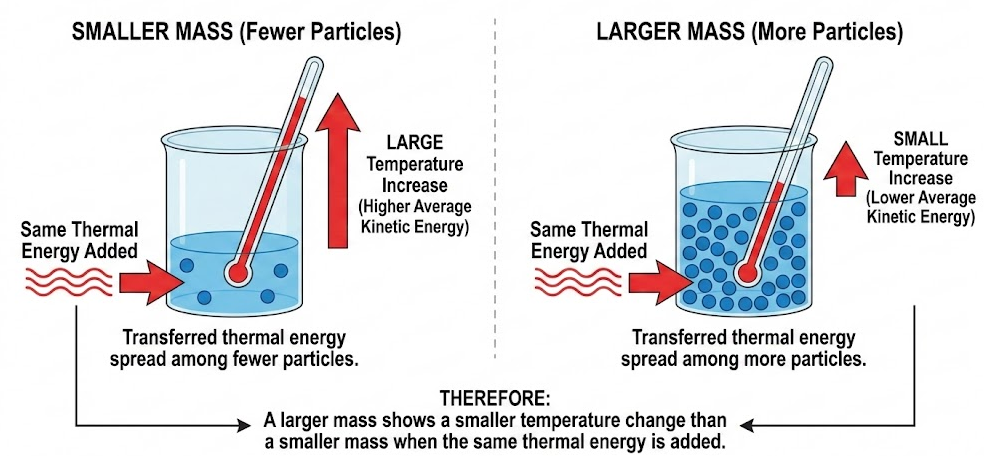
- A larger mass contains more particles
- Transferred thermal energy is spread among more particles
- The average kinetic energy (temperature) increases less
Therefore, a larger mass shows a smaller temperature change than a smaller mass when the same thermal energy is added.
Effect of Substance Type on Temperature Change
Different substances respond differently to the same thermal energy transfer. This is related to the substance’s ability to absorb thermal energy.
![]()
- Some substances require more energy to increase temperature
- Others increase temperature more easily
As a result, two samples with the same mass can experience different temperature changes when given the same amount of thermal energy.
Evaluating Claims Using Models
Particle models help evaluate claims by showing:
- The number of particles in each sample
- How transferred energy is distributed among particles
- Differences in particle motion after heating
Graphical models (temperature vs. energy added) also support claims:
- Steeper slope → larger temperature change for the same energy
- Shallower slope → smaller temperature change
Example
Two samples of the same substance have different masses. Both receive the same amount of thermal energy. Which sample experiences a greater temperature increase? Explain your reasoning.
▶️ Answer / Explanation
The smaller mass experiences the greater temperature increase.
The same thermal energy is spread among fewer particles, causing a larger increase in average kinetic energy and therefore temperature.
Example
Equal masses of two different substances receive the same amount of thermal energy. One sample shows a much smaller temperature change. Evaluate a claim explaining why this occurs using particle-level reasoning.
▶️ Answer / Explanation
The substance with the smaller temperature change requires more energy to increase the average kinetic energy of its particles.
At the particle level, the transferred energy is distributed in ways that limit how much particle speed increases, resulting in a smaller temperature rise compared to the other substance.
1.2.A.2 — Calculations in Constant-Pressure Calorimetry
A constant-pressure calorimetry experiment measures the transfer of thermal energy between a reaction (or process) and its surroundings, usually using a coffee-cup calorimeter.
The measured temperature change of a solution is used to calculate the amount of thermal energy absorbed or released.
Key Idea
At constant pressure, the thermal energy change of the solution is related to its:
- Mass of the solution
- Specific heat capacity
- Change in temperature
Calorimetry Equation
The thermal energy gained or lost by a substance is calculated using:
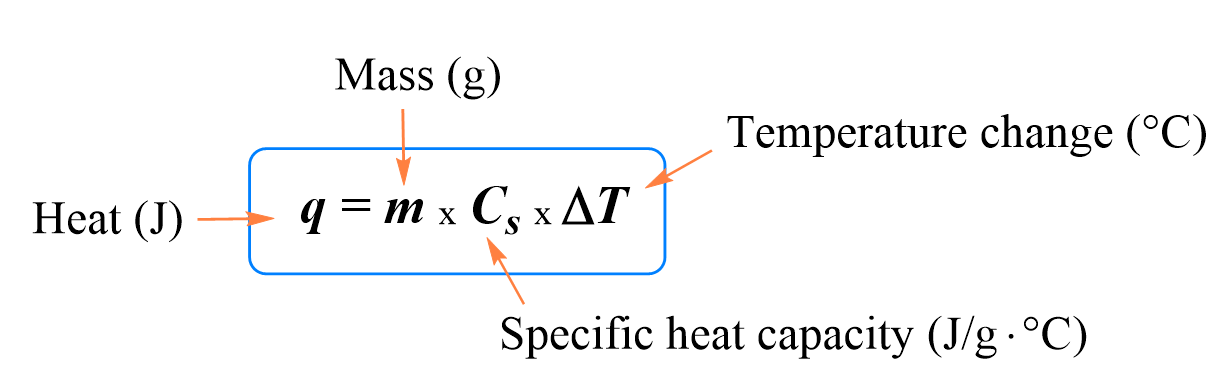
Where:
- \( \mathrm{q} \) = thermal energy (\( \mathrm{J} \))
- \( \mathrm{m} \) = mass (\( \mathrm{g} \))
- \( \mathrm{c} \) = specific heat capacity (\( \mathrm{J\,g^{-1}\,^\circ C^{-1}} \))
- \( \mathrm{\Delta T = T_{final} – T_{initial}} \)
For aqueous solutions, \( \mathrm{c} \) is often assumed to be the same as water:
\( \mathrm{c = 4.18\ J\,g^{-1}\,^\circ C^{-1}} \)
Interpreting the Sign of \( \mathrm{q} \)

- If \( \mathrm{\Delta T > 0} \), then \( \mathrm{q > 0} \): energy is absorbed
- If \( \mathrm{\Delta T < 0} \), then \( \mathrm{q < 0} \): energy is released
In calorimetry:
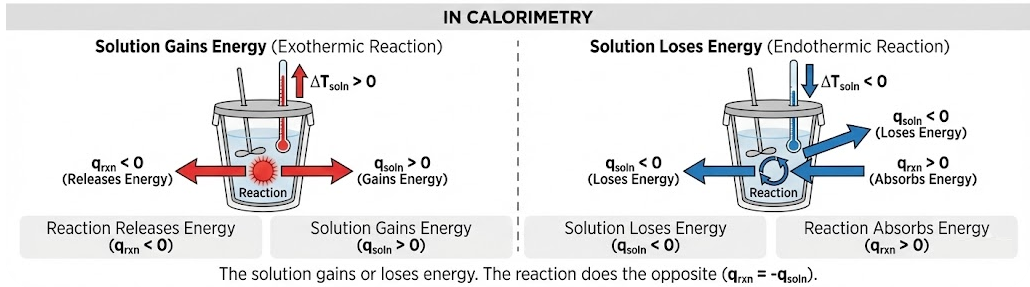
- The solution gains or loses energy
- The reaction does the opposite
Relationship Between Solution and Reaction
At constant pressure:
\( \mathrm{q_{reaction} = – q_{solution}} \)
This relationship allows the energy change of the reaction to be determined from the measured temperature change of the solution.
Steps for Calorimetry Calculations
- Calculate \( \mathrm{\Delta T} \)
- Calculate \( \mathrm{q_{solution}} \) using \( \mathrm{q = mc\Delta T} \)
- Determine \( \mathrm{q_{reaction}} \) using the opposite sign
- Report the result with correct units and precision
Example
In a coffee-cup calorimeter, 100.0 g of water increases in temperature from \( \mathrm{22.5^\circ C} \) to \( \mathrm{27.0^\circ C} \). Calculate the thermal energy absorbed by the solution.
▶️ Answer / Explanation
First, calculate \( \mathrm{\Delta T} \):
\( \mathrm{\Delta T = 27.0 – 22.5 = 4.5^\circ C} \)
Now calculate \( \mathrm{q_{solution}} \):
\( \mathrm{q = 100.0 \times 4.18 \times 4.5} \)
\( \mathrm{q = 1.88 \times 10^{3}\ J} \)
The solution absorbed \( \mathrm{1.88 \times 10^{3}\ J} \) of thermal energy.
Example
During a constant-pressure calorimetry experiment, 75.0 g of solution cools from \( \mathrm{30.0^\circ C} \) to \( \mathrm{24.5^\circ C} \). Calculate the thermal energy change of the reaction. Assume the solution has the specific heat capacity of water.
▶️ Answer / Explanation
Calculate \( \mathrm{\Delta T} \):
\( \mathrm{\Delta T = 24.5 – 30.0 = -5.5^\circ C} \)
Calculate \( \mathrm{q_{solution}} \):
\( \mathrm{q = 75.0 \times 4.18 \times (-5.5)} \)
\( \mathrm{q_{solution} = -1.72 \times 10^{3}\ J} \)
Determine \( \mathrm{q_{reaction}} \):
\( \mathrm{q_{reaction} = +1.72 \times 10^{3}\ J} \)
The reaction absorbed \( \mathrm{1.72 \times 10^{3}\ J} \) of thermal energy.
