1.3B Macroscopic Gas Properties and Kinetic Molecular Theory- Pre AP Chemistry Study Notes - New Syllabus.
1.3B Macroscopic Gas Properties and Kinetic Molecular Theory- Pre AP Chemistry Study Notes
1.3B Macroscopic Gas Properties and Kinetic Molecular Theory- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
1.3.B.1 Explain the relationships between the macroscopic properties of a sample of a gas using the kinetic molecular theory.
1.3.B.2 Create and/or evaluate models that illustrate how a sample of gas responds to changes in macroscopic properties.
Key Concepts:
- 1.3.B The kinetic molecular theory relates the macroscopic properties of a gas to the motion of the particles that comprise the gas. An ideal gas is a gas that conforms to the kinetic molecular theory.
1.3.B.1 — Macroscopic Gas Properties and the Kinetic Molecular Theory
The kinetic molecular theory (KMT) explains the observable (macroscopic) properties of gases by describing the motion and behavior of gas particles. Using KMT, scientists connect particle-level motion to properties such as pressure, volume, temperature, and amount of gas.
Core Assumptions of the Kinetic Molecular Theory
KMT makes the following assumptions about gases:
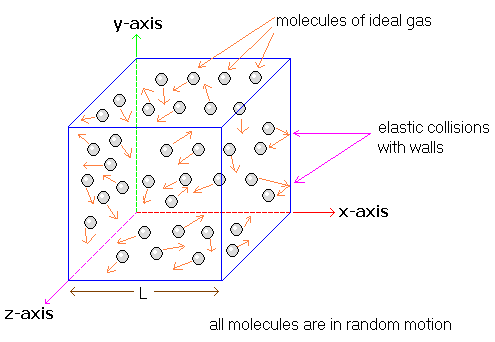
- Gas particles are in constant, random motion
- The volume of individual particles is negligible compared to the container
- There are no significant attractions between gas particles
- Collisions between particles and container walls are elastic
- The average kinetic energy of particles depends only on temperature
Pressure Explained by KMT
According to KMT, gas pressure is caused by collisions of gas particles with the walls of a container.
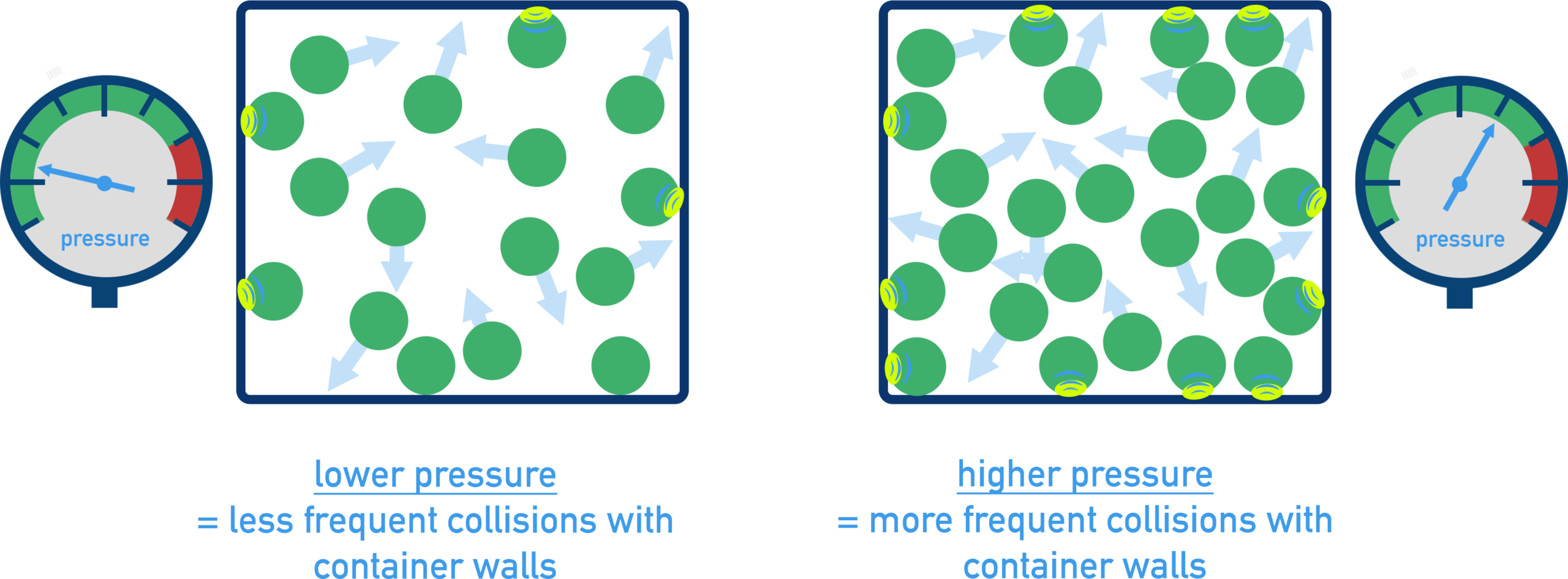
- More frequent collisions → higher pressure
- More forceful collisions → higher pressure
Changes in temperature, volume, or number of particles alter collision behavior and therefore change pressure.
Temperature Explained by KMT
Temperature is a measure of the average kinetic energy of gas particles.
![]()
- Higher temperature → particles move faster
- Lower temperature → particles move slower
Faster-moving particles produce more energetic collisions, affecting pressure and volume.
Volume Explained by KMT
Gas particles spread out to fill the entire volume of their container.
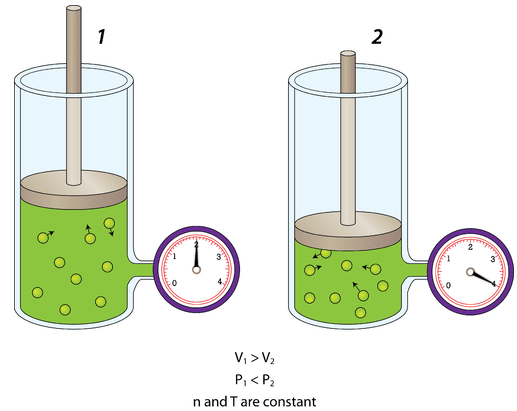
- Larger volume → particles travel farther between collisions
- Smaller volume → particles collide with walls more frequently
Reducing volume at constant temperature increases collision frequency and pressure.
Amount of Gas Explained by KMT
The amount of gas refers to the number of particles present.
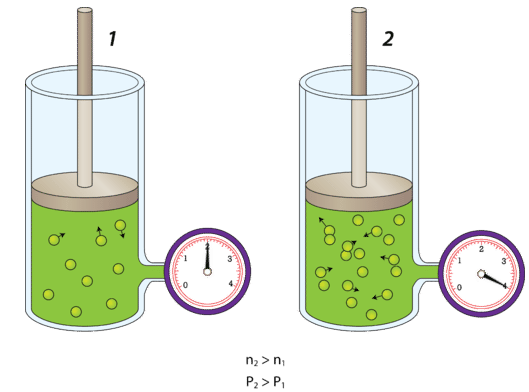
- More particles → more collisions with container walls
- Fewer particles → fewer collisions
At constant temperature and volume, increasing the number of particles increases pressure.
Connecting Macroscopic Properties Using KMT
| Macroscopic Property | Particle-Level Explanation (KMT) |
|---|---|
| Pressure | Collisions of particles with container walls |
| Temperature | Average kinetic energy of particles |
| Volume | Space available for particle motion |
| Amount of gas | Number of particles causing collisions |
Evaluating Models Using KMT
A correct kinetic molecular model must:
- Show random particle motion
- Link changes in motion to temperature
- Explain pressure through collisions
- Relate volume to collision frequency
Models that ignore collisions or particle motion do not accurately represent gas behavior.
Example
Explain why increasing the temperature of a gas in a rigid container increases its pressure, using the kinetic molecular theory.
▶️ Answer / Explanation
Increasing temperature increases the average kinetic energy of gas particles.
Faster-moving particles collide with the container walls more frequently and with greater force, increasing the pressure.
Example
Two gas samples have the same temperature and pressure, but Sample A occupies a larger volume than Sample B. Use the kinetic molecular theory to explain how this is possible.
▶️ Answer / Explanation
If temperature and pressure are the same, the average kinetic energy and collision force are equal.
The larger volume must contain more gas particles, so the increased number of collisions balances the larger container size, resulting in the same pressure.
1.3.B.2 — Gas Responses to Changes in Macroscopic Properties (Models)
Particle (particulate) models are used to show how a sample of gas responds when its macroscopic properties—pressure, volume, temperature, or amount of gas—change. These models are based on the kinetic molecular theory (KMT).
Macroscopic Properties of Gases
The key macroscopic properties that can change in a gas sample are:
- Pressure — force of particle collisions with container walls
- Volume — size of the container
- Temperature — average kinetic energy of particles
- Amount of gas — number of particles
Correct models show how particle motion and collisions change when one of these properties changes.
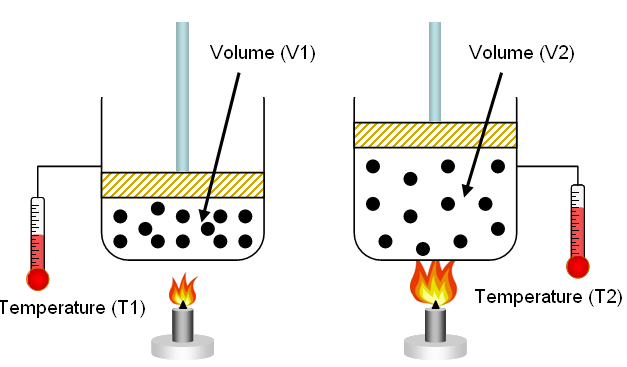
Changing Volume (Constant Temperature and Amount)

When volume decreases:
- Particles are confined to a smaller space
- Collision frequency with container walls increases
- Pressure increases
A correct particle model shows the same number of particles in a smaller container with more frequent wall collisions.
Changing Temperature (Constant Volume and Amount)
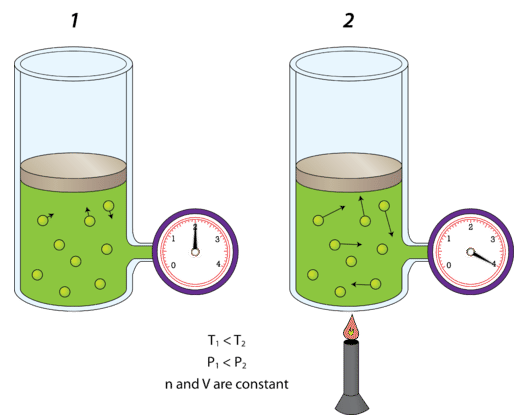
When temperature increases:
- Particles move faster
- Collisions become more forceful
- Pressure increases
A correct model shows longer motion arrows to represent higher particle speed, while particle number and container size remain the same.
Changing Amount of Gas (Constant Volume and Temperature)

When the number of particles increases:
- More particles collide with container walls
- Total force on the walls increases
- Pressure increases
A correct model shows more particles in the same volume, not larger particles.
Changing Pressure (Flexible Containers)
In a flexible container (like a balloon):
- Increasing temperature increases particle speed
- The container expands
- Volume increases while pressure stays balanced
Models should show particles spreading farther apart as volume increases.
Summary of Gas Responses (Particle Models)
| Macroscopic Change | Particle-Level Change | Resulting Effect |
|---|---|---|
| Decreased volume | More frequent wall collisions | Pressure increases |
| Increased temperature | Faster particles, stronger collisions | Pressure increases |
| Increased number of particles | More collisions per second | Pressure increases |
Evaluating the Accuracy of Gas Models
A correct model must:
- Show random particle motion
- Keep particle size constant
- Only change one macroscopic variable at a time
- Clearly connect collisions to pressure
Models that change particle size or stop particle motion are incorrect.
Example
A gas is compressed to half its original volume at constant temperature. Describe how a particle model would change.
▶️ Answer / Explanation
The model would show the same number of particles in a smaller container.
Particles collide with the walls more frequently, explaining the increase in pressure. Particle speed remains unchanged because temperature is constant.
Example
Two particle models represent the same gas sample. Model A shows short motion arrows and Model B shows long motion arrows. The containers are identical in size. Evaluate which model represents the higher temperature and explain the pressure difference.
▶️ Answer / Explanation
Model B represents the higher temperature.
Longer arrows indicate faster particle motion. Faster particles collide with the container walls more forcefully, resulting in greater pressure compared to Model A.
