1.3C Quantitative Gas Relationships- Pre AP Chemistry Study Notes - New Syllabus.
1.3C Quantitative Gas Relationships- Pre AP Chemistry Study Notes
1.3C Quantitative Gas Relationships- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
1.3.C.1 Determine mathematically and/or graphically the quantitative relationship between macroscopic properties of gases.
1.3.C.2 Perform calculations relating to the macroscopic properties of gases.
Key Concepts:
- 1.3.C The relationships between macroscopic properties of a gas, including pressure, temperature, volume, and amount of gas, can be quantified.
1.3.C.1 — Quantitative Relationships Between Macroscopic Properties of Gases
The macroscopic properties of gases—pressure, volume, temperature, and amount of gas—are quantitatively related. These relationships can be determined using mathematical equations and graphical models, and are explained by the kinetic molecular theory.
Key Gas Variables
- Pressure, \( \mathrm{P} \)
- Volume, \( \mathrm{V} \)
- Temperature (in kelvin), \( \mathrm{T} \)
- Amount of gas, \( \mathrm{n} \)
Gas laws describe how these variables change when one or more are held constant.
Pressure–Volume Relationship (Constant Temperature)![]()
When temperature and amount of gas are constant, pressure and volume are inversely proportional.
\( \mathrm{P \propto \dfrac{1}{V}} \)
\( \mathrm{P_1 V_1 = P_2 V_2} \)
As volume decreases, particles collide with the container walls more frequently, so pressure increases.
![]()
Volume–Temperature Relationship (Constant Pressure)![]()
When pressure and amount of gas are constant, volume and temperature are directly proportional.
\( \mathrm{V \propto T} \)
\( \mathrm{\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2}} \)
Temperature must always be measured in kelvin.
![]()
Pressure–Temperature Relationship (Constant Volume)![]()
When volume and amount of gas are constant, pressure and temperature are directly proportional.
\( \mathrm{P \propto T} \)
\( \mathrm{\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}} \)
Higher temperature means faster particle motion and more forceful collisions.
![]()
Graphical Representations of Gas Relationships
| Graph | Shape | Relationship Shown |
|---|---|---|
| Pressure vs. Volume | Curved (hyperbola) | Inverse relationship |
| Volume vs. Temperature | Straight line | Direct relationship |
| Pressure vs. Temperature | Straight line | Direct relationship |
Using Graphs to Determine Relationships
- Straight-line graph → direct proportionality
- Curved graph → inverse proportionality
- Steeper slope → greater rate of change
Quantitative relationships can be extracted by comparing slopes or ratios of values.
Example
A gas occupies \( \mathrm{4.0\ L} \) at \( \mathrm{100\ kPa} \). If the pressure increases to \( \mathrm{200\ kPa} \) at constant temperature, calculate the new volume.
▶️ Answer / Explanation
Use the pressure–volume relationship:
\( \mathrm{P_1 V_1 = P_2 V_2} \)
\( \mathrm{100 \times 4.0 = 200 \times V_2} \)
\( \mathrm{V_2 = 2.0\ L} \)
Example
A graph of volume versus temperature (in kelvin) is a straight line through the origin. Explain what this indicates about the quantitative relationship between volume and temperature, and justify it using particle motion.
▶️ Answer / Explanation
The straight line through the origin indicates a direct proportional relationship between volume and temperature.
As temperature increases, particle speed increases. In a flexible container, faster particles push outward more strongly, causing volume to increase proportionally.
1.3.C.2 — Calculations Involving Macroscopic Properties of Gases
Calculations involving gases use quantitative relationships between the macroscopic properties of a gas: pressure, volume, temperature, and amount of gas. These calculations are based on the gas laws and are consistent with the kinetic molecular theory.
Key Rules for Gas Calculations
- Temperature must always be converted to kelvin (K)
- Units must be consistent throughout the calculation
- Only one variable should change for simple gas-law problems
Common Gas Laws Used in Calculations
| Gas Law | Variables Related | Mathematical Form |
|---|---|---|
| Boyle’s Law | Pressure & Volume | \( \mathrm{P_1V_1 = P_2V_2} \) |
| Charles’s Law | Volume & Temperature | \( \mathrm{\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2}} \) |
| Gay-Lussac’s Law | Pressure & Temperature | \( \mathrm{\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}} \) |
| Combined Gas Law | P, V, & T | \( \mathrm{\dfrac{P_1V_1}{T_1} = \dfrac{P_2V_2}{T_2}} \) |
| Ideal Gas Law | P, V, T, & n | \( \mathrm{PV = nRT} \) |
The Ideal Gas Law
The ideal gas law relates all four macroscopic gas properties: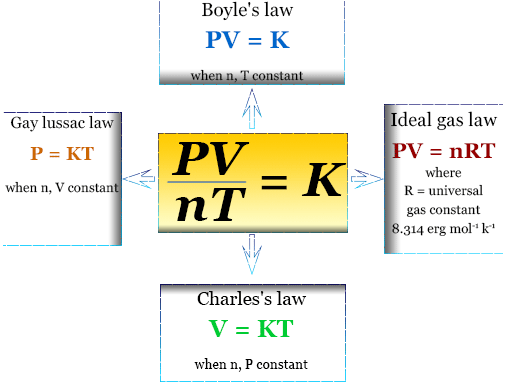
\( \mathrm{PV = nRT} \)
- \( \mathrm{P} \) = pressure
- \( \mathrm{V} \) = volume
- \( \mathrm{n} \) = amount of gas (mol)
- \( \mathrm{T} \) = temperature (K)
- \( \mathrm{R} \) = gas constant
The value of \( \mathrm{R} \) depends on the pressure units used.
Steps for Solving Gas-Law Problems
- Write down the given quantities and the unknown
- Convert temperature to kelvin
- Select the appropriate gas law
- Substitute values with units
- Solve and report with correct units and precision
Common Relationships to Remember
| Change | Result (Constant Other Variables) |
|---|---|
| Volume ↓ | Pressure ↑ |
| Temperature ↑ | Pressure ↑ or Volume ↑ |
| Amount of gas ↑ | Pressure ↑ |
Example
A gas occupies \( \mathrm{3.0\ L} \) at \( \mathrm{150\ kPa} \). What volume will it occupy at \( \mathrm{75\ kPa} \) if temperature remains constant?
▶️ Answer / Explanation
Use Boyle’s law:
\( \mathrm{P_1V_1 = P_2V_2} \)
\( \mathrm{150 \times 3.0 = 75 \times V_2} \)
\( \mathrm{V_2 = 6.0\ L} \)
Example
A sample of gas has a volume of \( \mathrm{2.50\ L} \) at \( \mathrm{101\ kPa} \) and \( \mathrm{27^\circ C} \). Calculate the new pressure if the volume is compressed to \( \mathrm{1.75\ L} \) and the temperature increases to \( \mathrm{57^\circ C} \).
▶️ Answer / Explanation
Convert temperatures to kelvin:
\( \mathrm{T_1 = 300\ K,\ \ T_2 = 330\ K} \)
Use the combined gas law:
\( \mathrm{\dfrac{P_1V_1}{T_1} = \dfrac{P_2V_2}{T_2}} \)
\( \mathrm{\dfrac{101 \times 2.50}{300} = \dfrac{P_2 \times 1.75}{330}} \)
\( \mathrm{P_2 = 157\ kPa} \)
