4.1C Molarity and Solution Concentration- Pre AP Chemistry Study Notes - New Syllabus.
4.1C Molarity and Solution Concentration- Pre AP Chemistry Study Notes
4.1C Molarity and Solution Concentration- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
4.1.C.1 Create and/or evaluate models that represent the concentration of a solution.
4.1.C.2 Perform calculations relating to the molarity of solutions.
Key Concepts:
- 4.1.C Molarity is one way to quantify the concentration of a solution. It describes the number of dissolved particles in a unit volume of that solution.
4.1.C.1 — Modeling the Concentration of a Solution (Molarity)
The concentration of a solution describes how much solute is dissolved in a given amount of solvent or solution. One common way to quantify concentration is molarity, which connects measurable quantities to a particle-level model.
According to this standard, concentration models must clearly represent the number of dissolved particles relative to the volume of solution.
Definition of Molarity
Molarity (\( \mathrm{M} \)) is defined as the number of moles of solute per liter of solution:
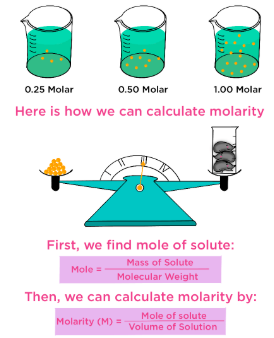
\( \mathrm{M = \dfrac{n}{V}} \)
- \( \mathrm{n} \) = moles of solute
- \( \mathrm{V} \) = volume of solution in \( \mathrm{L} \)
Molarity directly reflects how many dissolved particles are present in a fixed volume.
Particle-Level Meaning of Concentration
At the particle level:
- Higher molarity → more dissolved particles per unit volume
- Lower molarity → fewer dissolved particles per unit volume
Changing concentration changes the spacing of particles, not the type of particles present.
Modeling Concentration Using Particle Diagrams
In a correct particulate model:
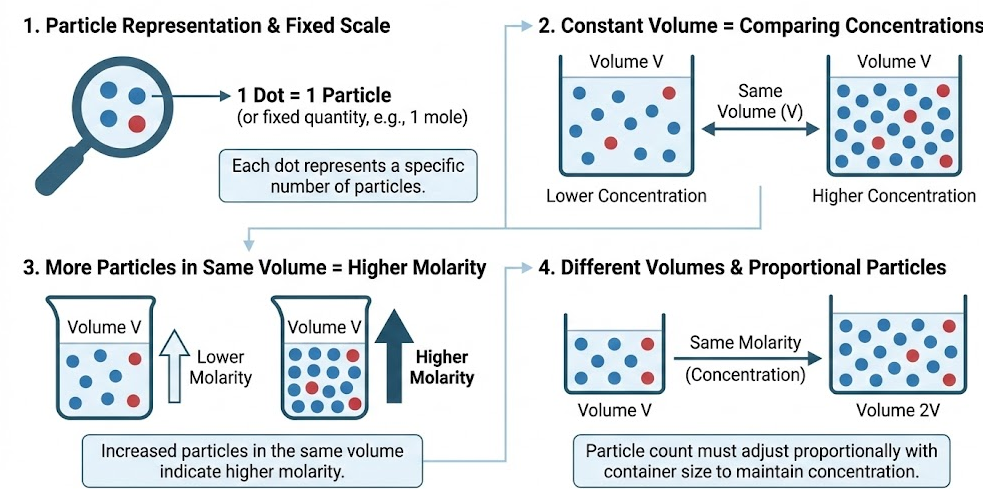
- Each dot or ion represents a fixed number of particles
- The container volume is kept constant when comparing concentrations
- More particles in the same volume indicate higher molarity
A model showing different container sizes must adjust particle count accordingly.
Dilute vs Concentrated Solutions
Dilute and concentrated are relative terms:
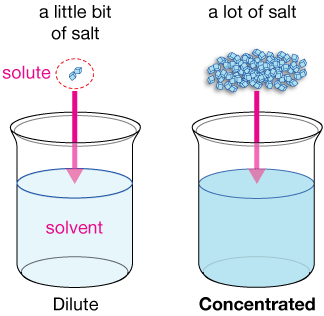
- Dilute → low molarity, fewer particles per unit volume
- Concentrated → high molarity, more particles per unit volume
These terms are qualitative and must be supported by particle models or numerical data.
Macroscopic Interpretation of Concentration
Changes in concentration affect observable properties such as:
- Color intensity (for colored solutions)
- Electrical conductivity (for ionic solutions)
- Reaction rate when concentration is a variable
These changes occur because particle collision frequency changes with concentration.
Evaluating Models of Solution Concentration
To evaluate a concentration model, check that it:
- Clearly represents particle count
- Uses consistent volume when comparing concentrations
- Accurately reflects changes in molarity
Models that change container size without explanation can be misleading.
Comparing Concentration Models
| Model Feature | Low Molarity | High Molarity |
|---|---|---|
| Particle count | Few particles | Many particles |
| Particle spacing | Large spacing | Small spacing |
| Collision frequency | Low | High |
Creating and Evaluating Claims
A strong claim about solution concentration must:
- Reference molarity or particle count
- Link particle-level models to volume
- Be consistent with quantitative or visual data
Claims based only on appearance without particle reasoning are incomplete.
Example
Two beakers contain equal volumes of solution. Beaker A shows twice as many dissolved particles as Beaker B. Compare the molarities of the two solutions.
▶️ Answer / Explanation
Beaker A has a higher molarity than Beaker B.
Because both solutions have the same volume, the solution with more dissolved particles has a greater number of moles per liter.
Example
Two particulate models show the same number of dissolved particles, but one container has twice the volume of the other. Determine which solution has the greater molarity and justify your answer.
▶️ Answer / Explanation
The solution with the smaller volume has the greater molarity.
Molarity depends on the number of particles per unit volume. With the same number of particles, increasing the volume decreases the molarity.
4.1.C.2 — Calculations Involving the Molarity of Solutions
Molarity calculations quantitatively relate the amount of dissolved particles (in moles) to the volume of solution. These calculations connect symbolic equations, numerical data, and particle-level understanding.
Accurate molarity calculations require correct units, proper rearrangement of formulas, and attention to experimental context.
Fundamental Molarity Equation
Molarity is defined as:
\( \mathrm{M = \dfrac{n}{V}} \)
- \( \mathrm{M} \) = molarity (\( \mathrm{mol\,L^{-1}} \))
- \( \mathrm{n} \) = moles of solute (\( \mathrm{mol} \))
- \( \mathrm{V} \) = volume of solution in liters (\( \mathrm{L} \))
Volume must always be in liters before substitution.
Rearranging the Molarity Equation
The molarity equation can be rearranged depending on the unknown quantity:
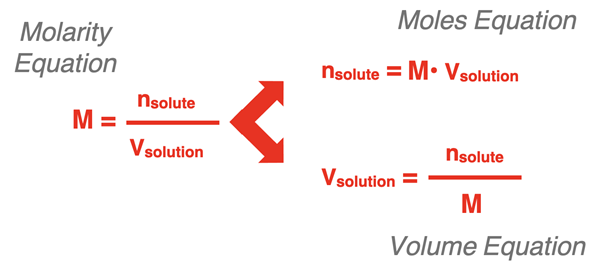
Correct rearrangement ensures dimensional consistency and valid results.
Calculating Moles from Mass (When Needed)
If mass is given instead of moles, convert mass to moles first:
\( \mathrm{n = \dfrac{m}{M_r}} \)
- \( \mathrm{m} \) = mass of solute (\( \mathrm{g} \))
- \( \mathrm{M_r} \) = molar mass (\( \mathrm{g\,mol^{-1}} \))
This step is essential before using the molarity equation.
Dilution Calculations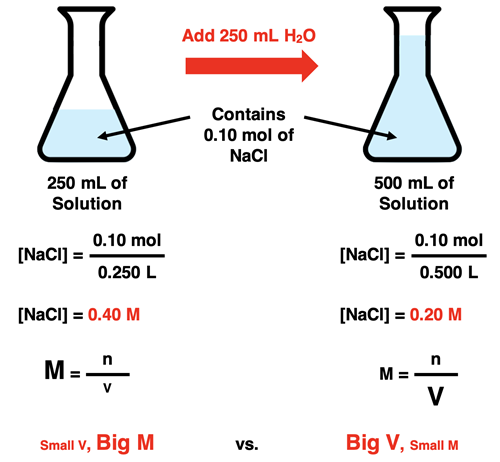
During dilution, the number of moles of solute remains constant.
This relationship is described by:
\( \mathrm{M_1V_1 = M_2V_2} \)
- Subscript 1 = before dilution
- Subscript 2 = after dilution
Dilution decreases molarity by increasing volume without changing particle count.
Common Calculation Mistakes
- Using milliliters instead of liters
- Forgetting to convert mass to moles
- Applying the dilution equation when no dilution occurs
Each step must be checked for correct units and logical consistency.
Evaluating Quantitative Claims
When evaluating a molarity calculation, verify that:
- The correct equation is chosen
- Units are converted properly
- The numerical result matches the physical situation
Numerical answers without unit analysis are incomplete.
Example
Calculate the molarity of a solution prepared by dissolving \( \mathrm{0.50\ mol} \) of sodium chloride in \( \mathrm{2.0\ L} \) of solution.
▶️ Answer / Explanation
Use the molarity equation:
\( \mathrm{M = \dfrac{n}{V}} \)
Substitute the given values:
\( \mathrm{M = \dfrac{0.50}{2.0} = 0.25\ M} \)
The solution has a molarity of \( \mathrm{0.25\ M} \).
Example
A student prepares \( \mathrm{250\ mL} \) of a \( \mathrm{0.80\ M} \) potassium nitrate solution. Determine the number of moles of solute present.
▶️ Answer / Explanation
First convert volume to liters:
\( \mathrm{250\ mL = 0.250\ L} \)
Rearrange the molarity equation:
\( \mathrm{n = M \times V} \)
Substitute values:
\( \mathrm{n = 0.80 \times 0.250 = 0.20\ mol} \)
The solution contains \( \mathrm{0.20\ mol} \) of potassium nitrate.
