4.3B pH and Hydrogen Ion Concentration- Pre AP Chemistry Study Notes - New Syllabus.
4.3B pH and Hydrogen Ion Concentration- Pre AP Chemistry Study Notes
4.3B pH and Hydrogen Ion Concentration- Pre AP Chemistry Study Notes – New Syllabus.
LEARNING OBJECTIVE
4.3.B.1 Explain the relationship between the hydrogen concentration and the pH of a solution.
4.3.B.2 Calculate the pH of a solution.
Key Concepts:
- 4.3.B The pH of a solution is a measure of the molarity of H₃O⁺ (or H⁺) in the solution.
4.3.B.1 — Relationship Between Hydrogen Ion Concentration and pH
The pH of a solution is a numerical scale used to describe the hydrogen ion concentration, \( \mathrm{[H^+]} \), in aqueous solutions. Because hydrogen ion concentrations can vary over a very wide range, pH uses a logarithmic scale to make comparisons easier.
Definition of pH
The pH of a solution is defined mathematically as:
\( \mathrm{pH = -\log[H^+]} \)
This equation shows that pH depends directly on the hydrogen ion concentration.
![]()
Logarithmic Nature of the pH Scale
The pH scale is logarithmic, meaning:
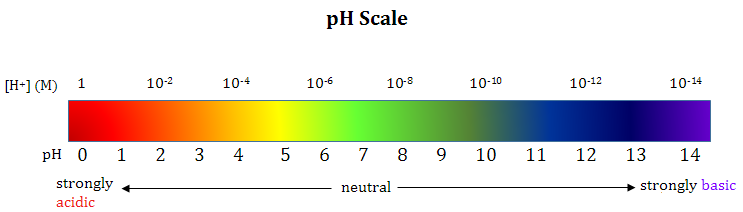
- A change of 1 pH unit represents a tenfold change in \( \mathrm{[H^+]} \)
- A decrease of 1 pH unit means \( \mathrm{[H^+]} \) increases by a factor of 10
- An increase of 1 pH unit means \( \mathrm{[H^+]} \) decreases by a factor of 10
Therefore, small numerical changes in pH correspond to large changes in hydrogen ion concentration.
Inverse Relationship Between pH and \( \mathrm{[H^+]} \)
pH and hydrogen ion concentration are inversely related:
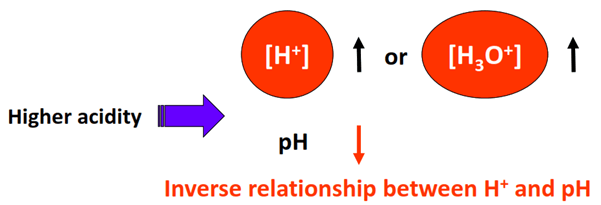
- As \( \mathrm{[H^+]} \) increases, pH decreases
- As \( \mathrm{[H^+]} \) decreases, pH increases
More acidic solutions have higher hydrogen ion concentrations and lower pH values.
Acidic, Neutral, and Basic Solutions
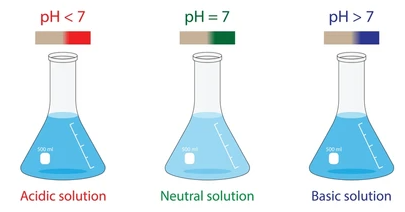
- Acidic: \( \mathrm{pH < 7} \), high \( \mathrm{[H^+]} \)
- Neutral: \( \mathrm{pH = 7} \), \( \mathrm{[H^+] = 1.0 \times 10^{-7}\,M} \)
- Basic: \( \mathrm{pH > 7} \), low \( \mathrm{[H^+]} \)
Neutral water has equal concentrations of \( \mathrm{H^+} \) and \( \mathrm{OH^-} \).
Comparing Hydrogen Ion Concentrations
Using the logarithmic relationship:
- A solution with pH 3 has 10 times more \( \mathrm{H^+} \) than pH 4
- A solution with pH 3 has 100 times more \( \mathrm{H^+} \) than pH 5
This explains why lower-pH acids are much more reactive and corrosive.
Using pH to Evaluate Acid Strength (Conceptually)
At the same concentration:
- Strong acids produce higher \( \mathrm{[H^+]} \)
- Weak acids produce lower \( \mathrm{[H^+]} \)
- Lower pH indicates greater ionization
However, pH alone does not define acid strength unless concentrations are equal.
Evaluating Claims About pH and \( \mathrm{[H^+]} \)
A complete explanation must:
- Reference hydrogen ion concentration
- Use the logarithmic nature of the pH scale
- Explain the inverse relationship between pH and \( \mathrm{[H^+]} \)
Claims that say “lower pH means stronger acid” without discussing \( \mathrm{[H^+]} \) are incomplete.
Example
Compare the hydrogen ion concentrations of two solutions: one with pH 4 and one with pH 6.
▶️ Answer / Explanation
The pH 4 solution has a lower pH and therefore a higher hydrogen ion concentration.
Because the pH difference is 2 units, the pH 4 solution has \( \mathrm{10^2 = 100} \) times more \( \mathrm{H^+} \) than the pH 6 solution.
Example
A solution’s hydrogen ion concentration increases by a factor of 100. Explain how the pH of the solution changes.
▶️ Answer / Explanation
An increase in \( \mathrm{[H^+]} \) by a factor of 100 corresponds to a decrease in pH of 2 units.
This is because the pH scale is logarithmic, and each pH unit represents a tenfold change in hydrogen ion concentration.
4.3.B.2 — Calculating the pH of a Solution
The pH of a solution can be calculated quantitatively from its hydrogen ion concentration, \( \mathrm{[H^+]} \). Because pH is a logarithmic measure, even small numerical changes in pH represent large changes in acidity.
pH Equation
The mathematical relationship between pH and hydrogen ion concentration is:
\( \mathrm{pH = -\log[H^+]} \)
This equation is used whenever \( \mathrm{[H^+]} \) is known.
Key Rules Before Calculating pH
- \( \mathrm{[H^+]} \) must be in moles per liter (M)
- Only the base-10 logarithm is used
- The negative sign must be included
Forgetting the negative sign is a common error.
Calculating pH: Step-by-Step Method
- Identify the hydrogen ion concentration \( \mathrm{[H^+]} \)
- Substitute the value into the pH equation
- Evaluate the logarithm
- Apply the negative sign
Interpreting the Calculated pH
- \( \mathrm{pH < 7} \) → acidic solution
- \( \mathrm{pH = 7} \) → neutral solution
- \( \mathrm{pH > 7} \) → basic solution
The calculated pH must always be interpreted alongside hydrogen ion concentration.
Estimating pH Without a Calculator
When \( \mathrm{[H^+]} \) is written in scientific notation:
- If \( \mathrm{[H^+] = 1.0 \times 10^{-x}} \), then \( \mathrm{pH = x} \)
This is useful for strong acids and Pre-AP estimation problems.
Strong Acids and pH Calculations
For strong monoprotic acids:
- Each acid molecule produces one \( \mathrm{H^+} \)
- \( \mathrm{[H^+]} \) equals the acid concentration
This allows direct pH calculation from molarity.
Common Errors to Avoid
- Forgetting the negative sign
- Using pH = log[H⁺]
- Confusing pH value with hydrogen ion concentration
Example
Calculate the pH of a solution with a hydrogen ion concentration of \( \mathrm{1.0 \times 10^{-3}\ M} \).
▶️ Answer / Explanation
Step 1: Write the pH equation:
\( \mathrm{pH = -\log[H^+]} \)
Step 2: Substitute the value:
\( \mathrm{pH = -\log(1.0 \times 10^{-3})} \)
Step 3: Evaluate:
\( \mathrm{pH = 3.0} \)
The solution is acidic.
Example
A solution has a hydrogen ion concentration of \( \mathrm{3.2 \times 10^{-5}\ M} \). Calculate the pH.
▶️ Answer / Explanation
Step 1: Use the pH equation:
\( \mathrm{pH = -\log(3.2 \times 10^{-5})} \)
Step 2: Evaluate:
\( \mathrm{pH \approx 4.49} \)
The solution is acidic.
