Pre AP Chemistry -3.2B Stoichiometry and Quantitative Relationships- MCQ Exam Style Questions -New Syllabus 2025-2026
Pre AP Chemistry -3.2B Stoichiometry and Quantitative Relationships- MCQ Exam Style Questions – New Syllabus 2025-2026
Pre AP Chemistry -3.2B Stoichiometry and Quantitative Relationships- MCQ Exam Style Questions – Pre AP Chemistry – per latest Pre AP Chemistry Syllabus.
Calcium phosphate forms when calcium chloride and sodium phosphate solutions react together.
\(x CaCl_2 + y Na_3PO_4 → 2Ca_3(PO_4)_2 + 12NaCl\)
Which values of x and y balance the equation?
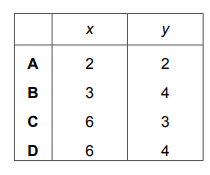
▶️ Answer/Explanation
Ans: D
To balance the equation \(x CaCl_2 + y Na_3PO_4 → 2Ca_3(PO_4)_2 + 12NaCl\):
- Calcium (Ca): On the right, there are \(2 \times 3 = 6\) Ca atoms. Thus, \(x = 6\) to balance Ca.
- Phosphate (PO₄): On the right, there are \(2 \times 2 = 4\) PO₄ groups. Thus, \(y = 4\) to balance PO₄.
- Chlorine (Cl) & Sodium (Na): With \(x = 6\) and \(y = 4\), Cl balances as \(6 \times 2 = 12\) on the left (matching 12 NaCl), and Na balances as \(4 \times 3 = 12\) on the left (matching 12 NaCl).
Thus, the correct values are \(x = 6\) and \(y = 4\).
Iron(III) oxide is reduced by carbon monoxide to produce iron and carbon dioxide. What is the balanced equation for this reaction?
A) \(Fe_2O_3 + 2CO → 2Fe + 2CO_2\)
B) \(Fe_2O_3 + 3CO → 2Fe + 3CO_2\)
C) \(2Fe_2O_3 + 6CO → 2Fe + 6CO_2\)
D) \(2Fe_2O_3 + 3CO → 4Fe + 3CO_2\)
▶️ Answer/Explanation
Ans: B
The balanced equation for the reduction of iron(III) oxide (\(Fe_2O_3\)) by carbon monoxide (\(CO\)) is:
1. Iron atoms: \(Fe_2O_3\) contains 2 Fe, so 2 Fe must appear on the product side.
2. Oxygen atoms: \(Fe_2O_3\) has 3 O, which forms 3 \(CO_2\) molecules (balancing O atoms).
3. Carbon atoms: 3 \(CO\) molecules are needed to provide 3 C atoms for \(3CO_2\).
Thus, the correct balanced equation is \(Fe_2O_3 + 3CO → 2Fe + 3CO_2\).
What is the balanced equation for the reaction between magnesium and dilute sulfuric acid?
A) Mg + \(H_2SO_4\) → \(MgSO_4\) + \(H_2\)
B) Mg + \(2H_2SO_4\) → \(Mg(SO_4)_2\) + \(2H_2\)
C) 2Mg + \(H_2SO_4\) → \(Mg_2SO_4\) + \(H_2\)
D) 2Mg + \(3H_2SO_4\) → \(Mg_2(SO_4)_3\) + \(3H_2\)
▶️ Answer/Explanation
Ans: A
Magnesium (Mg) reacts with dilute sulfuric acid (\(H_2SO_4\)) to form magnesium sulfate (\(MgSO_4\)) and hydrogen gas (\(H_2\)). The reaction is a single displacement where Mg replaces hydrogen in \(H_2SO_4\). The balanced equation is:
\[ \text{Mg} + H_2SO_4 \rightarrow MgSO_4 + H_2 \]
Option A is correct because it is already balanced with 1 Mg, 2 H, 1 S, and 4 O atoms on both sides. The other options either incorrectly modify the products or are unbalanced.
Methane burns in oxygen to produce carbon dioxide and water.
What is the balanced equation for this reaction?
A \(CH_4 + 2O_2 \rightarrow 2CO_2 + 2H_2O\)
B \(CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O\)
C \(CH_4 + 2O_2 \rightarrow CO_2 + H_2O\)
D \(CH_4 + O_2 \rightarrow CO_2 + 2H_2O\)
▶️ Answer/Explanation
Ans: B
The unbalanced equation is \(CH_4 + O_2 \rightarrow CO_2 + H_2O\).
First, balance the hydrogen atoms by placing a 2 in front of \(H_2O\): \(CH_4 + O_2 \rightarrow CO_2 + 2H_2O\).
Next, balance the oxygen atoms by placing a 2 in front of \(O_2\): \(CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O\).
Now, the equation is balanced with 1 C, 4 H, and 4 O atoms on both sides.
What is the balanced chemical equation for the reaction between calcium and water?
A \(Ca + H_2O \rightarrow CaOH + H_2\)
B \(Ca + H_2O \rightarrow Ca(OH)_2 + H_2\)
C \(Ca + 2H_2O \rightarrow CaOH + H_2\)
D \(Ca + 2H_2O \rightarrow Ca(OH)_2 + H_2\)
▶️ Answer/Explanation
Ans: D
Calcium reacts with water to form calcium hydroxide (\(Ca(OH)_2\)) and hydrogen gas (\(H_2\)). The unbalanced equation is:
\[ Ca + H_2O \rightarrow Ca(OH)_2 + H_2 \]
To balance the hydrogens, we need 2 water molecules, resulting in:
\[ Ca + 2H_2O \rightarrow Ca(OH)_2 + H_2 \]
This ensures equal numbers of each atom on both sides.
The equation for the reaction between magnesium and dilute hydrochloric acid is shown.
\(Mg + 2HCl → MgCl_2 + H_2\)
Which mass of magnesium chloride is formed when 48.0 g of magnesium completely reacts with excess dilute hydrochloric acid?
A) 23.8 g
B) 47.5 g
C) 95.0 g
D) 190 g
▶️ Answer/Explanation
Ans: D
Step 1: Calculate moles of magnesium (Mg)
Molar mass of \(Mg = 24.3 \, \text{g/mol}\)
Moles of \(Mg = \frac{48.0 \, \text{g}}{24.3 \, \text{g/mol}} = 1.975 \, \text{mol}\)
Step 2: Determine moles of magnesium chloride (\(MgCl_2\)) formed
From the balanced equation, \(1 \, \text{mol} \, Mg\) produces \(1 \, \text{mol} \, MgCl_2\).
Thus, \(1.975 \, \text{mol} \, Mg\) produces \(1.975 \, \text{mol} \, MgCl_2\).
Step 3: Calculate mass of \(MgCl_2\)
Molar mass of \(MgCl_2 = 24.3 + 2 \times 35.5 = 95.3 \, \text{g/mol}\)
Mass of \(MgCl_2 = 1.975 \, \text{mol} \times 95.3 \, \text{g/mol} = 188.2 \, \text{g}\)
Rounding to 3 significant figures, the closest option is 190 g (D).
The equation for the reaction between magnesium and dilute sulfuric acid is shown.
\(Mg + H_2SO_4 → MgSO_4 + H_2\)
Mr of \(MgSO_4\) is 120
Which mass of magnesium sulfate will be formed if 12 g of magnesium are reacted with sulfuric acid?
A 5g B 10g C 60g D 120g
▶️ Answer/Explanation
Ans: C
1. Moles of Mg: Given mass = 12 g, Molar mass of Mg = 24 g/mol
\[ \text{Moles of Mg} = \frac{12}{24} = 0.5 \text{ mol} \]
2. Reaction stoichiometry: 1 mol Mg produces 1 mol \(MgSO_4\)
\[ \text{Moles of } MgSO_4 = 0.5 \text{ mol} \]
3. Mass of \(MgSO_4\): Molar mass = 120 g/mol
\[ \text{Mass} = 0.5 \times 120 = 60 \text{ g} \]
Thus, the correct answer is C (60g).
The incomplete equation for photosynthesis is shown.
![]()
Compound P is a product of the reaction. Which row describes the values of w, x and y and gives the empirical formula of compound P?

▶️ Answer/Explanation
Ans: A
The balanced equation for photosynthesis is:
\[ 6CO_2 + 6H_2O \rightarrow C_6H_{12}O_6 + 6O_2 \]
Here, \( w = 6 \), \( x = 6 \), and \( y = 6 \). The empirical formula of glucose (\( C_6H_{12}O_6 \)) simplifies to \( CH_2O \). Thus, the correct row is:
w = 6, x = 6, y = 6, Empirical formula of P = CH2O (Option A).
Propane burns in oxygen.
\(C_{3}H_{8}+xO_{2}\rightarrow 3CO_{2}+yH_{2}O\)
Which values of x and y balance the equation?
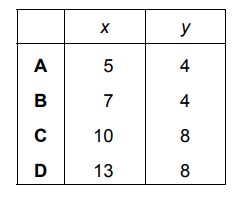
▶️ Answer/Explanation
Ans: A
To balance the equation \(C_{3}H_{8} + xO_{2} \rightarrow 3CO_{2} + yH_{2}O\):
- Carbon is already balanced (3 on both sides).
- Hydrogen: Left side has 8 H, so \(y = 4\) to balance (since \(H_{2}O\) has 2 H per molecule).
- Oxygen: Right side has \(3 \times 2 + 4 \times 1 = 10\) O atoms, so \(x = 5\) (since \(O_{2}\) provides 2 O per molecule).
Thus, the balanced equation is \(C_{3}H_{8} + 5O_{2} \rightarrow 3CO_{2} + 4H_{2}O\), meaning \(x = 5\) and \(y = 4\).
Aluminium reacts with fluorine.
\[ xAl(s) + yF_2(g) \rightarrow zAlF_3(s) \]
Which values of x, y and z balance the equation?
| x | y | z | |
| A B C D | 1 2 3 4 | 2 3 2 3 | 1 2 3 4 |
▶️ Answer/Explanation
Ans: B
To balance the equation:
1. Aluminium (Al): Ensure the number of Al atoms is equal on both sides. If \( z = 2 \), then \( x = 2 \).
2. Fluorine (F): Since \( F_2 \) is diatomic, \( y = 3 \) ensures \( 6F \) atoms, matching \( 2AlF_3 \) (which also requires \( 6F \)).
Thus, the balanced equation is:
\[ 2Al(s) + 3F_2(g) \rightarrow 2AlF_3(s) \]
This corresponds to Option B (\( x = 2 \), \( y = 3 \), \( z = 2 \)).
\(25\,cm^3\) of \(0.1\,mol/dm^3\) hydrochloric acid exactly neutralises \(20\,cm^3\) of aqueous sodium hydroxide. The equation for this reaction is:
\[ NaOH + HCl \rightarrow NaCl + H_2O \]
What is the concentration of the sodium hydroxide solution?
A) \(0.080\,mol/dm^3\)
B) \(0.800\,mol/dm^3\)
C) \(0.125\,mol/dm^3\)
D) \(1.25\,mol/dm^3\)
▶️ Answer/Explanation
Ans: C (\(0.125\,mol/dm^3\))
Step 1: Write the balanced equation
\[ NaOH + HCl \rightarrow NaCl + H_2O \]
The reaction shows a 1:1 molar ratio between NaOH and HCl.
Step 2: Calculate moles of HCl used
\[ \text{Moles of HCl} = \text{Concentration} \times \text{Volume (in dm}^3\text{)} = 0.1 \times \frac{25}{1000} = 0.0025\,mol \]
Step 3: Determine moles of NaOH neutralised
Since the ratio is 1:1, moles of NaOH = moles of HCl = \(0.0025\,mol\).
Step 4: Calculate concentration of NaOH
\[ \text{Concentration of NaOH} = \frac{\text{Moles}}{\text{Volume (in dm}^3\text{)}} = \frac{0.0025}{\frac{20}{1000}} = 0.125\,mol/dm^3 \]
