Question
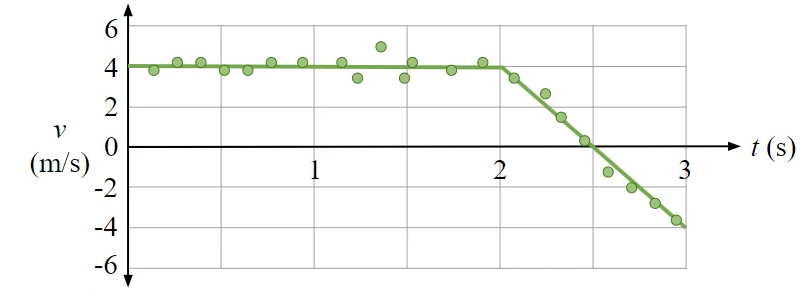
The horizontal velocity of a student moving in a hallway is shown in the graph above. At \(t=0\), the student is at \(x=+3.5 \mathrm{~m}\).
(a) Determine the position of the student at \(t=3 \mathrm{~s}\).
(b) What is the most positive position the student reaches?
(c) Determine the average velocity of the student between \(t=0\) and \(t=3 \mathrm{~s}\) .
(d) Determine the average speed of the student between \(t=0\) and \(t=3 \mathrm{~s}\)
(e) Determine the average acceleration of the student between \(2 \mathrm{~s}\) and \(2.5 \mathrm{~s}\)
(f) Determine the average acceleration of the student between \(2.5 \mathrm{~s}\) and \(3.0 \mathrm{~s}\)
▶️Answer/Explanation
Ans:
a.
\( \begin{gathered}v=\frac{dx}{d t} \\ \int v_{d t}=\int d x \\ \int v_{d t}= Area~ under~ (v-t) ~graph
\\ \Rightarrow \quad 2 \times 4+\frac{1}{2} 0.5 \times 4+\frac{1}{2} \frac{1}{2}(-4) \\ x_f-x_i=8+1-1\\x_f=8+3.5=11.5 m\end{gathered} \)
b.
student is moving in one direction up to 2.5 second,
So maximum positive position will be $x_f-3.5=2 \times 4+\frac{1}{2} 0.5 \times 4\Rightarrow x_f=12.5 m $
c.
\( \begin{aligned}\langle v\rangle & =\frac{\Delta x}{\Delta t} \\ \Delta x & =\text { Area } \\ & =\frac{8+1-1}{3} \\ & =2.67 \mathrm{~m} / \mathrm{s}\end{aligned} \)
d.
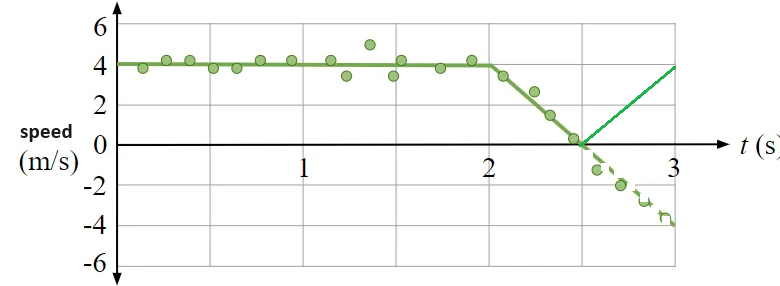
average speed is total speed (modulus of displacement) / total time taken
if we draw speed time graph and then calculate the area we will get the distance covered
\(\begin{aligned}
\langle\bar{v}\rangle & =\frac{8+1+1}{3} \\
& =3.33 \mathrm{m/s}
\end{aligned}\)
e .
\( \begin{aligned}\langle a\rangle & =\frac{v_f-v_i}{t_f-t_i} \\ & =\frac{0-4}{2.5-2} \\ & =-8 \mathrm{~m} / \mathrm{s}^2\end{aligned} \)
f.
\( \begin{aligned}\langle a\rangle & =\frac{v_f-v_i}{t_f-t_i} \\ & =\frac{-4-0}{3-2.5} \\ & =-8 \mathrm{~m} / \mathrm{s}^2\end{aligned} \)
Question
▶️Answer/Explanation
Ans:
a.
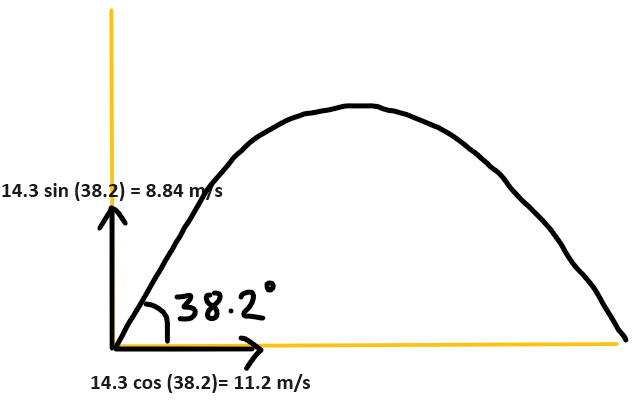
\( \begin{gathered}x=\left(u_0\right)_x t+\frac{1}{2} a_x t^2 \\ 22.52=11.2 t+0 \\ t=2.0~ \mathrm{sec}\end{gathered} \)
\( \begin{aligned} y_{-} y_0 & =\left(u_0\right)_y t+\frac{1}{5} a_y t^2 \\ 0-y_0 & =8.24(2)+\frac{1}{5}(-9.8)(2)^2 \\ y_0 & =1.92 \mathrm{~m}\end{aligned} \)
b(i).
\(\begin{aligned} & V_y^2=V_{y_0}{ }^2+2 a_y\left(y-y_0\right) \\ & V_y^2=(8.84)^2+2(-9.8)(-1.92) \\ & \sqrt{V_y^2}=\sqrt{115.7776} \\ & V_y=10.76 \mathrm{~m} / \mathrm{s}\end{aligned}\)
b(ii).
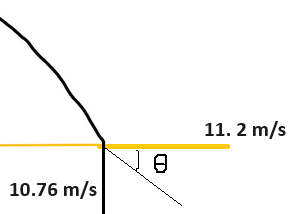
\( \begin{aligned} \tan \theta & =\frac{10.76}{11.2} \\ \theta & =\tan ^{-1}(0.96) \\ \theta & =43.8^{\circ}\end{aligned} \)
c.
Maximum height will be at half of time of flight of its motion
\(\begin{aligned} & y=y_0+v_{y_0} t+\frac{1}{2} a_x t^2 \\ & y=1.92+8.84 t+\frac{1}{2}(-9.8) t^2 \\ & y=-4.9 t^2+8.84 t+1.92 \\ & y=-4.9(1)^2+8.84(1)+1.92 \\ & y=5.86 \text { meters }\end{aligned}\)
d. At max. height vertical component of velocity will be zero , only horizontal will be present so , speed $=11.2 m/s$
Question
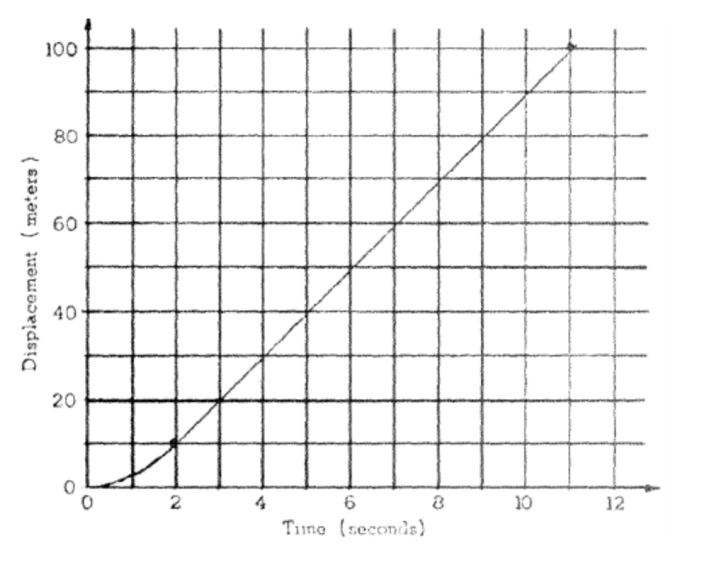
The first meters of a 100-meter dash are covered in 2 seconds by a sprinter who starts from rest and accelerates with a constant acceleration. The remaining 90 meters are run with the same velocity the sprinter had after 2 seconds.
a. Determine the sprinter’s constant acceleration during the first 2 seconds.
b. Determine the sprinters velocity after 2 seconds have elapsed.
c. Determine the total time needed to run the full 100 meters.
d. On the axes provided below, draw the displacement vs time curve for the sprinter.
▶️Answer/Explanation
Ans:
a. For the first 2 seconds, while acceleration is constant, d = ½ at2 Substituting the given values d = 10 meters, t = 2 seconds gives a = 5 m/s2
b. The velocity after accelerating from rest for 2 seconds is given by v = at, so v = 10 m/s
c. The displacement, time, and constant velocity for the last 90 meters are related by d = vt.
To cover this distance takes t = d/v = 9 s. The total time is therefore 9 + 2 = 11 seconds
d.