Question
A javelin thrower standing at rest holds the center of the javelin behind her head, then accelerates it through a distance of \(70 \mathrm{~cm}\) as she throws. She releases the javelin \(2.0 \mathrm{~m}\) above the ground traveling at an angle of \(30^{\circ}\) above the horizontal. Toprated javelin throwers do throw at about a \(30^{\circ}\) angle, not the \(45^{\circ}\) you might have expected, because the biomechanics of the arm allow them to throw the javelin much faster at \(30^{\circ}\) than they would be able to at \(45^{\circ}\). In this throw, the javelin hits the ground \(62 \mathrm{~m}\) away. What was the acceleration of the javelin during the throw? Assume that it has a constant acceleration.
▶️Answer/Explanation
Ans:
\(
\begin{aligned}
v_x & =v \cos 30^{\circ} \\
& \approx 0.86 v
\end{aligned}
\)
\(
\begin{aligned}
62 & =0.86 v t \\
t & =\frac{62}{0.86 v}
\end{aligned}
\)
The formula to calculate the vertical height \((y)\) travelled by the javelin before hitting the ground is given by
\[
y=v_y t-\frac{1}{2} g t^2 .
\]
Substitute 2 for \(y, 0.5 v\) for \(v_y,\left(\frac{62}{0.86 v}\right)\) for \(t\) and 9.80 for \(g\) into equation and solve to calculate the initial speed of the javelin.
\[
\begin{aligned}
2 & =0.5 v\left(\frac{62}{0.866 v}\right)-\frac{1}{2} \times 9.80 \times\left(\frac{62}{0.866 v}\right)^2 \\
2 & =36-\frac{25115.6}{v^2} \\
\frac{25115.6}{v^2} & =36-2 \\
v^2 & =\frac{25115.6}{34} \\
v & =\sqrt{\frac{25115.6}{34}} \\
& \approx 27.18
\end{aligned}
\]
The formula to calculate the horizontal distance \((d)\) travelled by the javelin thrower before throwing the javelin is given by
\[
v^2=u^2+2 a d \text {. }
\]
Here, \(u, a\) are the initial speed and the acceleration of the javelin thrower.
\(27.18^2=0^2+2 a \times 0.7\)
\(
\begin{aligned}
a & =\frac{27.18^2}{1.4} \\
& \approx 527.6
\end{aligned}
\)
Question: (12 points, suggested time 25 minutes)
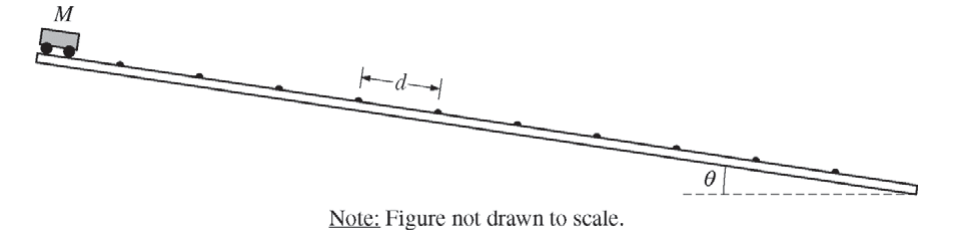
A long track, inclined at an angle θ to the horizontal, has small speed bumps on it. The bumps are evenly spaced a distance d apart, as shown in the figure above. The track is actually much longer than shown, with over 100 bumps. A cart of mass M is released from rest at the top of the track. A student notices that after reaching the 40th bump the cart’s average speed between successive bumps no longer increases, reaching a maximum value vavg . This means the time interval taken to move from one bump to the next bump becomes constant.
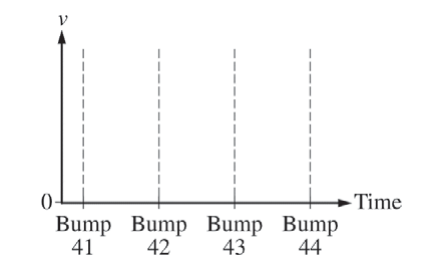
(a) Consider the cart’s motion between bump 41 and bump 44.
i. In the figure below, sketch a graph of the cart’s velocity v as a function of time from the moment it reaches bump 41 until the moment it reaches bump 44.
ii. Over the same time interval, draw a dashed horizontal line at v = vavg. Label this line “ vavg ”.
(b) Suppose the distance between the bumps is increased but everything else stays the same.
Is the maximum speed of the cart now greater than, less than, or the same as it was with the bumps closer together?
_______Greater than ________ Less than _________The same as
Briefly explain your reasoning.
(c) With the bumps returned to the original spacing, the track is tilted to a greater ramp angle θ . Is the maximum speed of the cart greater than, less than, or the same as it was when the ramp angle was smaller?
_________ Greater than __________ Less than ___________The same as
Briefly explain your reasoning.
(d) Before deriving an equation for a quantity such as vavg, it can be useful to come up with an equation that is intuitively expected to be true. That way, the derivation can be checked later to see if it makes sense physically. A student comes up with the following equation for the cart’s maximum average speed: vavg = \(C\frac{Mgsin\theta }{d}\), where C is a positive constant.
i. To test the equation, the student rolls a cart down the long track with speed bumps many times in front of a motion detector. The student varies the mass M of the cart with each trial but keeps everything else the same. The graph shown below is the student’s plot of the data for vavg as a function of M.
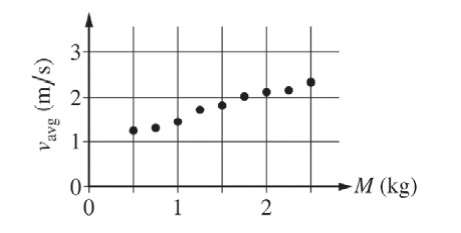
Are these data consistent with the student’s equation?
_________Yes ________No
Briefly explain your reasoning.
ii. Another student suggests that whether or not the data above are consistent with the equation, the equation could be incorrect for other reasons. Does the equation make physical sense?
_________Yes ____________ No
Briefly explain your reasoning.
▶️Answer/Explanation
Ans:
(a)
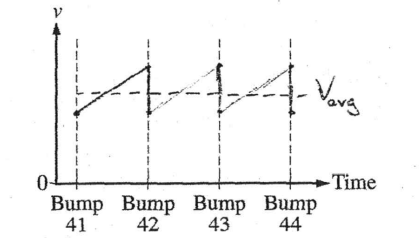
(b)
√ Greater than
Since cart will travel a greater distance there will be more time for the cart to accelerate ergo it will be able to attain a higher speed.
(c)
√ Greater than
With a greater angle more of the gravitational force will be directed in the same direction as the motion of the cart ergo increasing the carts acceleration along the ramps allowing the cart to reach a higher speed.
(d)
i.
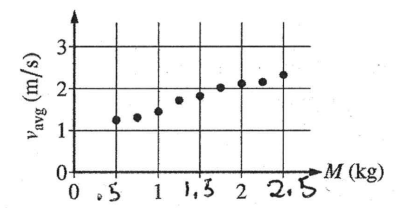
√ No
With the given equation one would expect that when the mass is doubled the vavg would double but that isn’t the case with the graph. From, 5 kg to 1 kg mass is doubled but not vavg.
ii.
√ No
One would expect that by increasing of the distance between bumps, vavg would also increase however the given equation suggests the opposite, It (equation) suggests that to increase vavg one could shorten of (distance between bumps), but that makes no physical sense because the bumps slow down the cart so one would want to increase the distance between bumps to increase vavg not decrease the distance.
Question
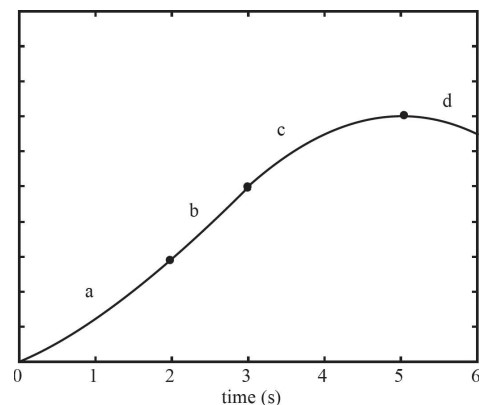
The motion of an object is given by the following velocity-versus-time graph.
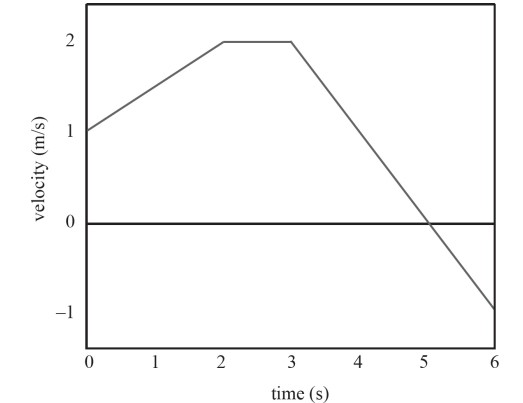
(a) What is the displacement of the object from time t = 0 s to t = 6 s in the graph above?
(b) At what times is the speed of the object increasing?
(c) Make of a sketch of the object’s position-versus-time graph during the time interval of t = 0 s to t = 6 s. Assume that the car begins at x = 0.
▶️Answer/Explanation
Ans:
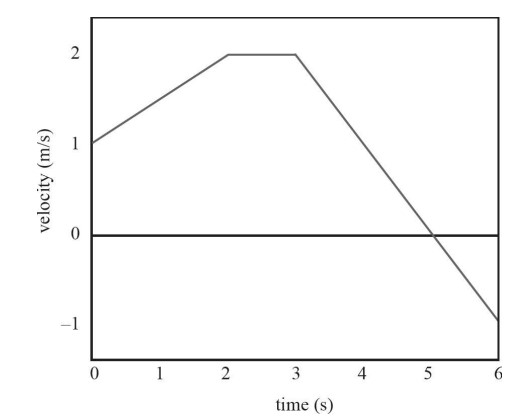
(a) On a velocity-versus-time graph, the displacement is the area between the graph and the x-axis. Area above the x-axis is positive displacement and area below the x-axis is negative displacement. The displacement from time t = 0 s to t = 6 s can be evaluated as
t = 0 s to t = 2 s: (2 s)(1 m/s) + \(\frac{1}{2}\)(2 s)(1 m/s) = 3 m
t = 2 s to t = 3 s: (1 s)(2 m/s) = 2 m
t = 3 s to t = 4 s: (1 s)(1 m/s) + \(\frac{1}{2}\)(1 s)(1 m/s) = 1.5 m
t = 4 s to t = 5 s: \(\frac{1}{2}\)(1 s)(1 m/s) = 0.5 m
t = 5 s to t = 6 s: \(\frac{1}{2}\)(1 s)(−1 m/s) = −0.5 m
The total displacement from time t = 2 s to t = 6 s is: 3 m + 2 m + 1.5 m + 0.5 m − 0.5 m = 6.5 m.
(b) The speed of the object is increasing when the magnitude of the velocity is increasing. This occurs from time t = 0 s to t = 2 s and t = 5 s to t = 6 s.
(c) 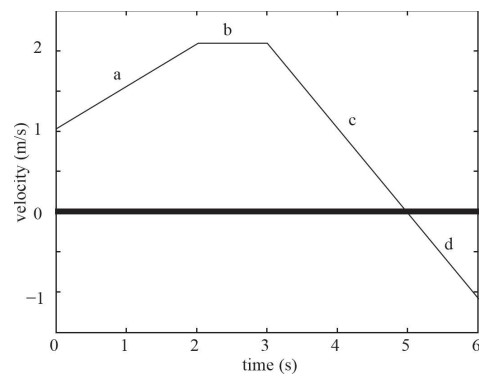
Section a tells you the object is speeding up in the positive direction (parabola with an increasingly steeper slope). Section b tells you the object is traveling with constant speed in the positive direction (linear line). Section c tells you the object is slowing down but still moving in the positive direction (parabola with a decreasingly steeper slope). Section d tells you the object is moving in the negative direction and speeding up (parabola with an increasingly steeper slope).