Question
A race car with a weight of \(1,709.94 \mathrm{~N}\) moves at a constant \(3.41 \mathrm{~m} / \mathrm{s}^{\wedge} 2\) while experiencing \(425.78 \mathrm{~N}\) worth of friction. What force must the engine be providing the car?
▶️Answer/Explanation
Ans:
\(\begin{aligned} & w=1709.94 \\ & a=3.41 \text { m/s^2 } \\ & \text { friction }=425.78 \mathrm{~N} \\ & \text { Force }- \text { Friction }=\mathrm{ma} \\ & \text { Force }-425.78=\left(\frac{w}{g}\right) a \\ & \text { Force }=425.78+\frac{1709.94}{9.8} \times 3.41 \\ & F=425.78+594.98 \\ & F=1020.77~N\end{aligned}\)Question
A massless tray is placed on an inclined plane with an angle of incline of θ. There is a coefficient of static friction \(\mu _{s}\) between the inclined plane and the massless tray. The tray is attached to a box of mass M by the pulley system shown below.
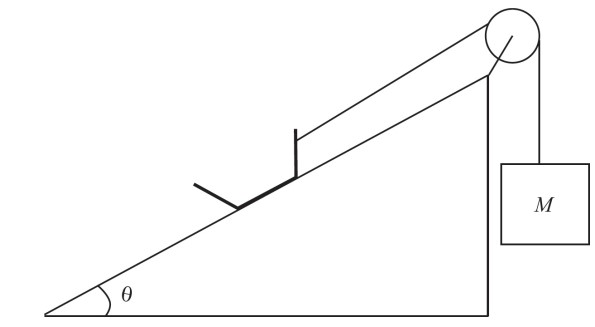
(a) If mass can be loaded onto the massless tray, how much mass m has to be loaded to stop the tray from being pulled up the inclined plane by M?
(b) How much mass m has to be loaded until the tray starts sliding down the inclined plane?
(c) If \(\mu _{k}\) = 0.3 and θ = 45°, what is the acceleration of the massless tray if m = 4M?
▶️Answer/Explanation
Ans:
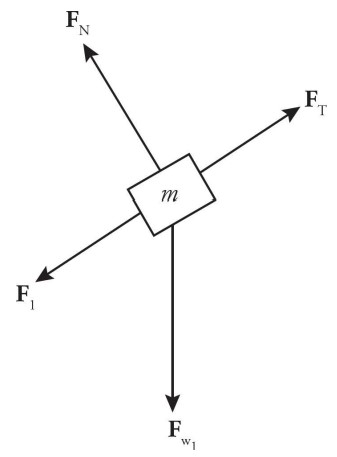
(a) The forces acting on the m mass are \(F _{T}\) (the tension in the string connecting it to M mass), \(F _{w}\) (the weight of the mass m), \(F _{N}\) (the normal force exerted by the inclined plane), and \(F _{f}\) (the force of static friction).
The forces acting on the M mass are \(F _{T}\) (the tension in the string connecting it to the m mass) and \(F _{w}\) (the weight of the block).
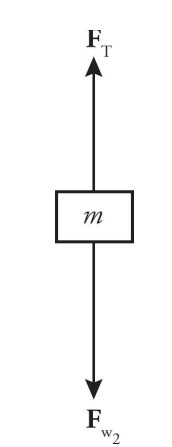
In order to stop the tray from moving, the net force on both the M mass and the mass m loaded on the tray must be zero. Newton’s First Law applied to the M mass yields
\(F_{w2}-F_{T}=0\Rightarrow F_{T}=F_{w2}=Mg\)
Newton’s First Law applied to the m yields
\(F_{T}-F_{g}-F_{f}=0\Rightarrow F_{T}-mg\sin (\theta)-\mu _{s}mg\cos (\theta )=0\)
Substituting \(F _{T}\) = Mg, you get
\(Mg-mg\sin \theta -\mu _{s}mg\cos \theta =0\)
\(mg\sin \theta +\mu _{s}mg\cos \theta =Mg\)
\(m=\frac{Mg}{g\sin \theta +\mu _{s}g\cos \theta}\)
(b) As the mass is trying to slide down the incline, the force of friction is acting in the opposite direction as in (a). There is no change to the M mass, so Newton’s First Law applied to the M mass still yields
\(F_{w2}-F_{T}=0\Rightarrow F_{T}=F_{w2}=Mg\)
Newton’s First Law applied to the m yields
\(F_{T}+F_{g}-F_{f}=0\Rightarrow F_{T}+mg\sin \theta -\mu _{s}mg\cos \theta =0\)
Substituting \(F _{T}\) = Mg, you get
\(Mg+mg\sin \theta -\mu _{s}mg\cos \theta =0\)
\(mg\sin \theta -\mu _{s}mg\cos \theta =Mg\)
\(m=\frac{Mg}{g\sin \theta +\mu _{s}g\cos \theta }\)
In order for the massless tray to start sliding down the inclined plane, m has to be greater than \(\frac{Mg}{g\sin \theta +\mu _{s}g\cos \theta }\).
(c) Newton’s First Law applied to the M mass yields
\(F_{T}-F_{w2}=Ma\Rightarrow F_{T}=F_{w2}+Ma\Rightarrow F_{T}=Mg+Ma\)
Newton’s First Law applied to the m yields
\(F_{g}-F_{f}-F_{T}=ma\Rightarrow mg\sin \theta -\mu _{k}mg\cos \theta -F_{T}=ma\)
Substituting \(F _{T}\) = Mg + Ma, you get

Plugging in m = 4M, θ = 45°, and\(\mu _{k}\) = 0.3, you get
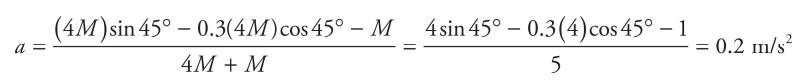
Question
A small box of mass m is placed on an inclined plane with an angle of incline of θ. There is a coefficient of kinetic friction \(\mu _{k}\) between the inclined plane and the small box. The small box is attached to a much heavier box of mass 3m by a pulley system shown below.
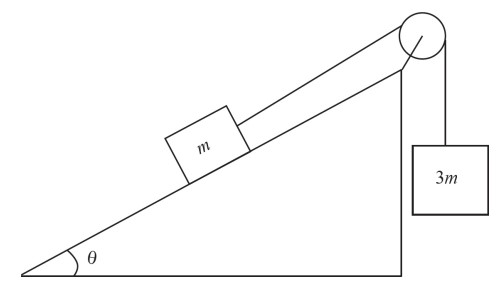
(a) Draw free body diagrams of both masses, including all of the forces acting on each.
(b) Assuming a frictionless, massless pulley, determine the acceleration of the blocks once they are released from rest in terms of \(\mu _{k}\), g, and θ.
(c) If \(\mu _{k}\) = 0.3 and θ = 45°, what distance is traveled by the blocks 3 s after being released from rest?
▶️Answer/Explanation
Ans:
(a) The forces acting on the small m mass are \(F _{T}\) (the tension in the string connecting it to the 3m block), \(F _{w}\) (the weight of the block), \(F _{N}\) (the normal force exerted by the inclined plane), and \(F _{f}\) (the force of kinetic friction).
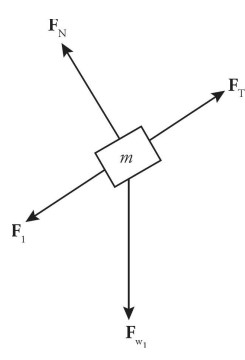
The forces acting on the larger 3m mass are \(F _{T}\) (the tension in the string connecting it to the m block) and \(F _{w}\) (the weight of the block).
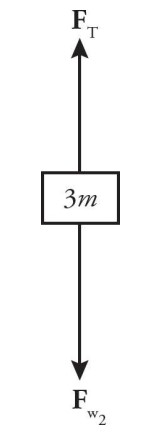
(b) Newton’s Second Law applied to the 3m mass yields
\(F_{w2}-F_{T}=3ma\Rightarrow 3mg-F_{T}=3ma\)
Newton’s Second Law applied to the m yields
\(F_{T}-F_{f}-F_{N}=ma\Rightarrow F_{T}-\mu _{k}mg\sin \theta -mg\cos \theta\)
Adding these two equations together, you find that
\(3mg-\mu _{k} mg\sin \theta -mg\cos \theta =ma+3ma\)
\(3mg-\mu _{k} mg\sin \theta -mg\cos \theta =4ma\)
\(a=\frac{3g-\mu _{k}g\sin \theta -\cos \theta }{4}\)
(c) Plugging in g = 10 m/\(s^{2}\), θ = 45°, and \(\mu _{k}\) = 1.0, the acceleration can be calculated as follows:
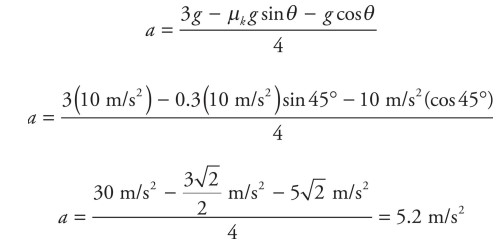
Apply Big Five #3:
\( d=v_{0}t+\frac{1}{2}at^{2}\Rightarrow d=0+\frac{1}{2}(5.2m/s)^{2}=23.4m\)
