Question
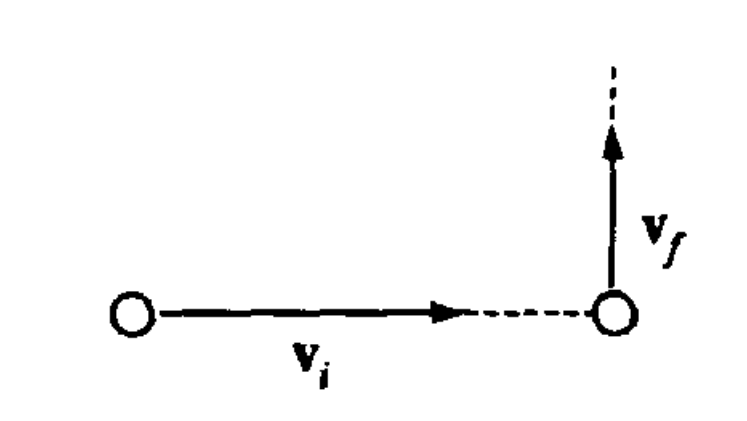
A ball initially moves horizontally with velocity vi, as shown above. It is then struck by a stick. After leaving the stick, the ball moves vertically with a velocity vf, which is smaller in magnitude than vi. Which of the following vectors best represents the direction of the average force that the stick exerts on the ball?

▶️Answer/Explanation
Ans:B
Solution: The direction of the force is the same as the direction of the acceleration, which is proportional to Δv = vf + (–vi)
Question
If vector A = 5î + 3ĵ, which of the following vectors B would the magnitude of the vector sum of A + B be equal to \(\sqrt{37}\)? Select two answers.
(A) B = −4î + 3ĵ
(B) B = î − 3ĵ
(C) B = −6î − 9ĵ
(D) B = î + 3ĵ
▶️Answer/Explanation
Ans:A, C
The components of the vector sum A + B = C must satisfy the equation: \(C=\sqrt{37}=\sqrt{(Cx)^{2}+(Cy)^{2}}\)
The only answer choices that satisfy the equation are (A):
A + B = C
\(A+B=(5-4)\breve{i}+(3+3)\breve{j}=\breve{i}+6\breve{j}=C\)
\(C=\sqrt{37}=\sqrt{(1)^{2}+(6)^{2}}\)
and (C): A + B = C
\( A+B=(5-6)\breve{i}+(3-9)\breve{j}=-\breve{i}-6\breve{j}=C\)
\(C=\sqrt{37}=\sqrt{(-1)^{2}+(-6)^{2}}\)
Questions (a)–(c) refer to the following scenario:
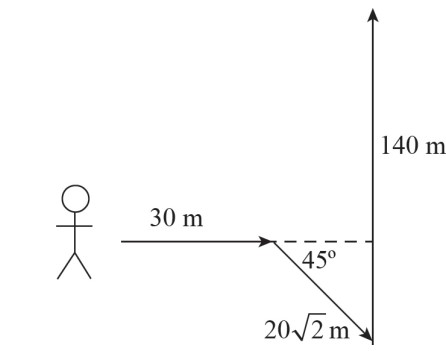
An explorer travels 30 m east, then 20\(\sqrt{2}\) m in a direction 45° south of east, and then 140 m north.
Question(a)
What is the distance traveled by the explorer?
(A) 167.2 m
(B) 169 m
(C) 170 m
(D) 198.2 m
▶️Answer/Explanation
Ans:D
The total distance traveled is equal to the sum of the individual distances traveled by the explorer: d = 30 m + 20\(\sqrt{2}\) m + 140 m = 198.2 m.
Question(b)
What is the displacement of the explorer?
(A) 130 m
(B) 169 m
(C) 170 m
(D) 215 m
▶️Answer/Explanation
Ans:A
The displacement is equal to the change in position of the explorer. The horizontal and vertical components of the explorer’s displacement can be calculated as follows:
Δx = 30 m + 20 cos45° = 50 m
Δy = −20 sin45° + 140 m = 120 m
The displacement of the explorer then is the magnitude of the vector (50i + 120j) m:
\(\Delta s=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}=\sqrt{(50m)^{2}+(120m)^{2}}=130m\)
Question(c)
The explorer took 60 s, 130 s, and 70 s to travel the 30 m, 20\(\sqrt{2}\) m, and 140 m north distances, respectively. What is the average velocity of the explorer over the total distance traveled?
(A) 0.50 m/s
(B) 33.3 m/min
(C) 0.76 m/s
(D) 100 m/min
▶️Answer/Explanation
Ans:A
As the displacement of the explorer was 130 m, the average velocity of the explorer is equal to

