Question
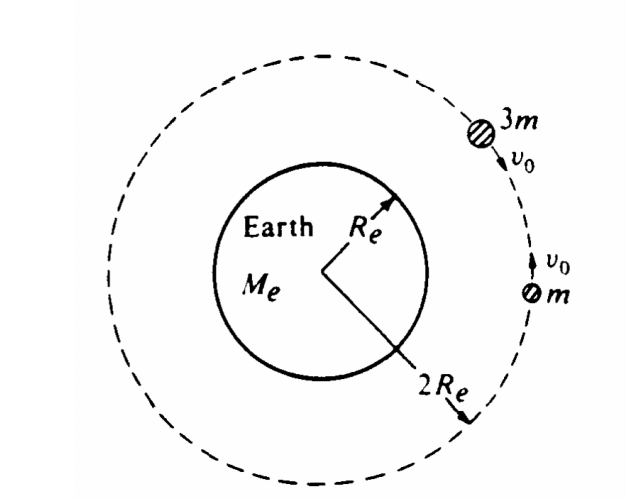
Two satellites, of masses m and 3m, respectively, are in the same circular orbit about the Earth’s center, as shown in the diagram above. The Earth has mass Me and radius Re. In this orbit, which has a radius of 2Re, the satellites initially move with the same orbital speed vo but in opposite directions.
a. Calculate the orbital speed vo of the satellites in terms of G, Me, and Re.
b. Assume that the satellites collide head-on and stick together. In terms of vo find the speed v of the combination immediately after the collision.
c. Calculate the total mechanical energy of the system immediately after the collision in terms of G, m, Me, and Re. Assume that the gravitational potential energy of an object is defined to be zero at an infinite distance from the Earth.
▶️Answer/Explanation
Ans:
a. Fg = Fc gives \(\frac{GM_{e}m}{(2R_{e})^{2}} = \frac{mv^{2}}{2R_{e}}\) giving v = \(|\frac{\overline{GM_{e}}}{\overline{2R_{e}}}\)
b. conservation of momentum gives (3m)v0 – mv0 = (4m)v’ giving v’ = ½ v0
c. E = PE + KE = \(-\frac{GM_{e}(4m)}{2R_{e}}+\left ( \frac{1}{2}(4m)v^{2} \right )= – \frac{2GM_{e}m}{R_{e}}+2m\left ( \frac{1}{2} |\frac{\overline{GM_{e}}}{\overline{2R_{e}}}\right )^{2} = – \frac{7GM_{e}m}{4R_{e}}\)
Question
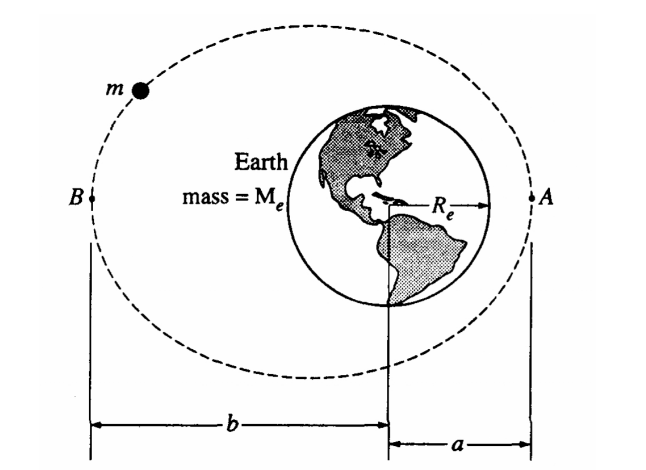
A spacecraft of mass 1,000 kilograms is in an elliptical orbit about the Earth, as shown above. At point A the spacecraft is at a distance rA = 1.2 × 107 meters from the center of the Earth and its velocity, of magnitude vA = 7.1 × 103 meters per second, is perpendicular to the line connecting the center of the Earth to the spacecraft. The mass and radius of the Earth are ME = 6.0 × 1024 kilograms and rE = 6.4 × 106 meters, respectively.
Determine each of the following for the spacecraft when it is at point A .
a. The total mechanical energy of the spacecraft, assuming that the gravitational potential energy is zero at an infinite distance from the Earth.
b. The magnitude of the angular momentum of the spacecraft about the center of the Earth.
Later the spacecraft is at point B on the exact opposite side of the orbit at a distance rB = 3.6 × 107 meters from the center of the Earth.
c. Determine the speed vB of the spacecraft at point B.
Suppose that a different spacecraft is at point A, a distance rA = 1.2 × 107 meters from the center of the Earth. Determine each of the following.
d. The speed of the spacecraft if it is in a circular orbit around the Earth
e. The minimum speed of the spacecraft at point A if it is to escape completely from the
▶️Answer/Explanation
Ans:
a. E = PE + KE = – \(\frac{GMm}{R}+ \frac{1}{2}mv^{2}= -8.1 \times 10^{9}J\)
b. L = mvr = 8.5 × 1013 kg-m2/s
c. Angular momentum is conserved so mvara = mvbrb giving vb = 2.4 × 103 m/s
d. Fg = Fc gives \(\frac{GMm}{R^{2}} = \frac{mv^{2}}{R}\) and v = \(|\frac{\overline{GM}}{R}\) = 5.8 × 103 m/s
e. Escape occurs when E = PE + KE = 0 giving \(- \frac{GMm}{R}+\frac{1}{2}mv^{2} = 0\) and vsec = \(|\frac{\overline{2GM}}{R}\) = 8.2 × 103 m/s
