Question
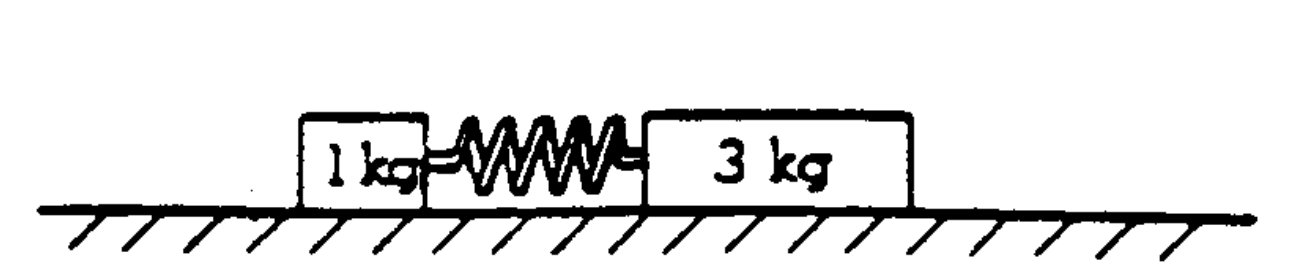
A massless spring is between a 1-kilogram mass and a 3-kilogram mass as shown above, but is not attached to either mass. Both masses are on a horizontal frictionless table. In an experiment, the 1-kilogram mass is held in place and the spring is compressed by pushing on the 3-kilogram mass. The 3-kilogram mass is then released and moves off with a speed of 10 meters per second.
a. Determine the minimum work needed to compress the spring in this experiment.
In a different experiment, the spring is compressed again exactly as above, but this time both masses are released simultaneously and each mass moves off separately at unknown speeds.
b. Determine the final velocity of each mass relative to the cable after the masses are released.
▶️Answer/Explanation
Ans:
a) The work to compress the spring would be equal to the amount of spring energy it possessed after compression.
After releasing the mass, energy is conserved and the spring energy totally becomes kinetic energy so the
kinetic energy of the mass when leaving the spring equals the amount of work done to compress the spring
W = ½ m v2 = ½ (3) (10)2 = 150 J
b) Apply momentum conservation to the explosion
pbefore = 0 = pafter 0 = m1v1f + m2v2f 0 = (1)v1f + (3)v2f v1f = 3 v2f
Apply energy conservation … all of the spring energy is converted into the kinetic energy of the masses
150 J = K1 + K2 150 = ½ m v1f2 + ½ m v2f2 sub in above for v2f
150 = ½ (1)(3v2f)2 + ½ (3)(v2f)2 v2f = 5 m/s v1f = 15 m/s
Question

A 2-kilogram block initially hangs at rest at the end of two 1-meter strings of negligible mass as shown on the left diagram above. A 0.003-kilogram bullet, moving horizontally with a speed of 1000 meters per second, strikes the block and becomes embedded in it. After the collision, the bullet/ block combination swings upward, but does not rotate.
a. Calculate the speed v of the bullet/ block combination just after the collision.
b. Calculate the ratio of the initial kinetic energy of the bullet to the kinetic energy of the bullet/ block combination immediately after the collision.
c. Calculate the maximum vertical height above the initial rest position reached by the bullet/block combination.
▶️Answer/Explanation
Ans:
a) Apply momentum conservation perfect inelastic. pbefore = pafter m1v1i = (m+M)vf vf = 1.5 m/s
b) KEi / KEf ½ m v1i2/ ½ (m+M)vf2 = 667
c) Apply conservation of energy of combined masses K = U ½ (m+M)v2 = (m+M)gh h = 0.11 m
Question

As shown above, a 0.20-kilogram mass is sliding on a horizontal, frictionless air track with a speed of 3.0 meters per second when it instantaneously hits and sticks to a 1.3-kilogram mass initially at rest on the track. The 1.3-kilogram mass is connected to one end of a massless spring, which has a spring constant of 100 newtons per meter. The other end of the spring is fixed.
a. Determine the following for the 0.20-kilogram mass immediately before the impact.
i. Its linear momentum ii. Its kinetic energy
b. Determine the following for the combined masses immediately after the impact.
i. The linear momentum ii. The kinetic energy
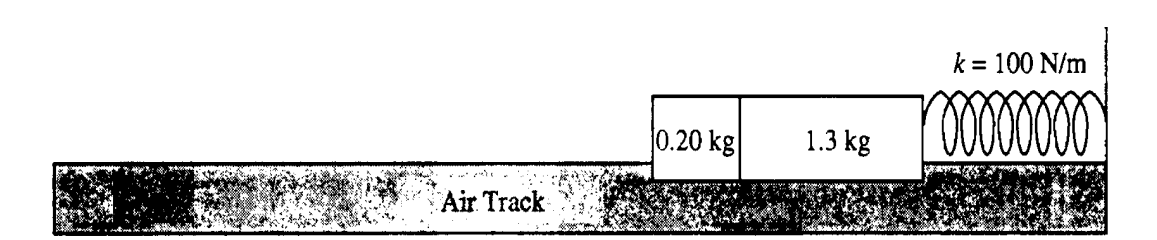
After the collision, the two masses compress the spring as shown.
c. Determine the maximum compression distance of the spring.
▶️Answer/Explanation
Ans:
a) i) p = mv = (0.2)(3) = 0.6 kg m/s
ii) K = ½ mv2 = ½ (0.2)(3)2 = 0.9 J
b) i.) Apply momentum conservation pbefore = pafter = 0.6 kg m/s
ii) First find the velocity after using the momentum above
0.6 = (1.3+0.2) vf vf = 0.4 m/s K = ½ (m1+m2) vf2 = ½ (1.3+0.2)(0.4)2 = 0.12 J
c) Apply energy conservation K = Usp 0.12 J = ½ k∆x2 = ½ (100) ∆x2 ∆x = 0.05 m
