Question: (7 points, suggested time 13 minutes)
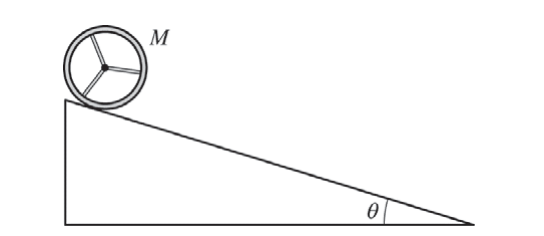
A wooden wheel of mass M, consisting of a rim with spokes, rolls down a ramp that makes an angle θ with the horizontal, as shown above. The ramp exerts a force of static friction on the wheel so that the wheel rolls without slipping.
(a)
i. On the diagram below, draw and label the forces (not components) that act on the wheel as it rolls down the ramp, which is indicated by the dashed line. To clearly indicate at which point on the wheel each force is exerted, draw each force as a distinct arrow starting on, and pointing away from, the point at which the force is exerted. The lengths of the arrows need not indicate the relative magnitudes of the forces.
ii. As the wheel rolls down the ramp, which force causes a change in the angular velocity of the wheel with respect to its center of mass?
Briefly explain your reasoning.
(b) For this ramp angle, the force of friction exerted on the wheel is less than the maximum possible static friction force. Instead, the magnitude of the force of static friction exerted on the wheel is 40 percent of the magnitude of the force or force component directed opposite to the force of friction. Derive an expression for the linear acceleration of the wheel’s center of mass in terms of M, θ, and physical constants, as appropriate.
(c) In a second experiment on the same ramp, a block of ice, also with mass M, is released from rest at the same instant the wheel is released from rest, and from the same height. The block slides down the ramp with negligible friction.
i. Which object, if either, reaches the bottom of the ramp with the greatest speed?
________Wheel ________Block _________Neither; both reach the bottom with the same speed.
Briefly explain your answer, reasoning in terms of forces.
ii. Briefly explain your answer again, now reasoning in terms of energy.
▶️Answer/Explanation
Ans:
(a) (i)
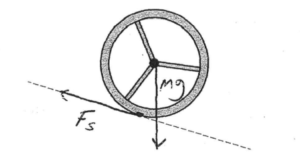
(ii)
The fork of static friction.
Briefly explain your reasoning.
The static friction force is being applied at a point at a radius with respect to the enter of mass, causing a torque and subsequent change in angular velocity.
(b) \(\sum F = \frac{ma}{m} = \frac{Mgsin\Theta – 0.4 Mgsin\Theta }{M}\)
a = 0.6 gsh
(c)
i. _X_ Block
The block only has a single force acting upon it gravity. The wheel has two gravity and friction, which is opposing the downward motion. Since friction is slowing the wheel down, the block of ice will roach the bottom of this range with the greatest speed.
ii.
All of the block’s gravitational potential energy is being converted directly into linear kinetic energy. The wheel’s GPE is being converted into both linear kinetic energy and rotational kinetic energy. Since both objects have the some starting GPE, the block will reach the bottom with the greatest velocity because all of its GPE is being converted to linear KE.
Question: (7 points, suggested time 13 minutes)
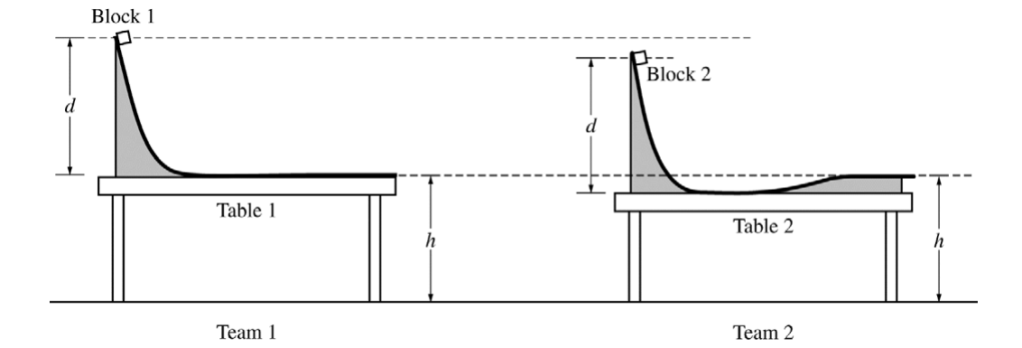
A physics class is asked to design a low-friction slide that will launch a block horizontally from the top of a lab table. Teams 1 and 2 assemble the slides shown above and use identical blocks 1 and 2, respectively. Both slides start at the same height d above the tabletop. However, team 2’s table is lower than team 1’s table. To compensate for the lower table, team 2 constructs the right end of the slide to rise above the tabletop so that the block leaves the slide horizontally at the same height h above the floor as does team 1’s block (see figure above).
(a) Both blocks are released from rest at the top of their respective slides. Do block 1 and block 2 land the same distance from their respective tables?
____ Yes ____ No
Justify your answer.
In another experiment, teams 1 and 2 use tables and low-friction slides with the same height. However, the two slides have different shapes, as shown below.
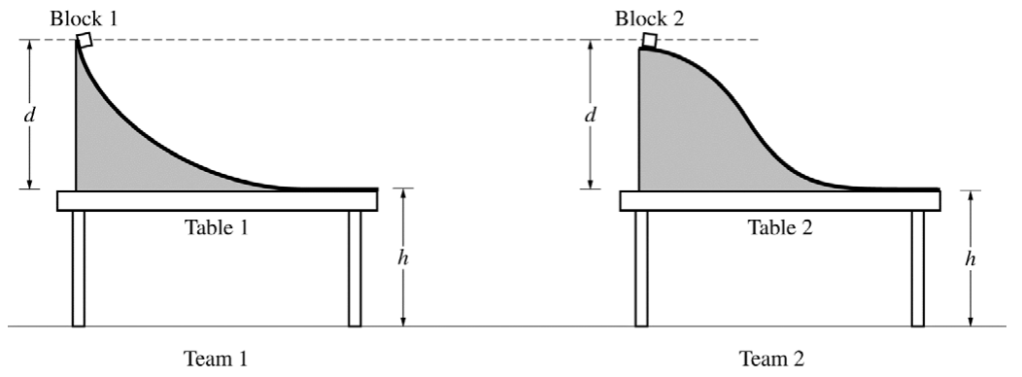
(b) Both blocks are released from rest at the top of their respective slides at the same time.
i. Which block, if either, lands farther from its respective table?
____ Block 1 ____ Block 2 ____ The two blocks land the same distance from their respective tables.
Briefly explain your reasoning without manipulating equations.
ii. Which block, if either, hits the floor first?
____ Block 1 ____ Block 2 ____ The two blocks hit the floor at the same time.
Briefly explain your reasoning without manipulating equations.
▶️Answer/Explanation
Ans:
√ No
For team I, all of the block’s potential energy, gets converted into kinetic energy. This is also true for team 2, However with team 2, the block has less initial potential energy than team t, b/c it travels a shorter not vertical distance to therefore it has less kinetic energy at height h. This results in less velocity at height h for team so a shorter distance travelled b/c both blocks are in the air for the same amount of time.
(b)
i. √ The two blocks land the same distance from their respective tables.
Even though the slides have different heights, the changes in height are the same so they have the same potential energy at the start, and kinetic energy at the and, since they launch from the same height h, they are in the air for the same amount of time and go the same distance.
ii. √ Block 1
Block 1 travels a shorter horizontal distance on the table before reaching its maximum speed than block 2. This means it reaches the end of the table before block 2 and hits the ground first because they are in the air for the same amount of time.
Question: (7 points, suggested time 13 minutes)
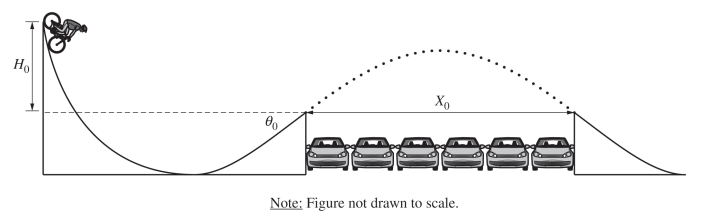
A stunt cyclist builds a ramp that will allow the cyclist to coast down the ramp and jump over several parked cars, as shown above. To test the ramp, the cyclist starts from rest at the top of the ramp, then leaves the ramp, jumps over six cars, and lands on a second ramp.
H0 is the vertical distance between the top of the first ramp and the launch point.
q0 is the angle of the ramp at the launch point from the horizontal.
X0 is the horizontal distance traveled while the cyclist and bicycle are in the air.
m0 is the combined mass of the stunt cyclist and bicycle.
(a) Derive an expression for the distance X0 in terms of H0, q0, m0, and physical constants, as appropriate.
(b) If the vertical distance between the top of the first ramp and the launch point were 2H0 instead of H0, with no other changes to the first ramp, what is the maximum number of cars that the stunt cyclist could jump over? Justify your answer, using the expression you derived in part (a).
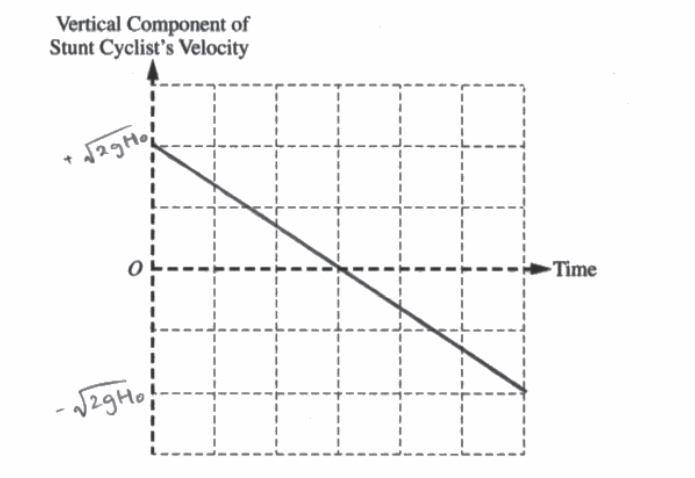
(c) On the axes below, sketch a graph of the vertical component of the stunt cyclist’s velocity as a function of time from immediately after the cyclist leaves the ramp to immediately before the cyclist lands on the second ramp. On the vertical axis, clearly indicate the initial and final vertical velocity components in terms of H0, q0, m0, and physical constants, as appropriate. Take the positive direction to be upward.
▶️Answer/Explanation
Ans:
(a)
\(\sum E_{i} =\sum E_{f}\)
\(m_{0}gH_{0} = \frac{1}{2}m_{0}{v_{0}}^{2}\)
\({v_{0}}^{2} = 2gH_{0}\)
\(v_{0} = \sqrt{2gH_{0}}\)
\(vertical x_{0} = \frac{1}{2}at^{2} + v_{0}sin\theta _{0}t\)
\(o = \frac{1}{2}at + v_{0}sin\theta \)
\(o = \frac{1}{2}(-9.8)t + v_{0}sin\theta \)
\(t = \frac{v_{0}sin\theta}{4.9} = \frac{\sqrt{2gH_{0}sin\theta }}{4.9}\)
\(horizontal: x = vt\)
\(x_{0} = \sqrt{2gH_{0}}. \frac{\sqrt{2gH_{0}}sin\theta }{4.9}\)
\(x_{0} =\frac{2gH_{0}sin\theta _{0}}{4.9}\)
(b)
The cyclist would be able to jump over 12 cars. In the expression in part (a), X0 × H0, so if H0 doubles, then X0 doubles as well. Double the amount of 6 cars (X0) is 12 Cars.
(c)