Question
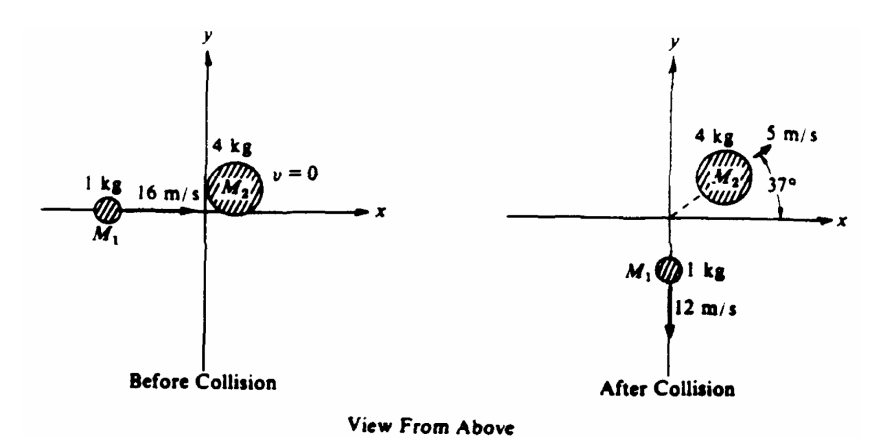
Two objects of masses Ml = 1 kilogram and M2 = 4 kilograms are free to slide on a horizontal frictionless surface. The objects collide and the magnitudes and directions of the velocities of the two objects before and after the collision are shown on the diagram above. (sin 37° = 0.6, cos 37° = 0.8, tan 37º = 0.75)
a. Calculate the x and y components (px and py, respectively) of the momenta of the two objects before and after the collision, and write your results in the proper places in the following table.
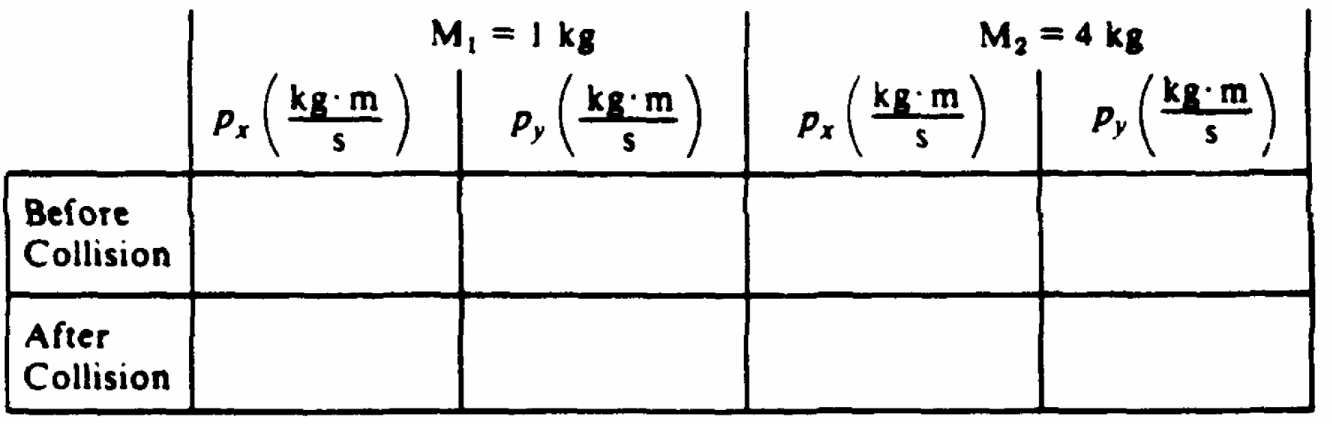
b. Show, using the data that you listed in the table, that linear momentum is conserved in this collision.
c. Calculate the kinetic energy of the two-object system before and after the collision.
d. Is kinetic energy conserved in the collision?
▶️Answer/Explanation
Ans:
a) Before the collision there is only an x direction momentum of mass M1 … px = m1v1x = 16, all the rest are 0
After the collision, M1 has y direction momentum = m1v1fy = 12 and M2 has x and y direction momentums.
Using trig to find the x and y velocities of mass M2 … vx = 5 cos 37 = 3, and vy = 5 sin 37 = 3.75.
Then plug into mv to get each x and y momentum after.
| M1 = 1 kg | M2 = 4 kg | |||
| px (kg m /s) | py (kg m /s) | px (kg m /s) | py (kg m /s) | |
| Before | 16 | 0 | 0 | 0 |
| After | 0 | -12 | 16 | 12 |
b) SUM = 16 -12 16 12
When adding x’s before they = x’s after 16=16, when adding y’s before they equal y’s after |-12|=12
c) Kinetic Energy Before Kinetic Energy After
K = ½ m1v1ix2 K = ½ m1v1fy2 + ½ m2v22
K = ½ (1)(16)2 = 128 J K = ½ (1)(12)2 + ½ (4)(5)2 = 122 J
d) From above, K is not conserved.
Question
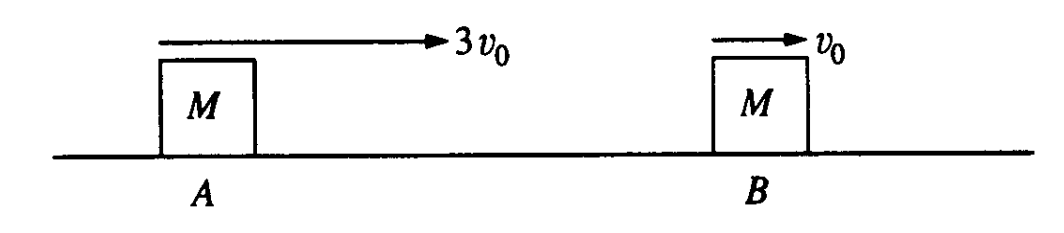
Two identical objects A and B of mass M move on a one-dimensional, horizontal air track. Object B initially moves to the right with speed vo. Object A initially moves to the right with speed 3vo, so that it collides
with object B. Friction is negligible. Express your answers to the following in terms of M and vo.
a. Determine the total momentum of the system of the two objects.
b. A student predicts that the collision will be totally inelastic (the objects stick together on collision). Assuming this is true, determine the following for the two objects immediately after the collision.
i. The speed
ii. The direction of motion (left or right)
When the experiment is performed, the student is surprised to observe that the objects separate after the collision and that object B subsequently moves to the right with a speed 2.5vo.
c. Determine the following for object A immediately after the collision.
i. The speed
ii. The direction of motion (left or right)
d. Determine the kinetic energy dissipated in the actual experiment.
▶️Answer/Explanation
Ans:
a) ptot = M(3vo) + (M)(vo) = 4mvo
b) i) Apply momentum conservation perfect inelastic. pbefore = pafter
4Mvo = (m1+m2)vf 4Mvo = (2M) vf vf = 2vo
ii) Since they are both moving right they would have to be moving right after
c) i) Apply momentum conservation pbefore = pafter
4Mvo = m1v1f + m2v2i 4Mvo = Mvaf + M(2.5vo) vaf = 1.5 vo
ii) As before, the would have to be moving right.
d) ∆K = Kf – Ki = (½ mavaf2 + ½ mbvbf2) – ( ½ mavai2 + ½ mbvbi2) = 4.25 Mvo2 – 5 Mvo2 = – 0.75 Mvo2
Question
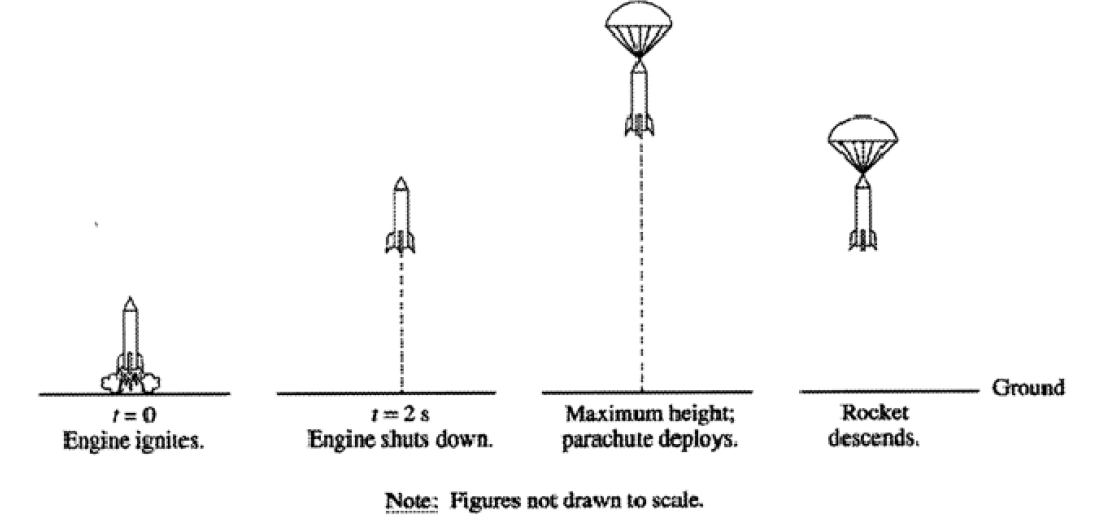
A model rocket of mass 0.250 kg is launched vertically with an engine that is ignited at time t = 0, as shown above. The engine provides an impulse of 20.0 N•s by firing for 2.0 s. Upon reaching its maximum height, the rocket deploys a parachute, and then descends vertically to the ground.
(a) On the figures below, draw and label a free-body diagram for the rocket during each of the following intervals.

(b) Determine the magnitude of the average acceleration of the rocket during the 2 s firing of the engine.
(c) What maximum height will the rocket reach?
(d) At what time after t = 0 will the maximum height be reached?
▶️Answer/Explanation
Ans:
a) 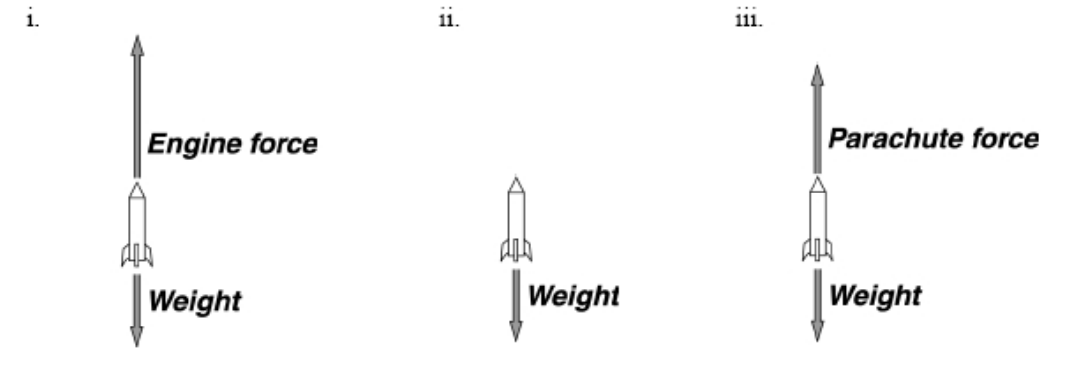
b) Jengine = Feng t (20) = Feng (2) Feng = 10 N
Fnet = ma (Feng–mg)=ma (10 – 0.25(9.8))=(0.25)a a = 30 m/s2
c) Find distance traveled in part (i) d1 =vit + ½ a t2 = 0 + ½ (30)(2)2 = 60 m
Find distance in part (ii) free fall.
first find velocity at end of part (i) = vi for part ii then find distance traveled in part ii
v1f = v1i + a1t1 = (0) + (30)(2) = 60 m/s v2f2 = v2i2+2gd2 = (60)2 + 2(–9.8)(d2) d2 = 184 m
dtotal = 244 m
d) Find time in part ii. v2f = v2i + gt 0 = 60 + –9.8 t t = 6.1 s
then add it to the part I time (2 s) total time → 8.1 sec