Question
An object is moving to the west at a constant speed. Three forces are exerted on the object. One force is \(10 \mathrm{~N}\) directed due north, and another is \(10 \mathrm{~N}\) directed due west. What is the magnitude and direction of the third force if the object is to continue moving to the west at a constant speed?
(A) \(10 \sqrt{3} \mathrm{~N}\), directed northwest
(B) \(10 \sqrt{3} \mathrm{~N}\), directed southeast
(C) \(10 \sqrt{2} \mathrm{~N}\), directed northwest
(D) \(10 \sqrt{2} \mathrm{~N}\), directed southeast
▶️Answer/Explanation
Ans:D
Question
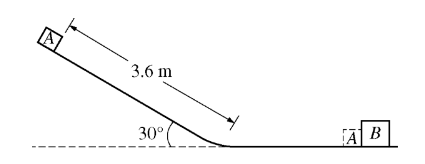
Block \(A\) of mass \(2.0 \mathrm{~kg}\) is released from rest at the top of a \(3.6 \mathrm{~m}\) long plane inclined at an angle of \(30^{\circ}\), as shown in the figure above. After sliding on the horizontal surface, block \(A\) hits and sticks to block \(B\), which is at rest and has mass \(3.0 \mathrm{~kg}\). Assume friction is negligible. The speed of the blocks after the collision is most nearly
(A) \(2.4 \mathrm{~m} / \mathrm{s}\)
(B) \(3.2 \mathrm{~m} / \mathrm{s}\)
(C) \(3.8 \mathrm{~m} / \mathrm{s}\)
(D) \(6.0 \mathrm{~m} / \mathrm{s}\)
▶️Answer/Explanation
Ans:A
Question
A 1-kilogram object is moving to the right with a velocity of 6 meters per second. It collides with and sticks to a 2-kilogram mass, which is also moving to the right, with a velocity of 3 meters per second. What happens to the total kinetic energy during this collision?
(A) The kinetic energy is conserved because the collision is elastic.
(B) The kinetic energy is conserved even though the collision is not elastic.
(C) Some kinetic energy is lost during the collision even though total momentum is conserved.
(D) Some kinetic energy is lost during the collision because of the elastic nature of the collision.
▶️Answer/Explanation
Ans:(C) Momentum is always conserved. However, kinetic energy is lost unless the collision is elastic, in which case the kinetic energy is also conserved:
\(p_{i}=1(+6)+2(3)=12kg m/s=p_{f}=3v_{f}\)
\(v_{f} =\) 4 m/s
Initial KE: \((\frac{1}{2})(1)(6)^{2}+(\frac{1}{2})(2)(3)^{2}=27J\)
Final KE: \((\frac{1}{2})(3)(4)^{2}=24J\)
3 joules are lost.
Questions (a) and (b) refer to the information below:
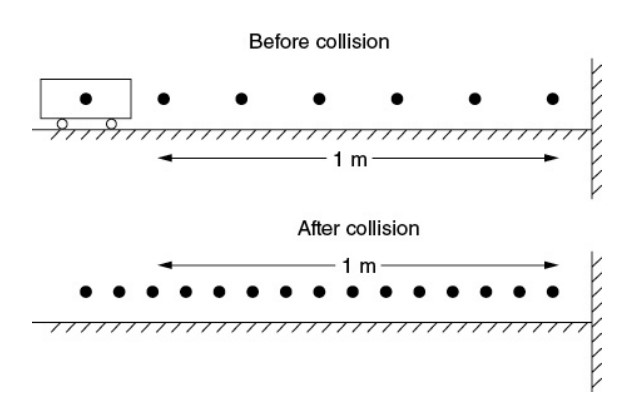
In the laboratory, a 0.5-kg cart collides with a fixed wall, as shown in the preceding diagram. The collision is recorded with a video camera that takes 20 frames per second. A student analyzes the video, placing a dot at the center of mass of the cart in each frame. The analysis is shown above.
Question(a)
About how fast was the cart moving before the collision?
(A) 0.25 m/s
(B) 4.0 m/s
(C) 0.20 m/s
(D) 5.0 m/s
▶️Answer/Explanation
Ans:
B—The dots divide the 1-meter distance into five parts. In the time between dots, the cart travels 1/5 of a meter, or 0.2 m. The time between dots is 1/20 of a second, or 0.05 s. At constant speed, the speed is given by distance/time: 0.20 m/0.05 s = 4 m/s.
Question(b)
Which of the following best estimates the change in the cart’s momentum during the collision?
(A) 27 N∙s
(B) 13 N∙s
(C) 1.3 N∙s
(D) 2.7 N∙s
▶️Answer/Explanation
Ans:
D—Initially, the cart’s mass is 0.5 kg and speed is 4 m/s, so the cart’s momentum is mv = 2 N∙s. In the collision, the cart loses that 2 N∙s in order to stop briefly and then gains more momentum in order to speed up again. So the momentum change must be more than 2 N∙s. How much more? After collision, the cart is moving slower than 4 m/s because the dots are closer together, so the cart’s momentum is less than 2 N∙s. The cart’s momentum change is (2 N∙s) + (something less than 2 N∙s); the only possible answer is 2.7 N∙s.
Question
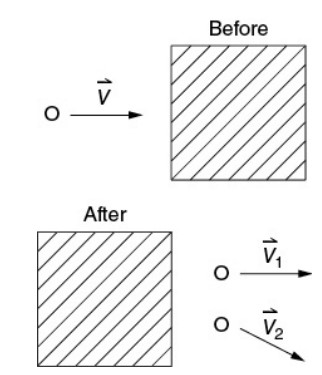
In an experiment, a marble rolls to the right at speed v, as shown in the top diagram. The marble rolls under a canopy, where it is heard to collide with marbles that were not initially moving. Such a collision is known to be elastic. After the collision, two equal-mass marbles are observed leaving the canopy with velocity vectors \(\vec{v_{1}} and \vec{v_{2}}\) directed as shown. Which of the following statements justifies why the experimenter believes that a third marble was involved in the collision under the canopy?
(A) Before collision, the only marble momentum was directed to the right. After the collision, the combined momentum of the two visible marbles is still to the right. Another marble must have a leftward momentum component to conserve momentum.
(B) Before collision, the only marble momentum was directed to the right. After the collision, the combined momentum of the two visible marbles has a downward component; another marble must have an upward momentum component to conserve momentum.
(C) Before collision, the only marble kinetic energy was directed to the right. After the collision, the combined kinetic energy of the two visible marbles is still to the right. Another marble must have a leftward kinetic energy component to conserve kinetic energy.
(D) Before collision, the only marble kinetic energy was directed to the right. After the collision, the combined kinetic energy of the two visible marbles has a downward component; another marble must have an upward kinetic energy component to conserve kinetic energy.
▶️Answer/Explanation
Ans:
B—Choices C and D are wrong because kinetic energy doesn’t have a direction. Choice A is wrong because momentum conservation does not require a leftward momentum component—since the initial momentum was all to the right, the final momentum should be to the right. It’s the vertical momentum that’s the problem. Since the vertical momentum was zero to start with, any vertical momentum after collision must cancel out.
