Question
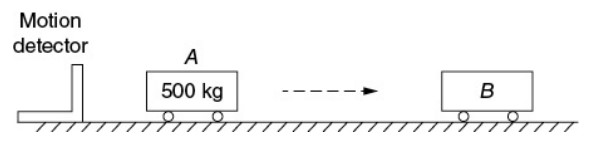
In Experiment 1, two carts collide on a negligible-friction track: Cart A with mass 500 g, and Cart B with unknown mass. Before the collision, Cart B is at rest. Adhesive is attached to the carts such that after the collision, the carts stick together. The speeds of Cart A before collision and after collision are measured using the sonic motion detector, as shown in the diagram.
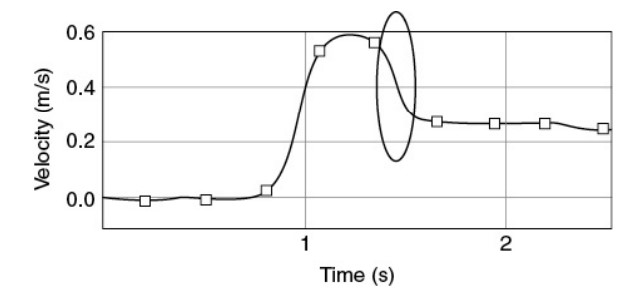
(a) In one trial, the motion detector is turned on, Cart A is given a shove, the carts collide, and then the detector is turned off. The detector produces the velocity-time graph shown as follows. On the graph, indicate with a circle the portion of the graph that represents the collision occurring. Explain how you figured this out.
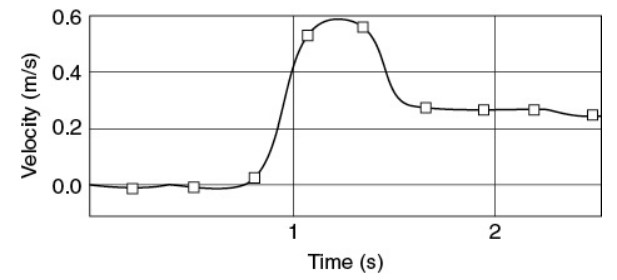
(i) Use the graph to estimate the speed of Cart A before the collision.
(ii) Use the graph to estimate the speed of Cart A after the collision.
(b) In numerous trials, the speeds of Cart A before and after the collision are measured. You are asked to construct a graph of this data whose slope can be used to calculate the mass of Cart B.
(i) What should you graph on each axis?
(ii) Explain in several sentences how you will use the slope of this graph to calculate the mass of Cart B. Be specific both about the calculations you will perform, and about why those calculations will produce the mass of Cart B.
(c) In Experiment 2, the adhesive is removed such that the carts bounce off of one another. The motion detector is again positioned to read the speed of Cart A before and after collision.
(i) Describe an experimental procedure by which the speed of Cart B after collision can be measured. You may use any equipment available in your physics laboratory, but you may not use a second sonic motion detector.
(ii) The masses of Carts A and B are now both known; the speeds of both carts before and after collision have been measured. Explain how you could determine whether the collision in Experiment 2 was elastic. Be sure to describe specifically the calculations you would perform, as well as how you would use the results of those calculations to make the determination.
▶️Answer/Explanation
Ans:
Conservation of momentum means the total momentum before the collision equals the total momentum after the collision. Before the collision, the total momentum is that of Cart \(A:m_{A}v_{A}\). After the collision, the total momentum is \((m_{A}+m_{B}){v}’\) where v′ is the speed of Cart A (and, because they stick together, the speed of Cart B, too). Set these momentum expressions equal: \(m_{A}v_{A}=(m_{A}+m_{B}){v}’\).
This equation can be solved for the y-axis variable divided by the x-axis variable: \(\frac{v_{A}}{{v}’}=\frac{(m_{A}+m_{B})}{m_{A}}\)
So, to get the mass of Cart B, I’d determine the slope of the line on the graph, and set that equal to \(\frac{(m_{A}+m_{B})}{m_{A}}\). The mass of Cart A is given as 500 g, so I’d plug that in and solve for \(m_{B}\).
Three ideas occur, but many are possible:
• Measure the distance that Cart B has to travel to the end of the track. When the carts collide, start a stopwatch; when Cart B hits the end of the track, stop the stopwatch. The speed of Cart B is the distance you measured divided by the time on the stopwatch.
• After the collision, when the detector has already read the speed of Cart A but before Cart B reaches the end of the track, lift up Cart A. Now the detector can read Cart B’s speed.
• Let Cart B roll off the end of the track and fall to the floor as a projectile. Measure the vertical height y of the track off the ground; the time t that the cart was in the air is given by \(y=1/2gt^{2}\), where g is 10 m/s per second. Measure the horizontal distance from the track’s edge to the spot where the cart landed. Then the speed of the cart is this horizontal distance divided by the calculated time of flight.
“Elastic” means that the total kinetic energy of the two carts was the same before and after collision. Before the collision, the only kinetic energy is that of Cart A: \(1/2m_{A}v_{A}^{2}\). After the collision, the total kinetic energy is the sum of the kinetic energy of both carts, where each cart’s kinetic energy is given by \(1/2mv^{2}\). Compare the total kinetic energy after collision to Cart A’s kinetic energy before collision. If these values are equal, the collision was elastic. If the kinetic energy after the collision is less than the kinetic energy before collision, the collision was not elastic.
Question
A long-distance, unmanned probe is sent to another planet. To keep it oriented correctly, the probe is given a lot of spin during the early part of the trip. However, when the probe is getting close to its destination, the spin is no longer desired. Two very long cables with mass at the end of each are extended while the probe is still in
deep space. Once extended, the cables are released and the probe begins its landing sequence.
(a) Explain qualitatively why the spinning will help the probe oriented correctly. Describe the underlying physics concepts using equations and diagrams as needed.
(b) Explain what is accomplished by the action of extending and releasing the cables near the end of the probe’s flight. Describe the underlying physics concepts using equations and diagrams as needed. Do the masses need to be a significant portion of the probe’s mass for this procedure to be effective?
(c) What happens to all of the probe’s linear momentum when it lands on its destination planet? Describe qualitatively in terms of physics principles what happens during the landing.
▶️Answer/Explanation
Ans:
(a) The spinning probe acts as a gyroscope since angular momentum is both a vector and conserved. The direction of the angular momentum requires an external torque to be changed. Therefore, barring some outside force, the probe will maintain the orientation it has when the angular velocity is given to its moment of inertia: \(L=I\omega\)
(b) By extending the masses outward from the probe’s body, the moment of inertia of the spinning probe can be greatly increased. Note that the masses need not be that great in order to change the moment of inertia substantially as the distance, R , from the axis of rotation can be made quite large by using a long cable and the R term is squared in the moment of inertia calculation: \(I=mR^{2}\)
Increasing the moment of inertia serves to slow the spin rate of the probe by decreasing the angular velocity in order to conserve angular momentum: \(L=I_{small}\omega=I_{large}\omega _{small}\)
(c) Linear momentum ( mv ) of the probe-planet system must be conserved. Equal and opposite impulses ( FΔt ) are delivered to the probe and the planet during impact. However, because of their vastly different masses, what is a major impulse to the probe turns out to be a moderate impulse to the entire planet and has almost no perceptible effect on the planet’s motion:
\(M_{probe}\Delta V_{big}-M_{big}\Delta V_{small}=0\)
Question
Two blocks, Block A of mass m and Block B of mass 2m, are attached together by a spring. The blocks are free to move on a level, frictionless surface. The spring is compressed and then the blocks are released from rest. Consider two different systems. One system consists only of Block A; the other system consists of both blocks and the connecting spring. In a clear, coherent, paragraph-length response, explain whether kinetic energy, total mechanical energy, and/or linear momentum is conserved in each of the systems described.
▶️Answer/Explanation
Ans:
The paragraph response must discuss kinetic energy, total mechanical energy, and linear momentum for each of the two systems. For example:
In system A, kinetic energy is not conserved. When the blocks are released, Block A speeds up away from Block B. Kinetic energy depends on mass and speed only. Since Block A’s speed increases without changing its mass, kinetic energy cannot remain constant. In system A, total mechanical energy is not conserved. Since the system consists only of Block A, there is no interaction with another object that would allow for the storage of potential energy. The force of the spring on Block A would be a force external to the system, and the spring does work on Block A because Block A moves parallel to the spring force; when a net force external to the system does work, mechanical energy is not conserved. In system A, linear momentum is not conserved. Either the reasoning for system A’s kinetic energy or total mechanical energy can be extended here. Linear momentum depends on mass and speed, and Block A’s speed changes without changing mass. Or, the spring force is external to the system, and momentum is only conserved in systems on which no net external force acts.
In system B, kinetic energy is not conserved. Kinetic energy is a scalar, so kinetic energy of a system of objects is just the addition of the kinetic energies of all the objects in the system. Both blocks speed up, so both blocks are increasing their kinetic energy, increasing the system’s kinetic energy. In system B, total mechanical energy is conserved. No force external to the spring-blocks system does work, so mechanical energy is conserved. The kinetic energy gained by the blocks was converted from potential energy stored in the spring. In system B, linear momentum is conserved. No force external to the spring-blocks
system acts, so linear momentum is conserved. Here even though Block B gains linear momentum, momentum is a vector—its gain of momentum is canceled by the momentum gained by Block A in the opposite direction.
