Question
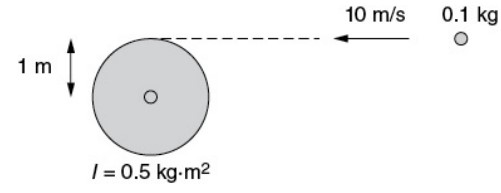
A disk of radius 1 m and rotational inertia I = 0.5 kg.m2 is free to rotate, but initially at rest. A blob of putty with mass 0.1 kg is traveling toward the disk with a speed of 10 m/s, as shown in the preceding figure. The putty collides with the outermost portion of the disk and sticks to the disk. What is the angular momentum of the combined disk-putty system after the collision?
(A) 5 \(kg\cdot m^{2}/s\)
(B) 1 \(kg\cdot m^{2}/s\)
(C) 0.5 \(kg\cdot m^{2}/s\)
(D)0 \(kg\cdot m^{2}/s\)
▶️Answer/Explanation
Ans:
B—In a collision, momentum—including angular momentum—is conserved. The question might as well be asking, “What is the angular momentum of the two objects before the collision?” And since the disk is at rest initially, the question is asking the even easier question, “What is the angular momentum of the putty before collision?” The axis of rotation is the center of the disk. The putty is a point mass; the angular momentum of a point mass is mvr with r the distance of closest approach to the axis. That’s (0.1 kg)(10 m/s)(1 m) = 1 \(kg\cdot m^{2}/s\).
Question

Three wagons each have the same total mass (including that of the wheels) and four wheels, but the wheels are differently styled. The structure, mass, and radius of each wagon’s wheels are shown in the preceding chart. In order to accelerate each wagon from rest to a speed of 10 m/s, which wagon requires the greatest energy input?
(A) Wagon A
(B) Wagon B
(C) Wagon C
(D) All require the same energy input
▶️Answer/Explanation
Ans:A
The energy input must be enough to change the translational kinetic energy of the cart and to change the rotational kinetic energy of the wheels. Since the wheels are all of the same radius, they will rotate with the same angular speed when the wagon reaches 10 m/s. Whichever wheels have the largest rotational inertia will therefore require the largest energy input to get to the same speed. Calculating, wagon A has the largest rotational inertia of 0.0025 \(kg\cdot m^{2}\).
Question
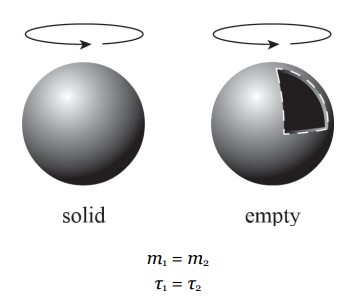
Two spheres of equal size and equal mass are rotated with an equal amount of torque. One of the spheres is solid with its mass evenly distributed throughout its volume, and the other is hollow with all of its mass concentrated at the edges. Which sphere would rotate faster?
(A) Solid sphere
(B) Hollow sphere
(C) They would rotate at equal rates.
(D) Additional information is required to determine the relative rates of rotation.
▶️Answer/Explanation
Ans:A
You know \(T_{Net}=I\alpha\). The torque applied to each is equal, so the sphere with a smaller moment of inertia (I) will rotate more quickly. Moment of inertia is smaller for an object with its mass concentrated closer to the center, so the solid sphere will have a smaller moment of inertia and thus rotate faster.
Question
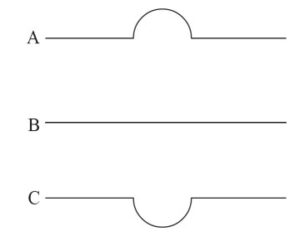
Three identical balls are rolled from left to right across the three tracks above with the same initial speed. Assuming the tracks all have negligible friction and the balls have enough initial speed to reach the ends of each track, which set correctly orders the average speed of the balls on the three tracks?
(A) A = B = C
(B) B > C > A
(C) C > B > A
(D) Cannot be determined
▶️Answer/Explanation
Ans:C
The correct answer is (C). For the left and right sides of the tracks, all three tracks are identical. Looking only at the middle segment of each track, (B) would hold steady throughout. Choice (A) would decrease the speed of the ball as it climbed the hill, then increase the speed back to the original amount as it descended the hill. That means it spends the entire segment at a speed less than the initial speed. Choice (C) would be the opposite of (A). The balls gains speed as it descends, and then loses speed as it climbs back up, eventually ending at the original speed. Therefore, it spends the entire middle segment at a speed greater than the initial amount.
Question
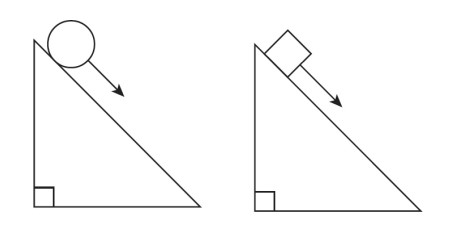
Two objects, a sphere and a block of the same mass, are released from rest at the top of an inclined plane. The sphere rolls down the inclined plane without slipping. The block slides down the plane without friction. Which object reaches the bottom of the ramp first?
(A) The sphere, because it gains rotational kinetic energy, but the block does not
(B) The sphere, because it gains mechanical energy due to the torque exerted on it, but the block does not
(C) The block, because it does not lose mechanical energy due to friction, but the sphere does
(D) The block, because it does not gain rotational kinetic energy, but the sphere does
▶️Answer/Explanation
Ans:D
The energy is the same for both objects to go from the top of the incline to the bottom. With the sphere some of it will need to be rotational kinetic energy. The block has pure translational kinetic energy and will reach the bottom of the incline first.
