Question:(7 points, suggested time 13 minutes)
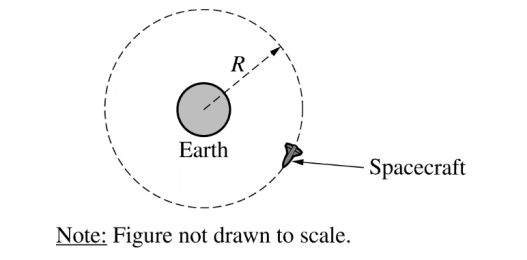
A spacecraft of mass m is in a clockwise circular orbit of radius R around Earth, as shown in the figure above. The mass of Earth is ME .
(a) In the figure below, draw and label the forces (not components) that act on the spacecraft. Each force must be represented by a distinct arrow starting on, and pointing away from, the spacecraft.
(b)
i. Derive an equation for the orbital period T of the spacecraft in terms of m, ME , R, and physical constants, as appropriate. If you need to draw anything other than what you have shown in part (a) to assist in your solution, use the space below. Do NOT add anything to the figure in part (a).
ii. A second spacecraft of mass 2m is placed in a circular orbit with the same radius R. Is the orbital period of the second spacecraft greater than, less than, or equal to the orbital period of the first spacecraft?
____ Greater than ____ Less than ____ Equal to
Briefly explain your reasoning.
(c) The first spacecraft is moved into a new circular orbit that has a radius greater than R, as shown in the figure below.
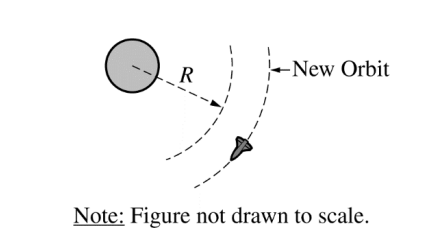
Is the speed of the spacecraft in the new orbit greater than, less than, or equal to the original speed?
____ Greater than ____ Less than ____ Equal to
Briefly explain your reasoning.
▶️Answer/Explanation
Ans:
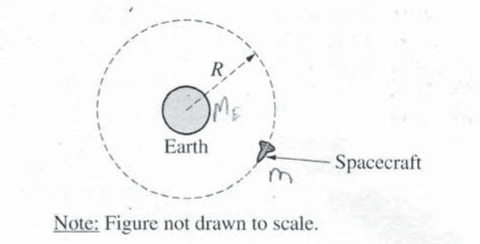
(a)
(b) (i)
\(\sum F = ma\)
Fg = ma
\(G\frac{mM_{E}}{r^{2}} = \frac{mv^{2}}{r}\)
\(\frac{GM_{E}}{r} = \left ( \frac{2\pi .r}{T} \right )^{2}\)
\(\frac{GM_{E}}{r} = \frac{4\pi ^{2}.r^{2}}{T^{2}}\)
\(T^{2} = \frac{4\pi ^{2}.r^{2}}{\left ( \frac{GM_{E}}{r} \right )}\)
\(\sqrt{T^{2}} = \sqrt{\frac{4\pi ^{2}.r^{3}}{GM_{E}}}\)
\(T = \sqrt{\frac{4\pi ^{2}.r^{3}}{GM_{E}}}\)
(ii)
× equal to
The orbital period of the second spacecraft is the same as the first because in the equation \(G\frac{mM_{E}}{r^{2}} = \frac{mv^{2}}{r}\) the mass of the spacecraft cancels on both sides of the equation, which means it does not affect the period. \(\binom{Not in euation }{T = \sqrt{\frac{4\pi ^{2}.r^{3}}{GM_{E}}}}\)
(c)
× less than
The speed of the spacecraft in the second orbit will be slower because in the equation \(G\frac{mM_{E}}{r^{2}} = \frac{mv^{2}}{r}\) , the m’s and r’s cancel and you get the equation \(\frac{GM_{E}}{r} =v ^{2}\) . In the second orbit, r increases and so the number or the left side of the equation is smaller, This means that V2 equals a smaller number than before, so therefore V decreases. (Speed decreases).
Question
A mass m is resting at a height h above the ground. When released, the mass can slide down a frictionless track to a loop-the-loop of radius R as shown below.
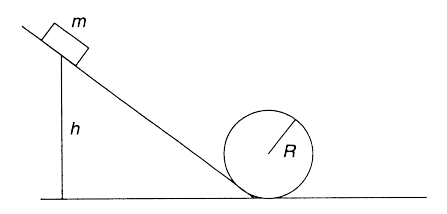
(a) As the mass slides down the incline, it gains speed. However, the mass may or may not “make it” around the loop without falling out. Why and under what conditions will the mass travel around the loop without falling out? Why and under what conditions will it not complete the loop? Explain your reasoning qualitatively, making sure you address the normal force experienced by the mass.
(b) Two fellow students are arguing about whether the maximum possible R of a loop that the mass can make it around will be linearly dependent on height h or if the relationship will be some power law. Without solving for the relationship explicitly, indicate a line of reasoning that would settle this argument.
(c) Within the loop, the normal force is always acting in a centripetal direction. Explain why the normal force is not always equal to mv2 / R at each point. Are there any points along the loop where the normal force is equal to mv2 / R ? Support your argument with free-body diagrams.
(d) If the minimum height h has been found for a fixed loop of size R but a rolling ball of mass m is substituted for the sliding mass, the ball will (indicate your choice):
_____ make it through the loop more easily
_____ pass through the loop the same as before
_____ fall out of the loop Justify your answer qualitatively, with no equations or calculations.
▶️Answer/Explanation
Ans:
2. (a) As the value h is raised, the mass gains velocity at the bottom of the incline. As the mass slides around the inside of the loop, it will lose speed as it goes back up. The entire time the mass is inside the loop, it must be undergoing centripetal acceleration (specifically, its v2 / R must equal its inward acceleration). If the mass is moving too slowly to maintain its circular motion, it will fail to complete the loop. The centripetal force is supplied by the normal force throughout the trajectory (sometimes also with or against the force of gravity). If the normal force goes to zero, this indicates a loss of contact between the sliding mass and the track. The slowest speed will occur at the top of the loop. Therefore, this is the most likely place for the mass to fall. At the top, gravity is acting centripetally along with the normal force, so Newton’s second law gives us:
N + mg = mv2/ R
As h gets smaller, the speed at the top will get smaller, which will decrease the right hand side of the equation above. At some point, mv2/ R will get as small as mg , at which point the normal force will be at zero. Any speed greater than this will let the mass complete the loop. Any speed lower than this will cause the mass to fail to complete the loop.
(b) The object has gravitational potential energy in the beginning, which is linearly proportional to h . Part of the potential energy is transformed into kinetic energy at the top of the loop. Kinetic energy is proportional to v2 . However, centripetal force is also proportional to v2 and the centripetal force is linear with respect to the normal force. It is this normal force going to zero that determines the critical speed. So the student who claims there is a linear dependence between h and R is correct.
(c) Because the normal force is not always the only centripetal force, it alone is not equal to mv2/ R . Generally speaking, a component of the force due to gravity is acting centripetally (top half of the loop) or centrifugally (bottom half of the loop). However, at the points halfway between the top and bottom, the normal force indeed is acting
alone centripetally and is equal to mv2/R . The following drawings show only the radial component of the two forces ( FN , FgR ).
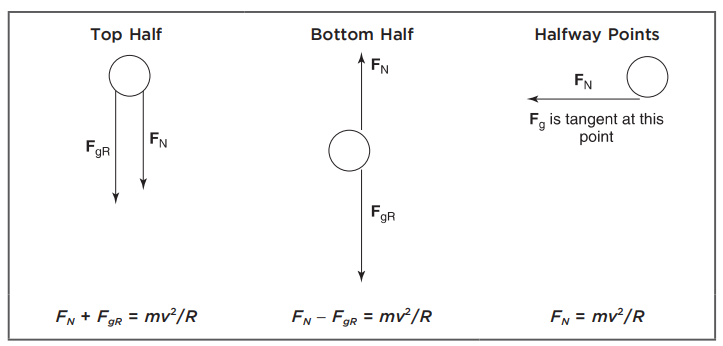
Tangent components of gravity speed up or slow down the object but do not participate in the centripetal acceleration.
(d) __X___ fall out of the loop Since the original gravitational potential energy must now be going into rotation kinetic energy, less energy will be available for the tangential speed needed to make it through the loop. Since the height, h, was set minimally for the sliding block, the rolling object will not have enough linear kinetic energy for its tangential speed to clear the top of the loop.
Question
A 2-kilogram mass is twirled in a vertical circle as shown. It is attached to a 2-meter rope. As the mass just clears the ground (point A ), its velocity is 10 m/s to the right. Neglect any air resistance. When the mass reaches point B , it makes a 30-degree angle to the horizontal as shown.
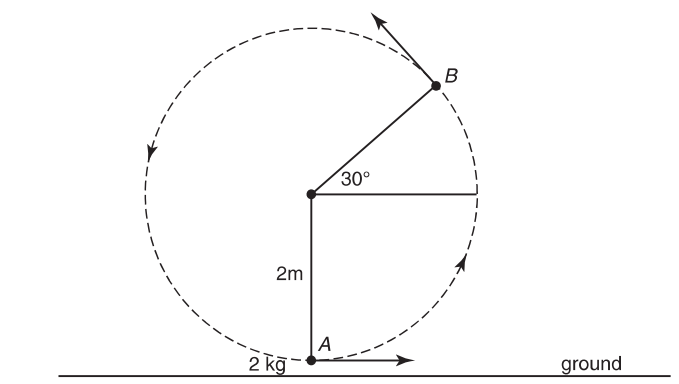
(a) Describe qualitatively, using words and diagrams, the difference in the object’s speed at point B if the twirling is done (i) at constant speed or (ii) at constant
tension. Which would result in the greater speed at point B ? Include an analysis of how the tension must change in part (i).
(b) At point B , the rope is released and the mass becomes a projectile. Assuming the rope has a uniform distribution of mass and remains attached to the flying object. Which of the following options best describe the projectile’s range as compared with a launch without the rope?
_____ addition of rope makes no difference to the range
_____ addition of rope increases the range
_____ addition of rope decreases the range
Explain your reasoning.
(c) When twirling the object at constant speed, explain in terms of work and energy, how the constant speed is maintained. Is the path truly circular when the object’s speed is maintained? In your explanation, be explicit about which forces are doing positive work and which are doing negative work.
▶️Answer/Explanation
(a) (i) To maintain constant speed, the tension must be constantly adjusted as the object undergoes its centripetal motion. The tension will be lower at point B than it is at the bottom as there is a component of gravity “helping” the tension in the centripetal direction (as opposed to gravity acting centrifugally at point A):
FcA = FcB = mv2/R
TA − mg = TB + mg sin 30° = mv2/R
TB = TA − mg(1 + sin 30°)
(ii) Constant tension will result in a much higher speed at point B as the tension will be locked in at TA above. Since the tension at point B will be higher than in
case (i), mv2/R must be greater as well. Constants m and R mean the speed must be increased.
(b) __X__ addition of rope decreases the range
Although we are ignoring air friction in this problem, we must consider the effect of the additional mass. Although free-fall problems generally ignore mass, the rope will have an effect on the effective launch velocity. The end of the rope directly attached to the twirling mass has the same velocity as the object. However, the rest of the distributed mass is moving at a lower velocity (down to zero at the center of the circle). Therefore, the net effect of the added mass will be to decrease the launch velocity. In addition, recall that the equations of motion actually track the center of mass of an object. Since the center of mass for the combined rope-plus-object system is lower (the mass of the rope extends below the 2 kg mass), the combined rope-plus object system is effectively being launched from a lower height. A lower launch velocity from a lower height will result in a shorter range for the projectile.
(c) While on the way up during the circular motion, the force due to gravity is doing negative work. The component of weight that is tangent does this negative work. Therefore to maintain the same kinetic energy, the tension must do some positive work. In order to accomplish this, the tension must supply an upward tangent component as well, i.e., the circle cannot be perfect. On the downward half of the circular motion, the positive and negative work roles of the tangent components of gravity and tension must reverse.
