Question: (12 points, suggested time 25 minutes)
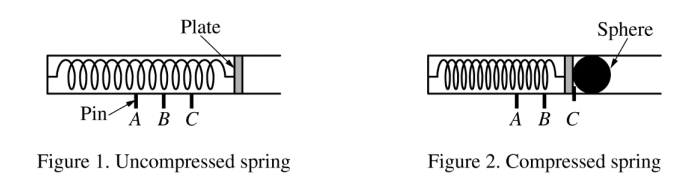
A projectile launcher consists of a spring with an attached plate, as shown in Figure 1. When the spring is compressed, the plate can be held in place by a pin at any of three positions A, B, or C. For example, Figure 2 shows a steel sphere placed against the plate, which is held in place by a pin at position C. The sphere is launched upon release of the pin. A student hypothesizes that the spring constant of the spring inside the launcher has the same value for different compression distances.
(a) The student plans to test the hypothesis by launching the sphere using the launcher.
i. State a basic physics principle or law the student could use in designing an experiment to test the hypothesis.
ii. Using the principle or law stated in part (a)(i), determine an expression for the spring constant in terms of quantities that can be obtained from measurements made with equipment usually found in a school physics laboratory.
(b) Design an experimental procedure to test the hypothesis in which the student uses the launcher to launch the sphere. Assume equipment usually found in a school physics laboratory is available.
In the table below, list the quantities and associated symbols that would be measured in your experiment. Also list the equipment that would be used to measure each quantity. You do not need to fill in every row. If you need additional rows, you may add them to the space just below the table.
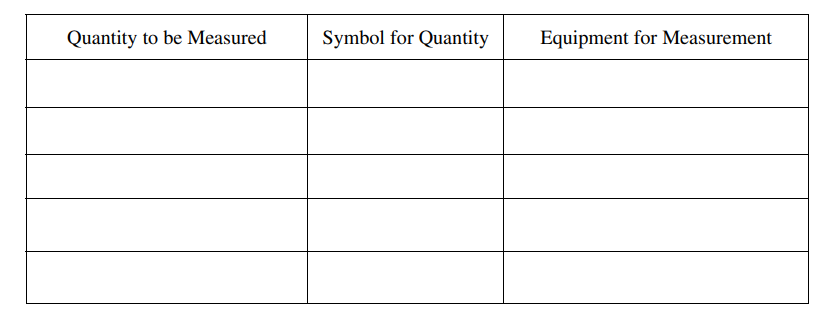
(b) Describe the overall procedure to be used to test the hypothesis that the spring constant of the spring inside the launcher has the same value for different compression distances, referring to the table. Provide enough detail so that another student could replicate the experiment, including any steps necessary to reduce experimental uncertainty. As needed, use the symbols defined in the table and/or include a simple diagram of the setup.
(c) Describe how the experimental data could be analyzed to confirm or disconfirm the hypothesis that the spring constant of the spring inside the launcher has the same value for different compression distances.
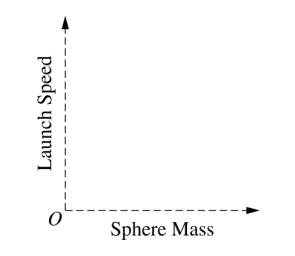
(d) Another student uses the launcher to consecutively launch several spheres that have the same diameter but different masses, one after another. Each sphere is launched from position A. Consider each sphere’s launch speed, which is the speed of the sphere at the instant it loses contact with the plate. On the axes below, sketch a graph of launch speed as a function of sphere mass.
▶️Answer/Explanation
Conservation of Energy
\(\frac{1}{2}kx^{2} = mgh\)
\(k = \frac{2mgh}{x}\)
(b)
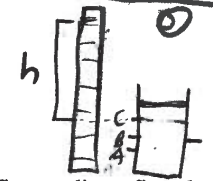
- First, use the ruler to measure the compression distance for the spring at each position (A,B,C) – this will be X. Also, measure the mass of the sphere, this will be m.
- Next, compress the spring to a chosen position, piece the pin, and load the sphere.
- Release the pin, and measure the maximum distance (h) that the ball travelling above its release point.
- Repeat the experiment (starting at step 2) multiple times at each position, and repeat it at each of the three positions.
Before ReleaseAfter Release

(c) First, the experiment should be repeats multiple times at each position to limit experimenter uncertainty. At each distance calculate the spring constant with the expression \(K = \frac{2mgh}{x} (ii),\) with the average height at that position as h, that measures mass of the sphere as M, and the measured very close at each of the positions, then the hypothesis is confirms, otherwise, it is disconfirmed.
(d)
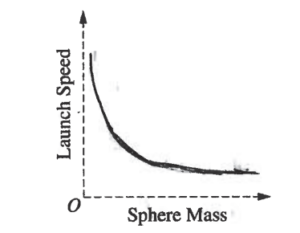
\(\frac{1}{2} kx^{2} = \frac{1}{2}mv^{2}\)
\(kx^{2} = mv^{2}\)
\(v^{2} = \frac{kx^{2}}{m}\)
\(v = \sqrt{\frac{kx^{2}}{m}}\) constant
\(v \alpha \frac{1}{\sqrt{m}}\) v
Question

In the diagram above, a spring-block system is oscillating on a flat horizontal surface. Part of the surface is frictionless, and part of the surface is not frictionless. The block starts at rest at position x = 0 cm. The block is then pushed to the left, compressing the spring, until it reaches the position x = –50 cm. After being pushed in, the block is released and allowed to move naturally.
(a) Draw a graph of the system’s position as a function of time starting from the moment it is released and explain your reasoning behind the graph you draw. Be sure to label important values on the graph.
(b) Given that the mass m = 2 kg and the spring constant k = 100 N/m, what is the magnitude of work done by the non-frictionless surface?
▶️Answer/Explanation
Ans:
(a) Your graph should look like this:
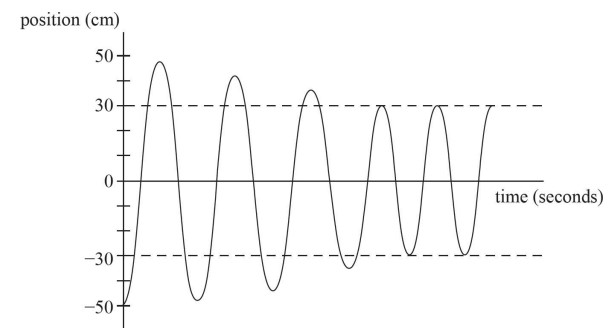
First, it must start at position –50 as the problem indicates. Second, it must go up to a point that is nearly 50 but not quite. This is because the frictional surface will remove some of the energy from the system as the block slides across it. Each time the block swings back to the frictional surface, it will drain a little more of the energy, making the amplitude slowly taper off until it eventually is only on the frictionless surface. Because the frictionless surface extends to 30 cm, it will oscillate between that point and –30 cm indefinitely.
(b) The energy of a spring system can be found by \(PE=\frac{1}{2}kA^{2}\), where A is the amplitude of the system, so the initial energy of the system will be \(PE=\frac{1}{2}(100)(0.5)^{2}=100/8=12.5J\). After the oscillations have tapered off, it will have a new energy of \(PE=\frac{1}{2}(100)(0.3)^{2}=45.5J\). Therefore, the frictional surface has caused 8 J of energy to be lost.
Question
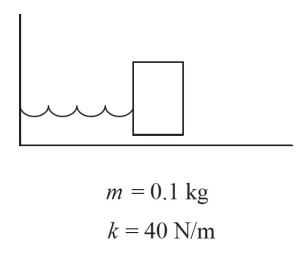
A horizontal spring with a force constant of 40 N/m is attached a 0.1 kg block.
(a) If the block is pulled to a distance of 0.5 m and released, what is the maximum speed of the block?
(b) What is the frequency of the oscillations?
(c) If the spring were flipped vertically and attached to the ground with the block placed on top, how would the natural length of the spring change?
(d) How does the frequency of the oscillations of the vertical spring-block oscillator compare with the frequency when it was placed horizontally?
▶️Answer/Explanation
Ans:
(a) When pulled to a distance of 0.5 m, the block has maximum potential energy given by the equation \(U=\frac{1}{2}kA^{2}\). All of this energy is converted to kinetic energy when the block reaches maximum speed:
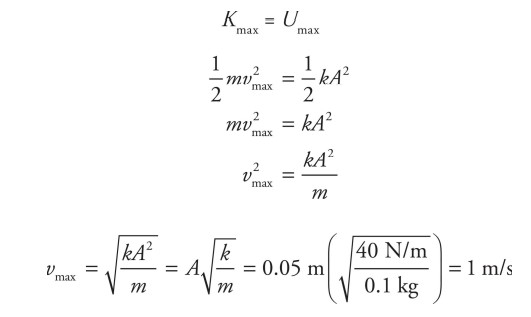
(b) The frequency of oscillations is given by the following equation:
\(f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=\frac{1}{2\pi }\sqrt{\frac{40N/m}{0.1kg}}=\frac{10}{\pi }Hz=3.2Hz\)
(c) When the spring is placed vertically on the ground with the block on top, there are two forces acting on the block at the new natural length: the weight of the block and the upwards restoring force. These two forces are equal to each other at the natural length:
\(F_{rest}=F_{g}\)
\(kx = mg\)
\(x=\frac{mg}{k}=\frac{(0.1kg)(10m/s^{2})}{40N/m}=0.025m\)
The natural length of the spring would decrease by 0.025 m
(d) The frequency of spring-block oscillator is given by the equation \(f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\). Flipping the spring vertically does not affect k or m, so the frequency of oscillations will remain unchanged.
